「固体物理の基礎 上・2 固体のバンド理論: アシュクロフト、マーミン」
内容紹介:
学部生にも大学院生にも使えるよう工夫され、内容の取捨選択がしやすく、種々の目的、異なる水準でもうまく使い分けられる。固体物理学の現象の記述と理論的解析による統一という著者の目標は完全に達成されている。1981年刊行、309ページ。
著者について:
ニール・W・アシュクロフト(ウィキペディア、経歴詳細)
イギリスの物理学者(固体物理学)、1938年生。1958年ニュージーランド大学卒業。学位は1964年ケンブリッジ大学。シカゴ大学およびコーネル大学で博士研究員、1975年教授。1990年にHorace White Professor of Physics。2006年名誉教授。
デヴィッド・マーミン(ウィキペディア、ホームページ)
コーネル大学名誉教授(物理学)。米国物理学会のリリエンフェルト賞および米国物理教育学会のクロプステッグ賞を受賞。米国科学アカデミー、米国芸術科学アカデミーの会員。この数十年の間に、量子論の基礎的な問題に関する多くの著作を執筆しており、科学の啓蒙に関する明瞭さと機知には定評がある。
訳者について:
松原武生(まつばらたけお)
1921-2014 昭和後期-平成時代の理論物理学者。
大正10年4月3日生まれ。北大教授をへて昭和30年京大教授となる。61年岡山理大教授。誘電体、超伝導、超流動などを研究。「温度グリーン関数」の概念を提案した。36年仁科記念賞。日本物理学会会長をつとめた。平成26年12月15日死去。93歳。大阪府出身。大阪帝大卒。著作に「超流動と超伝導」「固体物理学」など。
町田一成(まちだかずしげ)
1968年東京教育大学理学部卒業。1973年同上理学研究科博士課程修了。京都大学理学部助手、岡山大学理学部助教授、教授を経て、岡山大学大学院自然科学研究科教授。
理数系書籍のレビュー記事は本書で275冊目。
ようやく2冊目を読み終えた。このように精緻な教科書は読むのはとても根気がいる。
章立ては次のとおりだ。
第11章:バンド構造を計算する他の方法
第12章:電子の動力学の半古典的モデル
第13章:金属伝導の半古典的理論
第14章:フェルミ面の測定
第15章:いくつかの金属のバンド構造
第16章:緩和時間近似を越えた近似
第17章:独立電子近似を越えた近似
第18章:表面効果
付録
金属のバンド構造を具体的に計算するために見つけられたさまざまな方法を説明するのが2冊目である。一般に金属中に含まれている電子どうしの相互作用はシュレディンガー方程式の多体問題だから解析的には計算できないので、この本で紹介されているのはすべて近似計算だ。それらは電子の繰り込み理論や量子電磁気学(QED)以前の半古典的モデルによる近似である。
本書で特に重要なキーワードを解説しているページと短い説明を書いておこう。
バンド構造: http://hooktail.sub.jp/solid/band/
結晶中ではイオン殻による周期的な電場によって、電子のとり得るエネルギーは、いくつかの帯状(バンド状)の領域に限られる。この領域をエネルギーバンドと呼び、電子が取ることの出来ないエネルギー領域をエネルギーギャップと呼ぶ。エネルギーバンド中にどのように電子が入っているかによって、その固体の電気伝導性や光学的特性などが決まる。
独立電子近似:
電子は負の電荷をもっているので互いに避けるように運動する独立電子モデルとはこの「避ける行為」を無視する近似だ。各電子個々のシュレディンガー方程式を考えることで近似する方法である。
自由電子近似:
電子の感じるポテンシャルが非常に弱い場合、電子の振る舞いはほとんど自由な電子とみなすことができる。この自由電子として扱う近似が自由電子近似である。(自由電子モデル、自由電子模型とも言う。)これの対極的な近似が、強結合近似。
セルラー法、マフィンティンポテンシャル、APW法、KKR法、OPW法:
ウィキペディアの「第一原理バンド計算」、「マフィンティンポテンシャル」を参照。
半古典的モデル:
古典力学との対応原理に基づき、古典力学を援用した量子力学の近似理論。準古典論とも呼ばれる。物性物理においては電子波束を古典粒子的に扱うことをいう。
ド・ハース-ファン・アルフェン効果:
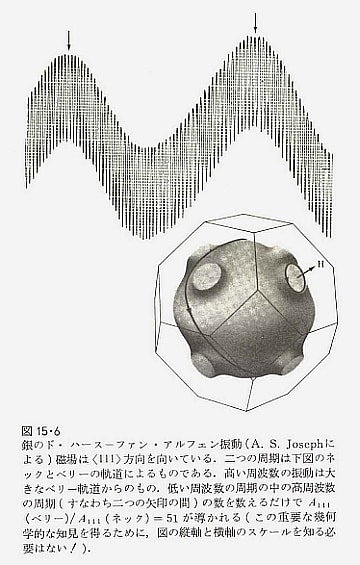
金属の磁化率(帯磁率)が、(十分に低温では)磁場の逆数に比例して振動する現象。この現象は1930年にドハースとファンアルフェンによって実験で発見された。物性物理学の分野においては、重い電子系など、電子の有効質量やフェルミ面の劇的な変化に関連した分野に置いて盛んに用いられる手法の一つとなっている。測定については電気伝導度の比較的高い物質の単結晶が適している。
自由電子のランダウ準位:
磁場の中で荷電粒子がサイクロトロン運動(円運動)するときに取り得る、不連続(離散的)なエネルギーの準位のことである。
磁気音響効果:
超音波が金属に吸収されるとき磁界が存在すると吸収率が大幅に変化する現象をいう。金属の磁界強度に対する超音波吸収においては次の3種類のいずれかが観測される。
(1)サイクロトロン共鳴,(2)幾何学的共鳴吸収,(3) ドハース‐ファンアルフェン効果
ヴィーデマン・フランツの法則:
金属の熱伝導率Kと、電気伝導率σの比が温度に比例することを示したものである。この経験則は、1853年に金属が異なっても温度が同じであればK/σの値がほぼ同じであると報告したグスタフ・ヴィーデマンとルドルフ・フランツから名づけられた。K/σが温度に比例することは1872年にルードヴィヒ・ローレンツが発見した。金属の場合、熱伝導と電気伝導の両方の大部分を自由電子が担うので、この関係が成り立っている。
ハートリー方程式:
多電子系の波動関数を求める代表的な近似法のひとつ。波動関数をスピン軌道の積で近似する。ハートリーの方程式は連立の微積分方程式であるので解くのは簡単ではない。ダグラス・ハートリーは原子の場合に電子間クーロン相互作用を表す項に中心力場近似を用い、かつ自己無撞着場の方法を用いて解を求めることに成功した。ハートリー近似は最も簡単な一電子近似であるが、波動関数が電子座標の入れ替えに対して反対称化されていない。よって電子間の交換相互作用が考慮されていない。またこの点を改良したハートリー・フォック近似と違って、軌道を決めるシュレーディンガー方程式において軌道に作用する演算子が軌道ごとに異なるため、軌道間の直交性が保証されないなどの欠点を持っている。現在ではハートリー近似よりもハートリー・フォック近似のほうが用いられることが多い。
ハートリー・フォック方程式:
多電子系を表すハミルトニアンの固有関数(波動関数)を一個のスレーター行列式で近似(ハートリー=フォック近似)した場合に、それが基底状態に対する最良の近似となるような(スピンを含む)1電子分子軌道の組を探し出すため方程式である。ウラジミール・フォックによって導かれた。分子軌道法の基本となる方程式である。(参考記事:「分子軌道法: 物理学と化学の境界」)
フェルミ液体: https://staff.aist.go.jp/t-yanagisawa/activity/fermi-liquid.html
フェルミ統計に従う量子液体。 1956年 L.D.ランダウが液体ヘリウム3をモデルとしたフェルミ液体の現象論を発表した。ヘリウム3はフェルミ統計に従い,低温ではフェルミ縮退する。一方、液体であるから相互作用は相当強い。金属内の伝導電子系をフェルミ液体として扱うことも可能である。
以下、本書に掲載されている図版を載せておこう。これらの図の原典は1960年代に書かれたれた教科書や論文から本書に引用されたものだ。







この教科書で学んでみようという方は、こちらからどうぞ。
「固体物理の基礎 上・1 固体電子論概論: アシュクロフト、マーミン」- 1981(紹介記事)
「固体物理の基礎 上・2 固体のバンド理論: アシュクロフト、マーミン」- 1981
「固体物理の基礎 下・1 固体フォノンの諸問題: アシュクロフト、マーミン」- 1981
「固体物理の基礎 下・2 固体の物性各論: アシュクロフト、マーミン」- 2008




翻訳のもとになった英語版はこの本だ。1976年刊行。
「Solid State Physics 1e: Neil W. Ashcroft, N.David Mermin」(ハードカバー)(ペーパーバック)

関連ページ: ネットで学びたい方はこちらからどうぞ。
目で見て操作する「分子の世界」-そのミクロ構造と物性-
http://rikanet2.jst.go.jp/contents/cp0200a/start.html
物性物理学(筑波大学物理学系 小野田雅重先生のページ)
http://www.px.tsukuba.ac.jp/~onoda/cmp/cmp.html
結晶回折学 講義資料
http://ceram.material.tohoku.ac.jp/~takamura/class/crystal/crystal.html
ときわ台学:物質・材料の掟 (公開版)
http://www.f-denshi.com/000okite/000matrl.html
関連記事:
固体物理の基礎 上・1 固体電子論概論: アシュクロフト、マーミン
http://blog.goo.ne.jp/ktonegaw/e/af3b66dbda3564a4c49f5d7f722ad777
物性物理30講(物理学30講シリーズ):戸田盛和
http://blog.goo.ne.jp/ktonegaw/e/00d399f545bc69dfa213015f153a312a
基礎の固体物理学: 斯波弘行
http://blog.goo.ne.jp/ktonegaw/e/d2287a9fdbc66eac443fe0888d835602
分子軌道法: 物理学と化学の境界
http://blog.goo.ne.jp/ktonegaw/e/adb9c9e55a1ea2f1883b2a4bfced8f93
応援クリックをお願いします!







「固体物理の基礎 上・2 固体のバンド理論: アシュクロフト、マーミン」

上・2:固体のバンド理論
第11章:バンド構造を計算する他の方法
- 独立電子近似
- 価電子帯波動関数の一般的特徴
- セルラー法
- マフィン-ティン・ポテンシャル
- 補強された平面波(APW)法
- グリーン関数(KKR)法
- 直交化された平面波(OPW)法
- 擬ポテンシャル
第12章:電子の動力学の半古典的モデル
- ブロッホ電子の波束
- 半古典的モデルの一般的特徴
- 静電場
- 正孔の一般論
- 一様な静磁場
- ホール効果と磁気抵抗
第13章:金属伝導の半古典的理論
- 緩和時間近似
- 非平衡分布関数の一般形
- 直流電気伝導度
- 交流電気伝導度
- 熱伝導度
- 熱電気効果
- 磁場中の伝導度
第14章:フェルミ面の測定
- ド・ハース-ファン・アルフェン効果
- 他の振動的な電流磁気効果
- 自由電子のランダウ準位
- ブロッホ電子のランダウ準位
- 振動現象の物理的起源
- 電子スピンの効果
- 磁気音響効果
- 超音波減衰
- 異常表皮効果
- サイクロトロン共鳴
- サイズ効果
第15章:いくつかの金属のバンド構造
- アルカリ金属
- 貴金属
- 2価の単純金属
- 3価の単純金属
- 4価の単純金属
- 半金属
- 遷移金属
- 希土類金属
- 合金
第16章:緩和時間近似を越えた近似
- 電子散乱の原因
- 散乱確率と緩和時間
- 衝突の一般的な記述法
- ボルツマン方程式
- 不純物散乱
- ヴィーデマン・フランツの法則
- マチーセン則
- 等方的な物質における散乱
第17章:独立電子近似を越えた近似
- ハートリー方程式
- ハートリー・フォック方程式
- 相関
- 遮蔽:誘電関数
- トーマス・フェルミとリンドハルトの遮蔽
- ハートリー・フォック近似の遮蔽
- フェルミ液体論
第18章:表面効果
- 仕事関数
- 接触電位
- 熱イオン放射
- 低速電子回折
- 電界イオン顕微鏡
- 表面電子準位
付録
G:シュレディンガー方程式に対する変分原理
H:半古典的運動方程式のハミルトン形式とリュヴィルの定理
I:周期関数に対するグリーンの定理
J:一様な電場または磁場内でバンド遷移の起こらないための条件
K:固体の光学的性質
索引
その他の巻の章立て
上・1:固体電子論概論
第1章:金属のドゥルーデ(Drude)理論
第2章:金属のゾンマーフェルト理論
第3章:自由電子モデルの破綻
第4章:結晶格子
第5章:逆格子
第6章:X線回折による結晶構造の決定
第7章:ブラベー格子の分類と結晶構造の分類
第8章:周期ポテンシャル中の電子状態、一般的性質
第9章:弱い周期ポテンシャルの中の電子
第10章:強く束縛された方法
付録
下・1:固体フォノンの諸問題
第19章:固体の分類
第20章:凝集エネルギー
第21章:静止格子模型の破綻
第22章:調和結晶の古典論
第23章:調和結晶の量子論
第24章:フォノン分散関係の測定
第25章:結晶の非調和効果
第26章:金属中のフォノン
第27章絶縁体の誘電的性質
付録
下・2:半導体、磁性体、超伝導体論
第28章:均質な半導体
第29章:不均質な半導体
第30章:結晶中の欠陥
第31章:反磁性と常磁性
第32章:電子相互作用と磁気的構造
第33章:磁気的秩序
第34章:超伝導
付録