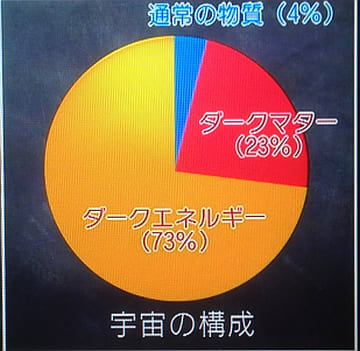
番組ホームページ
先日「番組告知:NHK宇宙白熱教室(ローレンス・クラウス教授)」という記事で告知した4回シリーズ番組の2回目が昨夜放送された。(番組はFC2動画のこのページで見れるようだ。また番組の音声を文字にしたものはこのページで読める。)
今回の講座も「宇宙が始まる前には何があったのか?: ローレンス・クラウス」(紹介記事)には含まれていない内容だ。
「主な内容」、「解説」、「良かった点、素晴らしいと思ったこと」、「改善したほうがよいと思ったこと」、「その他、気がついたこと」というくくりで感想をまとめておこう。
主な内容
このような流れで講義は進んだ。
- 物理学者がどのように物事をとらえているか、その道具を授けたい。
- この世界はとても複雑。単純化して考える。
- 本と紙切れはどちらが先に落ちるか?
- 本のほうが重いから先に落ちるのというのは間違い。
- ガリレオ:「些細なことを気にしなければ、物は同じ速度で落ちる。」
- 紙切れを丸めて落とすと本と同じ時間で落ちる。
- ニュートンの万有引力の法則はガリレオの発見がなかったら導かれなかっただろう。
- 質問1:牧場の生産性を上げるには?エンジニア、心理学者、物理学者の考え
- 物理学者:「牛をだいたい丸だとしましょう。」
- 牛を丸(球)だとして、サイズのスケールが大きいと皮膚が内部圧力に負けて裂けてしまうことを示す。
- 大雑把にとらえれば多くの情報が得られる。
- 宇宙について何を無視し、何を判断すればよいか。答えはやってみなければわからない。
- 太陽を単純な丸ととらえる。太陽のエネルギーによる圧力は重力とつりあっている。
- 猛烈なエネルギーの正体は?石炭の燃焼と考えると1万年で燃え尽きてしまうことがわかる。
- 1920年頃、エディントンは太陽に未知のエネルギーがあると主張。
- ベーテは核融合によって太陽は100億年燃えることを発見。太陽を丸と仮定したことから導かれた。
- 核融合はニュートリノも作り出す。デイビスによるニュートリノの検出。40年後にノーベル賞をとったのも太陽を丸と仮定したおかげ。
- ニュートリノは予測の3分の1しか検出されなかった。
- 単純化によって太陽と地球の間でニュートリノの性質が変化したことが見つかり、素粒子物理学に大きな影響を与えた。
- 「数」を物理学者流にとらえる。10の累乗であらわすと便利。
- 指数法則:掛け算を足し算にして計算することが可能になる。
- すべての数は「k × 10のn乗」という形で書ける。つまり「仮数x10の指数」
- 問題:232x556の概数を3秒で計算せよ。指数が重要。
- フェルミ問題。「物理学者はどんな問題にも答えられなければならない。」
- 問題1:100万まで数えるのに、どのくらいの時間がかかる?
- 問題2:アメリカ全土で1日にどれくらいトイレの水が流されているか?
- 10の指数で考えれば、物事を直観的にとらえ、別の角度から認識できるようになる。
- 問題3:シカゴにはピアノの調律師は何人いるか?
- 問題4:カエサル臨終の一息に含まれていた原子を私たちは一呼吸ごとに何個吸い込んでいるか?
- 次元解析:物理の単位(次元)だけをたよりに「公式」や「未知の量」を推定すること。
- 物理学で表わす量は長さL、時間T、質量Mだけの組み合わせで書き表せる。
- 距離(L)=速さ(L/T)×時間(T)
- 質量Mの錘がつるされたバネの振動周期は?
- バネの振動周期はsqrt(M/k)に比例する。
- 次元が3つあるのは嫌なので1つになってくれればよい。
- 長さと時間を関係付ける普遍的なものがあればよい。それは光速cだ。
- 時間と質量を関係付ける普遍的なものがあればよい。それはプランク定数だ。
- 未知の素粒子の質量が陽子の質量と同じなら、その寿命は陽子の寿命に等しい。
- 陽子の質量は時間に変換することができ、それは10のマイナス24乗秒 (「その他、気がついたこと、生じた疑問」を参照)
- 1974年に陽子の3倍の質量をもつ素粒子が見つかったが寿命は予想の1000倍もあった。
- それは新しい物理法則の存在を意味しノーベル賞につながった。
- それにより強い力の重要な特徴が明らかになった。
- 次元解析は物理を勉強する基礎だけでなく宇宙の秘密を解き明かす手助けになる。
解説
物事を大ざっぱにとらえることで新しい視点から見ることができるようになることを理解するのが今回の講座の目標だ。クラウス博士は「物理学者の考え方」として紹介していたが、この考え方は私生活やビジネスにも応用することができる。
冒頭で「単純化の効用」としてガリレオの実験が講義への導入として紹介された。
次に大ざっぱなスケールで2倍のサイズの「スーパー牛」を考えると、内部圧力によって皮膚が裂けてしまうことが計算で示されたのは面白かった。番組では紹介されなかったが象や恐竜などの皮膚は硬いから内部圧力が強くても裂けないということ、なぜダチョウのタマゴの殻が分厚いかということがわかる。
講義の前半はフェルミ問題を何題か解くことによって大ざっぱな数値で計算練習する。この番組では「フェルミ問題」と訳されていたが、一般的には「フェルミ推定」という言葉で知られている。
フェルミ推定とは特定できない数や調査することが難しい数などを論理的に推論し概算することだ。ネットで検索すると就活系のページが数多くヒットすることからわかるように、概算はビジネスで重要なスキルのひとつである。問題を解くだけでなく、自分で問題を作って解いてみるのも面白いと思う。
フェルミ推定: ウィキペディアの記事
5分で理解するフェルミ推定 マンホールの蓋はいくつある?
http://wakarukoto.com/?p=743
後半は「次元解析」についての話。物理学で扱われる量の単位はすべて「長さ(L)」、「時間(T)」、「質量(M)」の組合せであらわせることを紹介していた。よくわからなかった方は、このページをお読みになるとよいだろう。
次元解析
http://la.b-ed.smz.u-tokai.ac.jp/center/kiso/physics/vectorintro/unit/DIM-ANAL/DIM-ANAL.htm
しかし、これには注意が必要だ。本当にすべての単位をあらわせるのだろうか?たとえばエネルギーはどうだろうか?そして電圧や電流はこれらの単位だけであらわせるのだろうか?番組をご覧になった方の中にはそんなふうに思った人がいたかもしれない。
これはぜひ「赤シャツの少年」に質問してもらいたかった。
エネルギーEは運動エネルギーを E=(1/2)mv^2 とあらわせることから[L],[M], [T]だけで表せることがわかる。アインシュタインの静止エネルギーにしても E=mc^2だから大丈夫。ジュール(J)であらわされる「熱量」もエネルギーの一種だから大丈夫なわけだ。けれども温度は?電圧や電流は?と考えるとよくわからなくなってしまう。音の大きさはデシベルであらわされるけれど、これも3つの単位であらわせるのだろうか?また数学の図形問題で使われる「角度」は3つの単位だけであらわせるのだろうか?
有名な科学者の説明だからといって鵜呑みにしてはいけない。ファインマン先生がおっしゃっていたように自分で疑問を見つけ出すのが大事だし、そのほうがずっと楽しい。
本当のことを言うと物理量をすべてこの3つの単位で表せるというのは正しくない。物理学で「基本単位」と呼んでいるのは7つあるのだ。クラウス博士はこれを知らなかったわけではなく、受講者にとってわかりやすいように「単純化」したのだと思う。
![]()
正確な説明は次のページをお読みいただきたい。
国際単位系(SI)
http://www-lab.ee.uec.ac.jp/text/misc/si_units.html
SI単位系について
http://homepage3.nifty.com/such/shumi/shumi3/si.html
単位と次元
http://www.ele.kochi-tech.ac.jp/tacibana/analog-Web/units-dims.html
このようなSI基本単位系を使って電磁気学で使われる物理量の単位は組み立てられている。長さ、質量、時間だけでなくアンペアの単位も使われていることがおわかりいただけるだろう。表の中の数字は各単位の右上につける累乗の数を意味している。
クリックで拡大
![]()
この表は次のページから拝借させていただいた。
電磁気学の単位系が難しい理由
http://fnorio.com/0096Electromagnetic_unit_system1/Electromagnetic_unit_system1.html
また流体力学や伝熱工学では「無次元数(dimensionless number)」という「単位をもたない量」が使われている。具体的にはレイノルズ数、ビオ数、エッカート数、フーリエ数、グラスホフ数、ヌッセルト数、ペクレ数、プラントル数、レイノルズ数、スタントン数などだ。説明はウィキペディアの「無次元数」をお読みいただきたい。
良かった点、素晴らしいと思ったこと
- 大ざっぱにとらえること、次元解析を使った考え方をすることによってノーベル賞に結びつくような大発見がなされたというのは、ものすごく説得力があり、素晴らしいと思った。
改善したほうがよいと思ったこと
- 次元解析の例をもう少し詳しく、他の例も取り上げる形で説明したほうがよかったと思う。理由は上の「解説」で述べたとおりだ。
一般視聴者には分かりにくかったこと
- 次元解析の説明のところで振り子の振動周期の説明でルート(平方根)を使った式が例示されたが、理解できなかった人は多かったと思う。これは仕方がないことだ。
- 大ざっぱにとらえたり、次元解析を使った考え方をすることでノーベル賞級の発見に結びついたことが紹介されたが、どうしてそうなったかということが論理的な筋道を追った形で理解できなかった。けれどもそれは仕方がない。なぜならそれを理解するためには、ノーベル賞受賞の理由となった物理学の業績、研究テーマを理解しなければならないからだ。
- 次元解析の説明の最後で単位の数を減らす方法が解説されていた。プランク定数がでてきたが、このあたりは量子力学を学ばないと理解できないことだ。
その他、気がついたこと、生じた疑問
- 大ざっぱにとらえることが大切なのは十分理解しているが、第3回、第4回の話にどうつながるのかが僕には想像できていない。というのもこの20年間の宇宙論の発展は「精密な観測」を行うことで実現された成果であるからだ。「大ざっぱ」と「精密」は正反対である。次回の放送で今回の話がどうつながるのか確認してみたい。
- 陽子の寿命が間違っていた。この件についてはT_NAKAさんからご指摘いただいたのだが、いただいたコメントと僕の返信をそのままここに書いておく。そしてその後 hirotaさんからもコメントをいただいたので本文に記載させていただきました。
T_NAKAさんのコメント:
タイトル:陽子崩壊
陽子崩壊を観測するためにカミオカンデを作ったわけですが、今のところ観測されていないので陽子の寿命は 10^33年 以上ということだと思っています。しかし、この講義だと陽子の寿命が 10^(-24)sec のように表現されたと感じました。私の勘違いなのかも知れませんので、2ケ国語放送だったので原語で聴かれた方はどの様に理解されたのでしょうか?
T_NAKAさんへの僕の返信:
日本語と英語の両方で聞きなおしてみました。翻訳は正確で日本語は英語と同じ内容を伝えています。
博士のしゃべった内容(台詞)はこのアドレスですべて読めます。
http://o.x0.com/m/48836
クラウス博士は陽子の寿命のことを勘違いしていますね。陽子の寿命はT_NAKAさんがおっしゃるようにとても長く10^33年以上で、けして10^(-24)秒ではありません。
問題の箇所は番組の最後の「次元解析」の話の締めの部分です。プランク定数の紹介の直後です。
「新粒子が陽子と同じ程度の質量ならば(陽子と同じく)寿命は10^(-24)秒と予想される。」という発言。
この新粒子はJ/Ψ中間子であることがすぐ次に続きます。
ウィキペディアの「粒子崩壊」という記事の「素粒子の寿命」の表を見ると、J/Ψ中間子の質量と寿命は3096.9 MeV、10^-20秒となっています。
また陽子の質量は938.272046(21) MeVと書かれています。
陽子と他の素粒子を勘違いしたのかなと、他の素粒子の寿命を調べたところ10^(-24)秒に近いのはWボソンやZ粒子しかなくて、寿命はどちらも10^-25乗秒です。
でもこの二つの粒子は「弱い力」に関係する粒子で、ここで博士が言及した「強い力」とは関係なさそうです。結局、どうすれば正しい説明になるのかはわかりませんが、ともかくこのあたりは間違ったことを言っているようですね。
hirotaさんからいただいたコメント:
タイトル:質量-時間
質量を時間に変換するというのは寿命じゃないです。
「普遍定数に光速があるから時間と空間が同等,エネルギーと質量が同等」と同じ意味で、プランク定数でエネルギーが時間に換算できるという意味です。
プランク定数:h=6.6*10^(-34) m^2kg/s, 陽子質量:m=1.7*10^(-27) kg, 光速:c=3*10^8 m/s
より h/(mc^2)=4*10^(-24) s
hirotaさんへの僕の返信:
なるほど、理解できましたプランク定数でエネルギーが時間に換算できるという意味にすぎず、その時間とは「寿命」ではなかったわけですね。教えていただきありがとうございます。番組では次のように表現されていましたから、クラウス教授はそれを寿命だと勘違いしていることになります。
「陽子の質量は時間に変換すると「10のマイナス24乗秒」だ。だからもし陽子と同じ程度の質量を持つ新粒子が発見されそれが不安定で寿命を持つなら私はそれを大体10のマイナス24乗秒だと予測するだろう。それは実際正しい予測だった。だが1974年に陽子の3倍の質量を持つ新しい素粒子が見つかりその寿命が「10のマイナス21乗秒」だと分かった。」
T_NAKAさんからいただいたコメント:
「だからもし陽子と同じ程度の質量を持つ新粒子が発見されそれが不安定で寿命を持つなら私はそれを大体10のマイナス24乗秒だと予測するだろう」というセリフを読むと、「それが不安定で寿命を持つなら」という条件で、不確定性原理から「大体10のマイナス24乗秒」ということなんじゃないかと理解しました。陽子のように安定した粒子の寿命を算定するのに不確定性原理を使うのは不適切ですが、同程度の質量の「不安定な粒子」にはこの計算で概算できるということなんでしょう。
hirotaさんからいただいたコメント:
一応、不確定性関係 ΔEΔt 〜 h による仮想粒子の寿命ではありますね。
番組関連書籍:
「宇宙が始まる前には何があったのか?:ローレンス・クラウス」(紹介記事)
「A Universe from Nothing: Lawrence M. Krauss」(Kindle版)
![]()
![]()
クラウス教授の著書をAmazonで検索する: 単行本(日本語) 単行本(英語) Kindle版(英語)
応援クリックをお願いします!
![にほんブログ村 科学ブログ 物理学へ]()
![人気ブログランキングへ]()
![]()
![]()
参考書籍:
「インフレーション宇宙論―ビッグバンの前に何が起こったのか:佐藤勝彦」
「宇宙,無からの創生―138億年の仮説はほんとうか(Newton別冊)」
![]()
![]()
関連記事:
番組告知:NHK宇宙白熱教室(ローレンス・クラウス教授)
http://blog.goo.ne.jp/ktonegaw/e/fdcf3a5173e9f55fc37c9b8d85f4128b
宇宙が始まる前には何があったのか?: ローレンス・クラウス
http://blog.goo.ne.jp/ktonegaw/e/b6f36e8eedba5ee63a4f919d30a2cb20
感想:NHK宇宙白熱教室:第1回:宇宙のスケールを体感する! 〜空間・時間・物質〜
http://blog.goo.ne.jp/ktonegaw/e/88f1e3ca688959fc0ace6e0999085521
番組告知:MIT白熱教室(物理学編)、これが物理学だ!
http://blog.goo.ne.jp/ktonegaw/e/66d25e29fc2c514f453a6b110150b811
番組告知:バークレー白熱教室〜大統領を目指す君のためのサイエンス
http://blog.goo.ne.jp/ktonegaw/e/36bb14b19b9ca57d17fe60655a704615
ファインマンさんの流儀:ローレンス M.クラウス著、吉田三知世訳
http://blog.goo.ne.jp/ktonegaw/e/9ec9faa4bd78881bd1986bf7773cc390
超ひも理論を疑う:ローレンス M.クラウス
http://blog.goo.ne.jp/ktonegaw/e/d5aefd0f455c43b62365954cd2ae601c
先日「番組告知:NHK宇宙白熱教室(ローレンス・クラウス教授)」という記事で告知した4回シリーズ番組の2回目が昨夜放送された。(番組はFC2動画のこのページで見れるようだ。また番組の音声を文字にしたものはこのページで読める。)
今回の講座も「宇宙が始まる前には何があったのか?: ローレンス・クラウス」(紹介記事)には含まれていない内容だ。
「主な内容」、「解説」、「良かった点、素晴らしいと思ったこと」、「改善したほうがよいと思ったこと」、「その他、気がついたこと」というくくりで感想をまとめておこう。
主な内容
このような流れで講義は進んだ。
- 物理学者がどのように物事をとらえているか、その道具を授けたい。
- この世界はとても複雑。単純化して考える。
- 本と紙切れはどちらが先に落ちるか?
- 本のほうが重いから先に落ちるのというのは間違い。
- ガリレオ:「些細なことを気にしなければ、物は同じ速度で落ちる。」
- 紙切れを丸めて落とすと本と同じ時間で落ちる。
- ニュートンの万有引力の法則はガリレオの発見がなかったら導かれなかっただろう。
- 質問1:牧場の生産性を上げるには?エンジニア、心理学者、物理学者の考え
- 物理学者:「牛をだいたい丸だとしましょう。」
- 牛を丸(球)だとして、サイズのスケールが大きいと皮膚が内部圧力に負けて裂けてしまうことを示す。
- 大雑把にとらえれば多くの情報が得られる。
- 宇宙について何を無視し、何を判断すればよいか。答えはやってみなければわからない。
- 太陽を単純な丸ととらえる。太陽のエネルギーによる圧力は重力とつりあっている。
- 猛烈なエネルギーの正体は?石炭の燃焼と考えると1万年で燃え尽きてしまうことがわかる。
- 1920年頃、エディントンは太陽に未知のエネルギーがあると主張。
- ベーテは核融合によって太陽は100億年燃えることを発見。太陽を丸と仮定したことから導かれた。
- 核融合はニュートリノも作り出す。デイビスによるニュートリノの検出。40年後にノーベル賞をとったのも太陽を丸と仮定したおかげ。
- ニュートリノは予測の3分の1しか検出されなかった。
- 単純化によって太陽と地球の間でニュートリノの性質が変化したことが見つかり、素粒子物理学に大きな影響を与えた。
- 「数」を物理学者流にとらえる。10の累乗であらわすと便利。
- 指数法則:掛け算を足し算にして計算することが可能になる。
- すべての数は「k × 10のn乗」という形で書ける。つまり「仮数x10の指数」
- 問題:232x556の概数を3秒で計算せよ。指数が重要。
- フェルミ問題。「物理学者はどんな問題にも答えられなければならない。」
- 問題1:100万まで数えるのに、どのくらいの時間がかかる?
- 問題2:アメリカ全土で1日にどれくらいトイレの水が流されているか?
- 10の指数で考えれば、物事を直観的にとらえ、別の角度から認識できるようになる。
- 問題3:シカゴにはピアノの調律師は何人いるか?
- 問題4:カエサル臨終の一息に含まれていた原子を私たちは一呼吸ごとに何個吸い込んでいるか?
- 次元解析:物理の単位(次元)だけをたよりに「公式」や「未知の量」を推定すること。
- 物理学で表わす量は長さL、時間T、質量Mだけの組み合わせで書き表せる。
- 距離(L)=速さ(L/T)×時間(T)
- 質量Mの錘がつるされたバネの振動周期は?
- バネの振動周期はsqrt(M/k)に比例する。
- 次元が3つあるのは嫌なので1つになってくれればよい。
- 長さと時間を関係付ける普遍的なものがあればよい。それは光速cだ。
- 時間と質量を関係付ける普遍的なものがあればよい。それはプランク定数だ。
- 未知の素粒子の質量が陽子の質量と同じなら、その寿命は陽子の寿命に等しい。
- 陽子の質量は時間に変換することができ、それは10のマイナス24乗秒 (「その他、気がついたこと、生じた疑問」を参照)
- 1974年に陽子の3倍の質量をもつ素粒子が見つかったが寿命は予想の1000倍もあった。
- それは新しい物理法則の存在を意味しノーベル賞につながった。
- それにより強い力の重要な特徴が明らかになった。
- 次元解析は物理を勉強する基礎だけでなく宇宙の秘密を解き明かす手助けになる。
解説
物事を大ざっぱにとらえることで新しい視点から見ることができるようになることを理解するのが今回の講座の目標だ。クラウス博士は「物理学者の考え方」として紹介していたが、この考え方は私生活やビジネスにも応用することができる。
冒頭で「単純化の効用」としてガリレオの実験が講義への導入として紹介された。
次に大ざっぱなスケールで2倍のサイズの「スーパー牛」を考えると、内部圧力によって皮膚が裂けてしまうことが計算で示されたのは面白かった。番組では紹介されなかったが象や恐竜などの皮膚は硬いから内部圧力が強くても裂けないということ、なぜダチョウのタマゴの殻が分厚いかということがわかる。
講義の前半はフェルミ問題を何題か解くことによって大ざっぱな数値で計算練習する。この番組では「フェルミ問題」と訳されていたが、一般的には「フェルミ推定」という言葉で知られている。
フェルミ推定とは特定できない数や調査することが難しい数などを論理的に推論し概算することだ。ネットで検索すると就活系のページが数多くヒットすることからわかるように、概算はビジネスで重要なスキルのひとつである。問題を解くだけでなく、自分で問題を作って解いてみるのも面白いと思う。
フェルミ推定: ウィキペディアの記事
5分で理解するフェルミ推定 マンホールの蓋はいくつある?
http://wakarukoto.com/?p=743
後半は「次元解析」についての話。物理学で扱われる量の単位はすべて「長さ(L)」、「時間(T)」、「質量(M)」の組合せであらわせることを紹介していた。よくわからなかった方は、このページをお読みになるとよいだろう。
次元解析
http://la.b-ed.smz.u-tokai.ac.jp/center/kiso/physics/vectorintro/unit/DIM-ANAL/DIM-ANAL.htm
しかし、これには注意が必要だ。本当にすべての単位をあらわせるのだろうか?たとえばエネルギーはどうだろうか?そして電圧や電流はこれらの単位だけであらわせるのだろうか?番組をご覧になった方の中にはそんなふうに思った人がいたかもしれない。
これはぜひ「赤シャツの少年」に質問してもらいたかった。
エネルギーEは運動エネルギーを E=(1/2)mv^2 とあらわせることから[L],[M], [T]だけで表せることがわかる。アインシュタインの静止エネルギーにしても E=mc^2だから大丈夫。ジュール(J)であらわされる「熱量」もエネルギーの一種だから大丈夫なわけだ。けれども温度は?電圧や電流は?と考えるとよくわからなくなってしまう。音の大きさはデシベルであらわされるけれど、これも3つの単位であらわせるのだろうか?また数学の図形問題で使われる「角度」は3つの単位だけであらわせるのだろうか?
有名な科学者の説明だからといって鵜呑みにしてはいけない。ファインマン先生がおっしゃっていたように自分で疑問を見つけ出すのが大事だし、そのほうがずっと楽しい。
本当のことを言うと物理量をすべてこの3つの単位で表せるというのは正しくない。物理学で「基本単位」と呼んでいるのは7つあるのだ。クラウス博士はこれを知らなかったわけではなく、受講者にとってわかりやすいように「単純化」したのだと思う。

正確な説明は次のページをお読みいただきたい。
国際単位系(SI)
http://www-lab.ee.uec.ac.jp/text/misc/si_units.html
SI単位系について
http://homepage3.nifty.com/such/shumi/shumi3/si.html
単位と次元
http://www.ele.kochi-tech.ac.jp/tacibana/analog-Web/units-dims.html
このようなSI基本単位系を使って電磁気学で使われる物理量の単位は組み立てられている。長さ、質量、時間だけでなくアンペアの単位も使われていることがおわかりいただけるだろう。表の中の数字は各単位の右上につける累乗の数を意味している。
クリックで拡大

この表は次のページから拝借させていただいた。
電磁気学の単位系が難しい理由
http://fnorio.com/0096Electromagnetic_unit_system1/Electromagnetic_unit_system1.html
また流体力学や伝熱工学では「無次元数(dimensionless number)」という「単位をもたない量」が使われている。具体的にはレイノルズ数、ビオ数、エッカート数、フーリエ数、グラスホフ数、ヌッセルト数、ペクレ数、プラントル数、レイノルズ数、スタントン数などだ。説明はウィキペディアの「無次元数」をお読みいただきたい。
良かった点、素晴らしいと思ったこと
- 大ざっぱにとらえること、次元解析を使った考え方をすることによってノーベル賞に結びつくような大発見がなされたというのは、ものすごく説得力があり、素晴らしいと思った。
改善したほうがよいと思ったこと
- 次元解析の例をもう少し詳しく、他の例も取り上げる形で説明したほうがよかったと思う。理由は上の「解説」で述べたとおりだ。
一般視聴者には分かりにくかったこと
- 次元解析の説明のところで振り子の振動周期の説明でルート(平方根)を使った式が例示されたが、理解できなかった人は多かったと思う。これは仕方がないことだ。
- 大ざっぱにとらえたり、次元解析を使った考え方をすることでノーベル賞級の発見に結びついたことが紹介されたが、どうしてそうなったかということが論理的な筋道を追った形で理解できなかった。けれどもそれは仕方がない。なぜならそれを理解するためには、ノーベル賞受賞の理由となった物理学の業績、研究テーマを理解しなければならないからだ。
- 次元解析の説明の最後で単位の数を減らす方法が解説されていた。プランク定数がでてきたが、このあたりは量子力学を学ばないと理解できないことだ。
その他、気がついたこと、生じた疑問
- 大ざっぱにとらえることが大切なのは十分理解しているが、第3回、第4回の話にどうつながるのかが僕には想像できていない。というのもこの20年間の宇宙論の発展は「精密な観測」を行うことで実現された成果であるからだ。「大ざっぱ」と「精密」は正反対である。次回の放送で今回の話がどうつながるのか確認してみたい。
- 陽子の寿命が間違っていた。この件についてはT_NAKAさんからご指摘いただいたのだが、いただいたコメントと僕の返信をそのままここに書いておく。そしてその後 hirotaさんからもコメントをいただいたので本文に記載させていただきました。
T_NAKAさんのコメント:
タイトル:陽子崩壊
陽子崩壊を観測するためにカミオカンデを作ったわけですが、今のところ観測されていないので陽子の寿命は 10^33年 以上ということだと思っています。しかし、この講義だと陽子の寿命が 10^(-24)sec のように表現されたと感じました。私の勘違いなのかも知れませんので、2ケ国語放送だったので原語で聴かれた方はどの様に理解されたのでしょうか?
T_NAKAさんへの僕の返信:
日本語と英語の両方で聞きなおしてみました。翻訳は正確で日本語は英語と同じ内容を伝えています。
博士のしゃべった内容(台詞)はこのアドレスですべて読めます。
http://o.x0.com/m/48836
クラウス博士は陽子の寿命のことを勘違いしていますね。陽子の寿命はT_NAKAさんがおっしゃるようにとても長く10^33年以上で、けして10^(-24)秒ではありません。
問題の箇所は番組の最後の「次元解析」の話の締めの部分です。プランク定数の紹介の直後です。
「新粒子が陽子と同じ程度の質量ならば(陽子と同じく)寿命は10^(-24)秒と予想される。」という発言。
この新粒子はJ/Ψ中間子であることがすぐ次に続きます。
ウィキペディアの「粒子崩壊」という記事の「素粒子の寿命」の表を見ると、J/Ψ中間子の質量と寿命は3096.9 MeV、10^-20秒となっています。
また陽子の質量は938.272046(21) MeVと書かれています。
陽子と他の素粒子を勘違いしたのかなと、他の素粒子の寿命を調べたところ10^(-24)秒に近いのはWボソンやZ粒子しかなくて、寿命はどちらも10^-25乗秒です。
でもこの二つの粒子は「弱い力」に関係する粒子で、ここで博士が言及した「強い力」とは関係なさそうです。結局、どうすれば正しい説明になるのかはわかりませんが、ともかくこのあたりは間違ったことを言っているようですね。
hirotaさんからいただいたコメント:
タイトル:質量-時間
質量を時間に変換するというのは寿命じゃないです。
「普遍定数に光速があるから時間と空間が同等,エネルギーと質量が同等」と同じ意味で、プランク定数でエネルギーが時間に換算できるという意味です。
プランク定数:h=6.6*10^(-34) m^2kg/s, 陽子質量:m=1.7*10^(-27) kg, 光速:c=3*10^8 m/s
より h/(mc^2)=4*10^(-24) s
hirotaさんへの僕の返信:
なるほど、理解できましたプランク定数でエネルギーが時間に換算できるという意味にすぎず、その時間とは「寿命」ではなかったわけですね。教えていただきありがとうございます。番組では次のように表現されていましたから、クラウス教授はそれを寿命だと勘違いしていることになります。
「陽子の質量は時間に変換すると「10のマイナス24乗秒」だ。だからもし陽子と同じ程度の質量を持つ新粒子が発見されそれが不安定で寿命を持つなら私はそれを大体10のマイナス24乗秒だと予測するだろう。それは実際正しい予測だった。だが1974年に陽子の3倍の質量を持つ新しい素粒子が見つかりその寿命が「10のマイナス21乗秒」だと分かった。」
T_NAKAさんからいただいたコメント:
「だからもし陽子と同じ程度の質量を持つ新粒子が発見されそれが不安定で寿命を持つなら私はそれを大体10のマイナス24乗秒だと予測するだろう」というセリフを読むと、「それが不安定で寿命を持つなら」という条件で、不確定性原理から「大体10のマイナス24乗秒」ということなんじゃないかと理解しました。陽子のように安定した粒子の寿命を算定するのに不確定性原理を使うのは不適切ですが、同程度の質量の「不安定な粒子」にはこの計算で概算できるということなんでしょう。
hirotaさんからいただいたコメント:
一応、不確定性関係 ΔEΔt 〜 h による仮想粒子の寿命ではありますね。
番組関連書籍:
「宇宙が始まる前には何があったのか?:ローレンス・クラウス」(紹介記事)
「A Universe from Nothing: Lawrence M. Krauss」(Kindle版)


クラウス教授の著書をAmazonで検索する: 単行本(日本語) 単行本(英語) Kindle版(英語)
応援クリックをお願いします!




参考書籍:
「インフレーション宇宙論―ビッグバンの前に何が起こったのか:佐藤勝彦」
「宇宙,無からの創生―138億年の仮説はほんとうか(Newton別冊)」


関連記事:
番組告知:NHK宇宙白熱教室(ローレンス・クラウス教授)
http://blog.goo.ne.jp/ktonegaw/e/fdcf3a5173e9f55fc37c9b8d85f4128b
宇宙が始まる前には何があったのか?: ローレンス・クラウス
http://blog.goo.ne.jp/ktonegaw/e/b6f36e8eedba5ee63a4f919d30a2cb20
感想:NHK宇宙白熱教室:第1回:宇宙のスケールを体感する! 〜空間・時間・物質〜
http://blog.goo.ne.jp/ktonegaw/e/88f1e3ca688959fc0ace6e0999085521
番組告知:MIT白熱教室(物理学編)、これが物理学だ!
http://blog.goo.ne.jp/ktonegaw/e/66d25e29fc2c514f453a6b110150b811
番組告知:バークレー白熱教室〜大統領を目指す君のためのサイエンス
http://blog.goo.ne.jp/ktonegaw/e/36bb14b19b9ca57d17fe60655a704615
ファインマンさんの流儀:ローレンス M.クラウス著、吉田三知世訳
http://blog.goo.ne.jp/ktonegaw/e/9ec9faa4bd78881bd1986bf7773cc390
超ひも理論を疑う:ローレンス M.クラウス
http://blog.goo.ne.jp/ktonegaw/e/d5aefd0f455c43b62365954cd2ae601c