「
宇宙が始まる前には何があったのか?:ローレンス・クラウス」
内容紹介
ビッグバンの前には何があったのか?その最大の謎を、現代の量子物理学は解きあかしつつある。物質と反物質のわずかな非対称から生じたゆらぎ、それが今日の私たちの宇宙を形作った。それは無から有が生まれることであり、無からエネルギーが生じるという物理学の直感と常識に反したことだった。全米でベストセラー、アリゾナ州立大学の宇宙物理学者による衝撃の書。
著者略歴
ローレンス・クラウス
宇宙物理学者。アリゾナ州立大学にて「起源プロジェクト」を創設し率いる。1995年、「真空のエネルギーは、非常に小さいがゼロではない」という大胆な説をマイケル・ターナーとともに提唱。当時は異端視されたが後に見事、実証される。2012年には全米科学審議会から「公益賞」を授与された。
翻訳者略歴
青木薫
1956年、山形県生まれ。京都大学理学部卒、同大学院修了。理学博士。翻訳家。2007年の日本数学会出版賞を受賞している
理数系書籍のレビュー記事は本書で254冊目。
2014年6月20日から放送されるNHK Eテレ『
宇宙白熱教室』(毎週金曜23時〜 全4回)のテキストとも言うべき一冊。
「種の起源」に匹敵! 宇宙論のパラダイムシフト
無からなぜ有が生まれたのか? 最先端の量子物理学は宇宙誕生の謎を解明しつつある。
宇宙は平坦だった、加速膨張する宇宙、2兆年後はすべての天体が姿を消す……。
「種の起源」にも匹敵すると賞賛された全米ベストセラーとなった本書は、コンパクトなサイズなのに、脳みそを鷲づかみにされるような濃密さに満ち満ちています。
科学翻訳の第一人者・青木薫氏による奥深く精密な文章と大胆な解説もお見逃しなく。
今夜からの放送開始に間に合わせるため、急きょ本書を読んでみた。
中学時代の教頭先生が天文ファンだったことがきっかけで、僕は中学1年の頃から毎月「
月刊天文ガイド」を買うような少年だった。自作の屈折望遠鏡で観測した月面のスケッチを教頭先生に見せるために、週に一度は職員室へ行っていた。今よりだいぶのどかで平和な1970年代後半のことだ。
中学2年だった1976年7月と9月にはNASAが打ち上げた
バイキング1号と
2号が相次いで火星表面に着陸し、鮮明なカラー写真を地球に送ってきていた。今から40年近く前のことだが、惑星科学はそこまで進歩していたのだ。
人類が初めて目にした火星表面のカラー写真
(写真クリックでこの翌日に撮られた写真を表示?)
![]()
宇宙の広がりを意識しだしたのもその頃だ。今では売られていない「
全天恒星図」をたよりに星雲や星団に見入ったりして、宇宙はいったいどこまで広がっているのだろう?宇宙の果てというのはあるのだろうか?などと想像していた。
当時はまだ
ハッブル宇宙望遠鏡(1990年に打ち上げ)や
すばる望遠鏡(1999年観測開始)もなく、今よりずっと不鮮明な天体写真集しか手に入らない。だとしても天体観望会の双眼鏡で見るより、はるかに鮮明に大写しされたはるか彼方の銀河や星団の写真に心をときめかせていたものだ。
宇宙がビッグバンから始まったのは知っていた。ブルーバックスの相対性理論についての本を読んでいたので、宇宙空間は曲率によって「開いている」か「閉じている」か「平坦」かのどれかひとつであるということも知っていた。ただ、観測可能な宇宙の果てが何億光年離れているのかについては、知っていたのかどうか覚えていない。130億光年というのは当時から知られていた距離なのだろうか?
僕の「天文熱」は大学に入学するころまで続き、その後ほかのことに関心が移ってしまったので自然に消えていった。だから僕の天文学や宇宙の知識は1970年代から80年代初めで止まったままなのだ。持っている天文学の本も「
とねの本棚(天文学)」をご覧いただければわかるように、当時のものが半分を占めている。
高校1年のときに6000円で購入した「
現代天文学 第2版(1978年):A.ウンゼルト著、小平桂一訳」を見てみると、宇宙の年齢(観測可能な宇宙の果てまでの距離)は130億年で誤差は±5億年と書いてあった。この本で僕が宇宙論について得ていた知識を書き出すと次のようになる。
- ハッブルの法則により宇宙が膨張していることは知られていた。
- 宇宙の年齢(宇宙の端までの距離)=130億年で誤差は±5億年
- 世界最大の望遠鏡(パロマー山の5m望遠鏡)で光学的に確認できる宇宙は20億光年まで。
- 宇宙背景輻射は1965年以降、ノイズとして観測され、その温度は絶対温度で2.7度だとわかっていた。
- 曲率が正、負、ゼロの宇宙の3つの可能性があることが予想されていた。
- 宇宙がビッグバンで始まり、宇宙の晴れ上がりがあったことは予想されていた。
- ビッグバンの詳細は全くわかっていなかった。特異点で始まるという矛盾をかかえていた。
当時のビッグバンのイメージ(宇宙は点から始まる。)
![]()
曲率が正、負、ゼロの宇宙の2次元的なイメージ
![]()
今の高校生はどんなふうに宇宙のことを学んでいるのだろうか?
「
NHK高校講座 地学基礎」のページで
動画を確認したところ、僕が学んでいたころの内容とほとんど違いがないことがわかった。
たとえば70億年前に始まった加速的膨張の図示や解説はされていない。
![]()
インフレーションらしきものは先っぽに図示されているがその解説はなく、単にビッグバンとしてだけ紹介されているだけだ。宇宙の誕生も約140億年前と大ざっぱだ。
![]()
ただし「地学基礎」はすべての高校生が学んでいるわけではない。「科学と人間生活」,「物理基礎」,「化学基礎」,「生物基礎」,「地学基礎」のうち「科学と人間生活」を含む2科目,又は,「物理基礎」,「化学基礎」,「生物基礎」,「地学基礎」のうちから3科目を選択するように決められているからだ。「地学基礎」を選択している高校生は少数派だと思われる。
その後、1981年に
科学雑誌Newtonが創刊され、天文関連の記事を僕はときどき見かけていた。そして1995年あたりから次のようなことが取り上げられるようになってきたのだ。
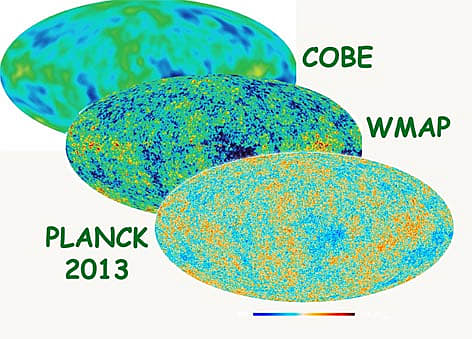
- 宇宙背景放射の精密な観測(COBE、WMAP、Plank 2013)
- インフレーション宇宙論
- 宇宙は「無」から始まった
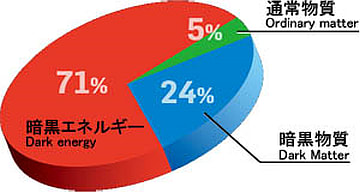
- ダークマター(暗黒物質)、ダークエネルギー(暗黒エネルギー)とその比率
- 130億光年彼方の宇宙の写真
- 宇宙の年齢は137億2千万年
- 70億年前から始まった宇宙の加速的膨張
- 重力波の観測装置の建設、重力レンズ効果の精密な観測
- 人間原理、ランドスケープ問題
- マルチバース(多宇宙)
言葉とイメージを断片的に知っていたという程度で、それらにどういう意味があるのか僕にはよくわかっていなかった。中学生のころより「もう少し詳しく宇宙のことが解明されてきたのだろう」とういう程度の認識のまま現在に至っていたのだ。むしろ、探査機を実際に向かわせる惑星探査の進歩のほうがめざましいと思っていた。
でもそれが大間違いなのはもちろんで、「
重力とは何か:大栗博司」の第4章「ブラックホールと宇宙のはじまり - アインシュタイン理論の限界」を読んだとき気がつかされた。この章には本書「
宇宙が始まる前には何があったのか?:ローレンス・クラウス」で解説されていることのあらましが紹介されていたからだ。
つまり、わずか20年の間に宇宙論は劇的に進歩していたことになる。上記のキーワードであらわされる事柄が、いつ頃どのように解明されていったか筋道をたてて理解するためには本書を読むのがいちばんなのだ。これまでにもクラウス教授の本や青木薫さんの翻訳書は僕は何冊か読んでいる。その中でも宇宙論の入門書として特にお勧めしたい本なのだ。
章立ては次のとおり。
目次
まえがき 宇宙は無から生じた
はじめに 何もないところから、何かが生まれなくてはならない
第1章 いかに始まったのか?
第2章 いかに終わるのか?
第3章 時間の始まりからやってきた光
第4章 ディラックの方程式
第5章 99パーセントの宇宙は見えない
第6章 光速を超えて膨張する
第7章 2兆年後には銀河系以外は見えなくなる
第8章 その偶然は人間が存在するから?
第9章 量子のゆらぎ
第10章 物質と反物質の非対称
第11章 無限の未来には
あとがき リチャード・ドーキンス
訳者解説 青木薫
個々の事柄の論理関係を理解するのが大切だが、この20年で明らかになったことをかいつまんで説明すると次のようになる。
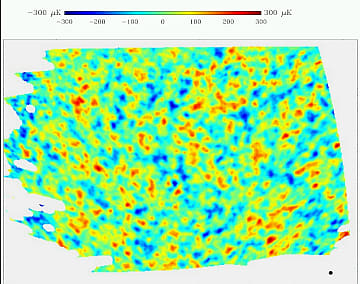
- 生まれて間もない高温の宇宙で発せられた光の残照、それが宇宙マイクロ波背景放射である。宇宙誕生の瞬間を見ることは不可能だ。しかし誕生から30万年後の姿は見ることができる。宇宙背景放射の精密な観測(COBE、WMAP、Plank 2013)が行われ、宇宙誕生時のプランクスケール(超ミクロなスケール)での量子力学的な不確定性原理による揺らぎが全方向について確認された。これは宇宙誕生時にインフレーション(劇的な膨張)がマクロな世界でも見れるほど揺らぎを拡大させたことを意味している。
![]()
COBE(1989年に打ち上げ):
ウィキペディアの記事
WMAP(2001年に打ち上げ):
ウィキペディアの記事
Plank 2013(2009年に打ち上げ):
ウィキペディアの記事
- 宇宙誕生時のビッグバンとインフレーション、宇宙の晴れ上がりから現在までは次のような図で説明される。
![]()
- 130億光年離れた宇宙を撮影できるようになった。これは2006年12月に公開された写真。赤外線宇宙望遠鏡「スピッツァー」の観測画像を解析し、宇宙誕生後10億年以内の光だけを残すことに成功した。宇宙誕生後10億年以内の光だけを残した映像が左側の写真。
![]()
- 宇宙は「無」から誕生した。「無」から物質が生成するしくみは量子力学の「粒子の対生成・対消滅」、量子電磁力学の「仮想粒子」の理論が根拠とされる。その直後にインフレーションがおきた。また、宇宙背景放射は揺らいでいるものの、その揺らぎの量は小さく全体的には均一である。その均一性はその小さな「無」の領域が真空エネルギーで満たされていて相転移をすることで、指数的な膨張がおきたことを示している。宇宙背景放射のわずかな揺らぎとは「無」から生まれた物質と反物質のわずかな非対称から生じたのだ。
粒子の対生成・対消滅
![]()
仮想粒子
![]()
この「無」には2つの選択肢が候補として考えられている。1つはプランクスケール程度のサイズのあらかじめ存在している空間の中で何かが生じる場合。もうひとつは空間が存在しないところから空間が生じる場合である。これらの「無」は宗教や神学者が説くところの「無」とは全く異なるものだ。後者の「無」については本書では「まだよくわかっていない。」という立場をとっているが、現代の数学者や数理物理学者が考えている仮説は次の記事でお読みいただける。
時間とは何か、空間とは何か: S.マジッド、A.コンヌ、R.ペンローズ他
http://blog.goo.ne.jp/ktonegaw/e/d80d021f4fba492bf0e3f47615289422
- 通常の物質とダークマター(暗黒物質)、ダークエネルギー(暗黒エネルギー)の比率はこのように予想されている。ただし本書では通常の物質は1パーセントだと紹介されている。
![]()
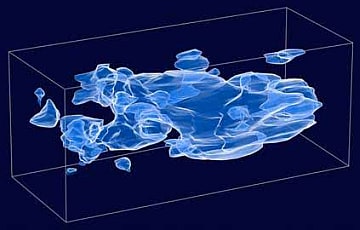
- ダークマター(暗黒物質)の存在やその量は重力レンズ効果の測定による銀河団の質量分布の解析や銀河の回転速度の精密な測定によって予想されている。ダークマターが何でできているかはまだ解明されていない。もっと詳しく言えば、ダークマターの存在を示唆する根拠は銀河の回転速度、弾丸銀河団のような銀河団による背景物体の重力レンズ効果、そして銀河および銀河団を取り巻く熱い気体の温度分布などの観測結果である。
![]()
ダークマターの概念図
![]()
- ダークエネルギー(暗黒エネルギー)は70億年前から始まった宇宙の加速的膨張によって予想されるようになった。それが何なのかはまだ解明されていない。加速的膨張はダークエネルギーの斥力的な重力による。70億年前から始まった宇宙の加速的膨張は標準光度の超新星爆発を使った距離測定(ハッブル定数の測定)によって明らかになった。1998年のこと。
![]()
- 宇宙の曲率がゼロ、すなわち宇宙空間が大域的には平坦(曲率がゼロ)であることは1997年に南極大陸で行われた
BOOMERanG実験による宇宙背景放射の「まだら」のサイズの測定によって明らかになった。宇宙空間の曲率が正だと「まだら」は大きくなり、曲率が負だと「まだら」は小さくなる。詳細は本書の説明をお読みいただきたい。
![]()
![]()
- 人間原理、ランドスケープ問題、マルチバース(多宇宙)の予想。この宇宙の物理法則が少しでも違うと物質をはじめ私たちは生まれてこなかった。これは偶然なのだろうか?それとももともといろいろな物理法則で成り立つ宇宙があり、たまたま私たちは現在の宇宙に生まれたのだろうか?超弦理論やインフレーション宇宙論は、そのような多宇宙が無数に存在することを示している。なぜそう予想されるのかは本書で詳しく解説される。
マルチバース(多宇宙)の一例
![]()
超弦理論(本書では超ひも理論と表記)について言えば、クラウス博士はかなり懐疑的だ。それは「
超ひも理論を疑う:ローレンス M.クラウス」という本をお書きになっていることからもわかる。
しかし、博士は超弦理論を積極的に宣伝している物理学者ブライアン・グリーン博士とも親しく、理論に対して批判的、攻撃的な態度をとっているわけではない。やんわりと慎重な姿勢を求めているという感じだ。クラウス博士とグリーン博士の対談はYouTubeにたくさん掲載されている。お二人はとても仲がよい。
クラウス博士とグリーン博士の対談動画:
YouTubeで検索する
本書ではこのほか、2兆年先の宇宙についても予想している。宇宙はどのように終わりを迎えるのだろうか?宇宙論はそのように途方もない未来を予測することができるのだろうか?
最後になるが、宇宙やその中で働く物理法則に「創造主」はいるのだろうか?
クラウス博士は明確にそれを否定している。もし創造主がいるとしたら、その創造主はどのように生まれたのだろうか?これは2000年以上前から投げかけられてきた矛盾であり、哲学者や神学者は神の永遠性を根拠にその正当性を主張してきた。本書でクラウス博士は神学者との対話により彼らが「無」についてどのように考えているか、彼ら考え方が矛盾に満ちたものであることを解き明かしている。安易に「
神の数式」などと唱えてはならないのだ。また巻末には「著者との一問一答」が設けられ、一般的な読者が思いつくような質問に対してクラウス博士が回答を与えている。
本書を読むにあたって必要な相対性理論、量子力学などについては、必要最小限の事柄にとどめてクラウス博士は説明している。もし理解できないようならば
大栗博司先生による入門書をはじめ、ブルーバックスなどで関連本をお読みになるとよいだろう。
今回の記事で紹介したのはこの本だ。英語版だとKindleでも読むことができる。
「
宇宙が始まる前には何があったのか?:ローレンス・クラウス」
「
A Universe from Nothing: Lawrence M. Krauss」(
Kindle版)
![]()
![]()
クラウス教授の著書をAmazonで検索する:
単行本(日本語) 単行本(英語) Kindle版(英語)
参考書籍:
「
インフレーション宇宙論―ビッグバンの前に何が起こったのか:佐藤勝彦」
「
宇宙,無からの創生―138億年の仮説はほんとうか(Newton別冊)」
![]()
![]()
参考書籍2
物理学の発展と宇宙観の変遷、そして斥力としての重力について、より詳しく知りたい方は次の記事で紹介している本をお読みになるとよい。この本も青木薫さんの訳書である。
宇宙を織りなすもの(上):ブライアン・グリーン
http://blog.goo.ne.jp/ktonegaw/e/9a33e8f5ee79057972cf86c7b20c5218
宇宙を織りなすもの(下):ブライアン・グリーン
http://blog.goo.ne.jp/ktonegaw/e/e7d60b8a36b423ef5d42df59458804b7
人間原理、ランドスケープ問題、マルチバース(多宇宙)について、より詳しく知りたい方は次の記事で紹介している本をお読みになるとよい。
隠れていた宇宙(上):ブライアン・グリーン
http://blog.goo.ne.jp/ktonegaw/e/4a1abbca21c0188f43d7d72af39287f2
隠れていた宇宙(下):ブライアン・グリーン
http://blog.goo.ne.jp/ktonegaw/e/6e8b34dc9e4a3d21e82de47960f2a07d
応援クリックをお願いします!
![にほんブログ村 科学ブログ 物理学へ]()
![人気ブログランキングへ]()
![]()
![]()
「
宇宙が始まる前には何があったのか?:ローレンス・クラウス」
![]()
まえがき 宇宙は無から生じた
はじめに 何もないところから、何かが生まれなくてはならない
第1章 いかに始まったのか?
始まりの一秒。百億度のプラズマ状態。陽子と中性子が結びついては、さらなる衝突のためにふたたびバラバラになる。ビッグバンモデルでさかのぼる原初の宇宙の状態とは。
第2章 いかに終わるのか?
「開いた宇宙」「閉じた宇宙」「平坦な宇宙」のいずれかで、終末のシナリオは3つある。この予想の鍵を握るのが、目に見えない大量の暗黒物質(ダークマター)だ。その正体を捉えることはできるのか。
第3章 時間の始まりからやってきた光
生まれて間もない高温の宇宙で発せられた光の残照、それが宇宙マイクロ波背景放射である。宇宙誕生の瞬間を見ることは不可能だ。しかし誕生から30万年後の姿は見ることができる。
第4章 ディラックの方程式
ミクロなスケールの世界を記述する量子力学。そこでは何もないところから仮想粒子が生成消滅する。特殊相対性理論と量子力学を結び合わせたディラックは、宇宙の始まりにも関係する重大な発見をする。
第5章 99パーセントの宇宙は見えない
エネルギーを含んだ空っぽの空間の中に、「暗黒物質(ダークマター)」の海があり、わずか1%の目に見える物質がその海の中に浮かんでいる。それが現在の物理学が到達した宇宙像なのである。
第6章 光速を超えて膨張する
われわれに観測可能な宇宙も、膨張の速度が加速し、やがて光速を超える。アインシュタインが課した制限速度も、空間そのものにはあてはまらない。
第7章 2兆年後には銀河系以外は見えなくなる
宇宙がこのまま膨張し続けると、2兆年後にはすべての天体が遠ざかり姿を消す。ビッグバンの手がかりも消えるだろう。われわれは宇宙を観測できる貴重な時代を生きている。
第8章 その偶然は人間が存在するから?
インフレーションモデルやひも理論によると、宇宙はひとつではなく無数に存在するという。とするとわれわれの宇宙は、人間が存在するのに適した宇宙に過ぎないのではないか。
第9章 量子のゆらぎ
現在の量子力学は、何もない場所に量子のゆらぎが生じ、あらゆる構造を生むことを説明する。つまり何もない場所が何らかのエネルギーを持つことができるということだ。
第10章 物質と反物質の非対称
量子力学と相対性理論によれば、物質に対応する反物質は必ず存在し、それらは打ち消しあう。しかしビッグバンの最初の状態では、わずかな非対称があった。それがわれわれを生んだのだ。
第11章 無限の未来には
何もない場所から、何かが常に生まれている。しかし、おそらく遠い未来には、無がふたたび宇宙を支配することになりそうだ。
あとがき リチャード・ドーキンス
訳者解説 青木薫