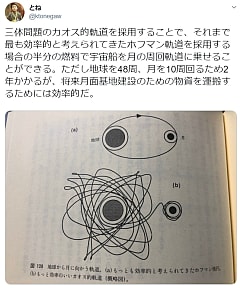
毎年12月10日、スウェーデンのストックホルムでアルフレッド・ノーベルの命日に行われるノーベル賞の授賞式の日程にあわせて、「とね日記賞」を発表している。今年で10回目。
ノーベル賞を僕がもらう見込みはどうもなさそうだ。ならば自分で賞を作って「あげる側」になってしまえ!という思いつきだ。
「とね日記賞」はその年に読んだ物理学書、数学書の中から自分のためになった本、この分野を勉強している学生や社会人にお勧めする本を物理学、数学など各分野に分けてそれぞれ1~2冊発表する。あとテレビドラマ賞や贈り物にふさわしい本としてクリスマス賞も設けている。
名著であっても僕がその価値を理解できなければ受賞できない。昨年以前に読んだ本は自動的に選考対象から外されるし、どんなに良書であっても読んでいなければ対象外。何より僕の学習進度や理解度や好みに影響される。
メダルも賞金も授賞式もスピーチも晩餐会も舞踏会もないから、ありがたくも何ともなく、主観だらけのアンフェアな賞だ。
今年は次の賞を発表する。今年から「洋書賞」を設けることにした。
- 物理学賞
物理学の教科書、専門書から選考。
- 天文学賞
物理学の教科書、専門書から選考。
- 数学賞
数学の教科書、専門書から選考。
- 洋書賞
洋書の教科書、専門書、科学教養書から選考。
- AI賞
AIに関する本から選考。
- 教養書賞
一般向け書籍から分野別に選考。
- 新人賞
書籍出版デビューを果たした方が書いた本から選考。
- 功労賞
科学史への貢献、ライフワークを完結されたような本から選考。
- 文学賞
ジャンルを問わない小説、文学書から選考。
- アカデミー賞
今年観た映画の中からよかったものを選考。
- テレビドラマ賞
テレビドラマの中からよかったものを選考。
- クリスマス賞
クリスマスプレゼントにふさわしい本を選考。
この1年で読んだ本は53冊で、次のような本である。通算381冊~433冊目。(参考:「
400冊の理数系書籍を読んで得られたこと」)
381/ブラックホールと時空の方程式:15歳からの一般相対論:小林晋平
382/はじめて学ぶリー環: 井ノ口順一
383/力学の誕生―オイラーと「力」概念の革新―: 有賀暢迪
384/よくわかる初等力学: 前野昌弘
385/高校生からわかる複素解析: 涌井良幸
386/量子と情報 ―量子の実在と不確定性原理―: 小澤正直
387/科学者はなぜ神を信じるのか コペルニクスからホーキングまで : 三田一郎
388/完訳 天球回転論: ニコラウス・コペルニクス
389/星界の報告: ガリレオ・ガリレイ
390/テレポーテーション 瞬間移動の夢: デヴィッド・ダーリング
391/楕円関数入門: 戸田盛和
392/数理解析のパイオニアたち: V.I.アーノルド
393/天体力学のパイオニアたち 上: F.ディアク、R.ホームズ
394/天体力学のパイオニアたち 下: F.ディアク、R.ホームズ
395/ポアンカレ 常微分方程式 -天体力学の新しい方法-
396/核兵器: 多田将
397/線型代数学(新装版):佐武一郎
398/ザイマン現代量子論の基礎(新装版):J.M.ザイマン
399/テンソル解析:田代嘉宏
400/なっとくする群・環・体:野崎昭弘
401/ブラックホールと時空の歪み: キップ・S. ソーン
402/神は老獪にして…: アブラハム・パイス
403/ホーキング、ブラックホールを語る:BBCリース講義
404/巨大ブラックホールの謎 宇宙最大の「時空の穴」に迫る: 本間希樹
405/ゼロからわかるブラックホール: 大須賀健
406/ビッグ・クエスチョン―〈人類の難問〉に答えよう:スティーヴン・ホーキング
407/ホーキングとペンローズが語る 時空の本質―ブラックホールから量子宇宙論へ
408/宇宙と宇宙をつなぐ数学 IUT理論の衝撃: 加藤文元
409/ガロア―天才数学者の生涯 (中公新書): 加藤文元
410/一般相対性理論入門 ブラックホール探査: テイラー、ホイーラー
411/一般相対論の世界を探る―重力波と数値相対論:柴田大
412/アインシュタインここに生きる: アブラハム・パイス
413/難しい数式はまったくわかりませんが、微分積分を教えてください!: たくみ
414/はじめて学ぶ物理学 上 学問としての高校物理: 吉田弘幸
415/はじめて学ぶ物理学 下 学問としての高校物理: 吉田弘幸
416/予備校のノリで学ぶ大学数学: ヨビノリ たくみ
417/力学系カオス: 松葉育雄
418/幾何学から物理学へ: 谷村省吾
419/ディープラーニングと物理学 原理がわかる、応用ができる:田中章詞、富谷昭夫、橋本幸士
420/相対論とゲージ場の古典論を噛み砕く: 松尾衛
421/ベクトル解析30講:志賀浩二
422/具体例から学ぶ 多様体:藤岡敦
423/Hirsch・Smale・Devaney 力学系入門 ―微分方程式からカオスまで― 第3版
424/QED: The Strange Theory of Light and Matter: Richard P. Feynman
425/龍雄先生の冒険 回想の内山龍雄:一般ゲージ場理論の創始者
426/時間は存在しない: カルロ・ロヴェッリ
427/量子情報と時空の物理 第2版: 堀田昌寛
428/The Order of Time: Carlo Rovelli(時間は存在しない)
429/Lumière et matière - Une étrange histoire: Richard P. Feynman(光と物質のふしぎな理論)
430/Surely You're Joking, Mr. Feynman!(ご冗談でしょう、ファインマンさん)
431/数学的な宇宙 究極の実在の姿を求めて: マックス・テグマーク
432/物理学者,機械学習を使う ー機械学習・深層学習の物理学への応用ー
433/高次元空間を見る方法: 小笠英志
今年の科学ニュース、科学出版界を象徴するキーワードは「ブラックホールと一般相対性理論、深層学習」、「物理学と深層学習、機械学習」、「IUT理論」の3つの組み合わせだと思う。
それでは2019年の「とね日記賞」を発表しよう。(書籍名と画像は本の購入ページにリンクさせておいた。)
* 物理学賞
この2冊に授賞することにした。
「
神は老獪にして…: アブラハム・パイス」
![]()
授賞理由: 今年の4月に新聞一面のトップを飾ったのがブラックホールを直接撮影した画像だった。これが本当に正しい画像なのかは今後も精査されるようだが、ビッグニュースには違いない。そしてこの画像を得るのに使われたのが深層学習である。かのアインシュタインさえその存在に否定的だったブラックホールの姿はものすごいインパクトがある。そしてその存在の予言のもとになったのが一般相対性理論だ。本書はこの偉大な理論を構築したアインシュタインのいちばん詳しく、正確な伝記本である。数式も躊躇なく使っているため専門書として授賞させていただいた。
紹介記事は次のリンクからお読みいただきたい。
神は老獪にして…: アブラハム・パイス
https://blog.goo.ne.jp/ktonegaw/e/d9258ed7a2d52173116ccd6e61ba0881
そして物理学賞の2冊目はこの本である。
「
Hirsch・Smale・Devaney 力学系入門 ―微分方程式からカオスまで― 第3版 」
![]()
授賞理由: 未来が不確定、予測不可能であること根拠は量子力学だけでなく、古典力学にもある。これに初めて気がついたのはフランスの数学者、アンリ・ポアンカレで彼が三体問題の微分方程式の解を研究していたときのことだった。(参考記事:「
ポアンカレ 常微分方程式 -天体力学の新しい方法-」)その後、この研究領域は「
力学系」と呼ばれるようになり現在も発展中である。力学系、カオス、複雑系の本は昨年秋以降、何冊も読んだが本書はその入門的な専門書としていちばんお勧めできる本である。力学系は本来は微分方程式を扱う数学の領域であるが、その発端が天体力学の研究にあったこと、物理的領域への応用が広いことから物理学の専門書として授賞させていただいた。
紹介記事は次のリンクからお読みいただきたい。
Hirsch・Smale・Devaney 力学系入門 ―微分方程式からカオスまで― 第3版
https://blog.goo.ne.jp/ktonegaw/e/98d451af90b7efc63aacbe4efdb330fa
* 天文学賞
「
一般相対性理論入門 ブラックホール探査: テイラー、ホイーラー」
![]()
授賞理由: 今年のメインテーマのブラックホールの物理を解説した本。まるで自分がブラックホール探査をしているような気分になることができ、とてもワクワクしながら読める専門書である。ブラックホールはその質量や回転の有無によってその周囲の力学的状況が変化するが、その様子を計算して見せてくれる本だ。タイトルには「一般相対性理論入門」と書かれているが、この理論を初歩から解説する本ではなく「一般相対性理論をブラックホールに応用する本」である。(ただし微積分と特殊相対性理論の初歩は解説される。)翻訳のもとになった原書の初版が刊行されたのは2000年。(日本語版刊行は2004年)解析的に求める計算に加え、その当時のコンピュータで計算できる範囲でのブラックホール探査シミュレーションを例示して学ぶことができる。つまり当時よりずっと性能が上がった現代の自分のパソコンで計算できるわけだから、興味がいっそうかき立てられるのだ。ニュートン力学での計算結果と一般相対性理論での計算結果の違いを図やグラフで示しているのがよいところ。そしてその後改訂され2016年に刊行された原書第2版は、著者のおひとりのテイラー博士のホームページから最新版のPDFファイルを無料でダウンロードできるのもありがたい。(現在の最新版は2019年4月8日版)著者ホームページへのリンクは、本書の紹介記事に記載しておいた。
紹介記事は次のリンクからお読みいただきたい。
一般相対性理論入門 ブラックホール探査: テイラー、ホイーラー
https://blog.goo.ne.jp/ktonegaw/e/c928268aab686a527be93385b45402c2
* 数学賞
この2冊に授賞することにした。
「
線型代数学(新装版):佐武一郎」
![]()
授賞理由: たとえ読んでいないとしても、この教科書を知らない人は数学徒を名乗ってはならない。2006年には日本数学会出版賞を受賞した。読みやすい新装版が刊行された2015年に購入したが、今年ようやくこの名著を読むことができた。線形代数学をひととおり学んだ人が、2冊目、3冊目に学ぶためにお読みいただきたい。線形代数学を初めて学ぶという方には、本書は敷居が高すぎるため
2016年のとね日記賞で数学賞を授賞させていただいた「
線型代数[改訂版]: 長谷川浩司」のほうをお勧めする。
紹介記事は次のリンクからお読みいただきたい。
線型代数学(新装版):佐武一郎
https://blog.goo.ne.jp/ktonegaw/e/68045ac328ae84567ee61c91f03bb99e
そして数学賞の2冊目はこの本である。
「
具体例から学ぶ 多様体:藤岡敦」(
Kindle版)(
サポートページ)
![]()
授賞理由: 微積分や線形代数もそうだが、多様体の入門書や教科書についてもこれまで数多くの良書が刊行されているため、このテーマで新しい本を書くのはハードルが高い。タイトルと表紙に惹かれていたことと、SNS上での人気が気になってKindle版を購入して読んでみた。結果的には読んで大正解。大学初年度の理系学徒が、多様体の世界にスムーズに入るために格好の本だと思う。ただし、あくまでも本書は多様体理論の導入部分、初歩の初歩を図を活用しながら解説した本であることにご注意いただきたい。その後、さらに学ぶ方のために巻末に掲載されている「読者のためのブックガイド」がとても役に立つ。「
多様体の基礎: 松本幸夫著」の前にお読みになっておくとよいと思う。
紹介記事は次のリンクからお読みいただきたい。
具体例から学ぶ 多様体:藤岡敦
https://blog.goo.ne.jp/ktonegaw/e/c4be60f615dd45e67aa39e1d8d41e8ab
* 洋書賞
「
QED: The Strange Theory of Light and Matter (2006): Richard P. Feynman」
(
Kindle版)(
2014)(
1986)
![]()
![]()
![]()
授賞理由: 英語で科学教養書を読んでみたいという方のために、いちばんお勧めしたい本である。すでに刊行されている文庫本で1冊の
日本語版でお読みになってもよいわけであるが、ファインマン先生の本の中で、僕がいちばん好きな本だ。ファインマン先生が研究を続けてきた「量子電磁力学(QED: Quantum Electrodynamics)がテーマだ。主な研究対象は光子と電子、そしてその相互作用である。先生が1965年に受賞したノーベル物理学賞も電子についての「繰り込み理論」であり、ファインマン先生が考案した「経路積分」そして「ファインマン図による計算」という手法を含めて量子電磁力学に含まれる。本書は
フランス語版も読んで紹介記事を書いている。
英語版の紹介記事は次のリンクからお読みいただきたい。紹介記事は日本語で書いている。
QED: The Strange Theory of Light and Matter: Richard P. Feynman
https://blog.goo.ne.jp/ktonegaw/e/1860569fe58727fce5256356863001f9
* AI賞
「
ディープラーニングと物理学 原理がわかる、応用ができる:田中章詞、富谷昭夫、橋本幸士」(
Kindle版)(
参考書籍)
「
物理学者,機械学習を使う ー機械学習・深層学習の物理学への応用ー」
![]()
![]()
授賞理由: 物理学のいくつかの領域で深層学習、機械学習が研究に使われ始めている。これら2冊の姉妹本は、この新しい領域の物理学研究の手法を日本で初めて紹介した本である。発売前からSNSでは話題になっており、著者も予想していなかったほどの売れ行きだった。しかしながら、本書は取り上げられている物理学の各分野を学んでいることを前提とすること、深層学習や機械学習の知識をある程度必要とすることから、内容を理解できる読者が限られる。この弱点を補うために著者が勧める「参考書籍」が欠かせない。コンピュータを使った物理学研究の最前線と将来に思いをはせたい方は、ぜひチャレンジしてみてほしい。
紹介記事はそれぞれ次のリンクからお読みいただきたい。
ディープラーニングと物理学 原理がわかる、応用ができる:田中章詞、富谷昭夫、橋本幸士
https://blog.goo.ne.jp/ktonegaw/e/5edea35c359ead77cf30915e9dd28bce
物理学者,機械学習を使う ー機械学習・深層学習の物理学への応用ー
https://blog.goo.ne.jp/ktonegaw/e/069b899edd696e92ffcaae55e348397e
* 教養書賞(物理学部門)
次の2冊に授賞させていただくことにした。
「
ブラックホールと時空の歪み: キップ・S. ソーン」―アインシュタインのとんでもない遺産
![]()
授賞理由: 天文学賞を授賞した「
一般相対性理論入門 ブラックホール探査: テイラー、ホイーラー」は専門書であるが、科学ファンや一般の人がブラックホールの物理学をワクワクしながら堪能したいのならば、この本がいちばんである。原書は1994年、日本語版は1997年に刊行されたが古さを感じさせない。著者はこの分野の第一人者、2017年に連星ブラックホールの初観測をしたLIGOという観測プロジェクトの推進者のソーン博士だ。本書の冒頭からブラックホールに落ちる観測者になった気分で、周囲の時間や空間、見える景色がどのように変化するか、自分自身がどのような影響を受けるかなど、ブラックホールの質量の違いに応じて自らが体験することをSF小説さながらに語ってくれる。ブラックホールの研究史が詳細に解説され、将来予定されている観測計画にいたる経緯が当事者のひとりとして語られる。そしてその予言は2015年に現実のものになり、2019年に得られたブラックホールの画像は今年最大の科学ニュースとなった。これまでのご功績に最大の経緯を払って授賞させていただく。
紹介記事は次のリンクからお読みいただきたい。
ブラックホールと時空の歪み: キップ・S. ソーン
https://blog.goo.ne.jp/ktonegaw/e/76795b03e7dc89cd08dac67dc25b73ab
2冊目はこの本に授賞する。
「
力学の誕生―オイラーと「力」概念の革新―: 有賀暢迪」
![]()
授賞理由: 年初に読んで大いに刺激を受けた縦書きの本。ニュートン力学から解析力学(一般力学)に至る力学史を詳細に解説した本である。高校物理の力学を微積分を使って解く分野を初等力学、初等力学を一般化、汎用化したものを解析力学と呼ぶが、本書で解説されるは初等力学史、解析力学史ということになる。力や運動量、運動エネルギー、位置エネルギーは高校物理でお馴染みの力学概念であるが、これらを正しく理解するまでには、科学史上の何人もの天才の頭脳をもってしてもおよそ100年間の論争が必要だったのだ。どのように彼らが誤解し、紆余曲折していたかを知ることは、理系大学生だけでなく物理を学ぶ高校生にも知っておいてほしい。発売当初に科学ファンの間で大いに話題になった。このような本にまとめるのには、とてつもない労力と時間をかけた調査が欠かせない。著者の労と本の完成度の高さに感銘を受けたので授賞させていただくことにした。
紹介記事は次のリンクからお読みいただきたい。
力学の誕生―オイラーと「力」概念の革新―: 有賀暢迪
https://blog.goo.ne.jp/ktonegaw/e/39015937594a6282316377ae34a6a240
* 教養書賞(天文学部門)
2冊に授賞させていただくことにした。
「
巨大ブラックホールの謎 宇宙最大の「時空の穴」に迫る: 本間希樹」(
Kindle版)
![]()
授賞理由: 2019年4月10日に発表された史上初のブラックホールの画像は、ニュース報道と新聞各紙でトップ扱いされ、非常にインパクトがあった科学ニュースとなった。2016年2月に発表された重力波の初観測では、連星ブラックホールの存在が証明されていたわけだが、ブラックホールの姿を想像するのと直接見るのとは大違いである。この画像を得るために世界規模で行われたEHTプロジェクトの日本でのリーダーである本間先生がお書きになったのがこの本だ。偉業を成し遂げるまでの道のりを、一般人向けにわかりやすくお書きになった科学教養書である。本が刊行されたのは、今年の発表の2年前の2017年4月だった。本書を刊行して以降、プロジェクトに没頭されることになる。「絶対に見てやるぞ!」という意気込みと夢に満ちた著作だ。数々の困難を克服され、素晴らしい成果を成し遂げられたことに祝意を示すために授賞させていただくことにした。発表されて以降、ブラックホール画像の正当性について、詳しい解析が行われている。今後の発表を待ちたい。
紹介記事は次のリンクからお読みいただきたい。
巨大ブラックホールの謎 宇宙最大の「時空の穴」に迫る: 本間希樹
https://blog.goo.ne.jp/ktonegaw/e/c847e0b9662e20720b9e6acf5cd4f370
そして2冊目はこの本。
「
星界の報告: ガリレオ・ガリレイ」(
Kindle版)
![]()
授賞理由: 今から410年前の1609年、自前の望遠鏡を月や惑星に向けたガリレイの驚きを自身でつづった貴重な観測記録。月の表面が地上と同じように凸凹だという現在では当たり前の事実は、当時としては「教会の教えに背くとんでもないこと」だった。本書は、望遠鏡の話から始まり、月、恒星、そして木星の衛星の詳細な観測記録を含む、生々しいドキュメンタリーである。本書が与えた衝撃は、やがて伝統的な宇宙観を打ち壊す動きをもたらす原動力となった。地上界と天界は摂理の異なる2つの世界ではなく、同じ法則に従っている1つの世界だという発見は「近代科学革命」をもたらし、人類の世界観を大きく変えていく。そもそも天体観測は小中学生にもわかりやすい。当たり前に思えることが実は当たり前ではなかったということに読者には気づいていただきたい。410年前の偉業に対して授賞させていただくことにした。ガリレイの異端審問に対してローマ教皇が誤りを認めて謝罪し、ガリレイが名誉を回復したのは1992年のことだった。
紹介記事は次のリンクからお読みいただきたい。
星界の報告: ガリレオ・ガリレイ
https://blog.goo.ne.jp/ktonegaw/e/2bb491710bdf48a28c30c94e1dea7b36
* 教養書賞(数学部門)
「
宇宙と宇宙をつなぐ数学 IUT理論の衝撃: 加藤文元」(
Kindle版)
![]()
授賞理由: 本書は間違いなく今年いちばん売れた科学書だと言ってよい。10月には「一般書」に対して贈られる「
第2回 八重洲本大賞」を授賞された。12月7日現在、累計25,500部が売れ第7刷(2,500部)の増版が決まったそうだ。科学教養書とはいえ、IUT(宇宙際タイヒミュラー)理論という数学の最前線を紹介した数学本が、これほど売れたのは日本で初めてのことではないだろうか?一般の人はもちろん、数学の専門家の先生でもワクワクしながら読むことができる。IUT理論を提唱した望月先生の論文は「未来から来た論文」とも言われ、数学界のみならず、世界に衝撃をもたらした。この論文は、世界で理解できるのは多く見積もっても数人、といわれるほどの難解さであり、論文の発表から6年以上たった現在もなおアクセプトに至っていないが、望月教授と、議論と親交を重ねてきた著者は、IUT理論は数学者ではない一般の人たちにもわかってもらえるような自然な考え方に根ざしていると考える。本書では、理論のエッセンスを一般の読者に向けてわかりやすく紹介。この理論の未来に夢を託したいという気持ちで授賞させていただいた。
紹介記事は次のリンクからお読みいただきたい。
宇宙と宇宙をつなぐ数学 IUT理論の衝撃: 加藤文元
https://blog.goo.ne.jp/ktonegaw/e/f77f5bd8e1b3c96acd62fba729dc9b4e
* 新人賞
2冊に授賞させていただくことにした。お二人とも科学書の出版という意味では「新人」の方である。
「
ブラックホールと時空の方程式:15歳からの一般相対論:小林晋平」(
電子版)
![]()
授賞理由: 一般相対性理論を理解したいと思う人の夢をかなえる1冊だ。とはいっても、たいていの人にとって敷居が高い理論であることには違いない。本書はその敷居をぐっと下げたと言ってよいだろう。「15歳からの」というキャッチフレーズには、少し言い過ぎかなと思ったが、本書の前半は15歳の人でもじゅうぶん理解できる。途中で挫折する人もでてくるだろうが、それでも、知識欲を持ちながら読み進める経験は貴重だと思う。落ちこぼれてしまったとしても、数年後にまた読み直せばよいのだ。本書をきっかけに科学読書の醍醐味を知ってほしい。科学読書を趣味とする一人として、その間口を広げていただいた小林先生に感謝し、授賞させていただいた。
紹介記事は次のリンクからお読みいただきたい。
ブラックホールと時空の方程式:15歳からの一般相対論:小林晋平
https://blog.goo.ne.jp/ktonegaw/e/f4401f2ce79451070b7b9c089f304315
そして2冊目はこの本である。
「
相対論とゲージ場の古典論を噛み砕く: 松尾衛」ゲージ場の量子論を学ぶ準備として
(
サポートページ)(
参考書籍)
![]()
授賞理由: 現代物理学の標準言語である「ゲージ場の量子論」を学ぶための心の準備ができることを目指した本。古典力学や電磁気学や量子力学、線型代数やベクトル解析を聞きかじったことのある読者を対象に、現代物理学における相対論とゲージ理論の考え方の基本を、微分形式やリー代数の初歩といった数学を交えながら紹介する。ゲージ場の量子論という絶壁に挑む前に読めるこのような本は、これまでに存在しなかった。執筆中の続編にも期待しながら授賞させていただくことにした。
紹介記事は次のリンクからお読みいただきたい。
相対論とゲージ場の古典論を噛み砕く: 松尾衛
https://blog.goo.ne.jp/ktonegaw/e/b0d1802a96037c9f99d92848b042e30a
* 功労賞
次の2冊に授賞させていただくことにした。
「
完訳 天球回転論: ニコラウス・コペルニクス」
![]()
授賞理由: 地動説を世界で初めて提唱した歴史的な価値をもつ本。昨年9月にはその原書と対面することができた。これまで一部を文庫化した本しか知らなかったので、これほどの大著だとは知らなかった。2年前の2017年10月には刊行されていた。このような大著を翻訳してくださった高橋先生のご尽力に対して授賞させていただく。また、今年は講談社ブルーバックスからアイザック・ニュートンの『プリンキピア(自然哲学の数学的諸原理)』が42年ぶりに復刊したことも、科学ファンの間では大ニュースとなった。(参考記事:「
ニュートンの『プリンキピア』がブルーバックスで復刊!」)
紹介記事は次のリンクからお読みいただきたい。
完訳 天球回転論: ニコラウス・コペルニクス
https://blog.goo.ne.jp/ktonegaw/e/7aea68b6797e8739ac2eddc051cc111e
そして2冊目はこの本である。
「
龍雄先生の冒険 回想の内山龍雄:一般ゲージ場理論の創始者」
![]()
授賞理由: 世間一般にはあまり知られていない内山龍雄という理論物理学者のお弟子さん方が寄稿して完成した本である。内山先生は、1954年ごろには一般ゲージ理論を完成させていたが、論文発表が1954年に定式化された楊振寧(ようしんねい)とミルズRobert L. Mills(1927―1999)によるヤン‐ミルズ理論(非可換ゲージ理論)よりも遅れたため、ノーベル賞を逃した。一般ゲージ理論は、電弱統一理論やクォーク理論に応用され、素粒子での標準的な理論となっている。一般ゲージ理論を通じて、一般相対性理論や場の理論を広めるのに寄与した。ご病気により志半ばで他界された内山先生の物理学に対するご貢献と、弟子である先生方の内山先生に対する敬愛を、広く知っていただきたく思い授賞させていただいた。
紹介記事は次のリンクからお読みいただきたい。
龍雄先生の冒険 回想の内山龍雄:一般ゲージ場理論の創始者
https://blog.goo.ne.jp/ktonegaw/e/0648122c29b8413c5e13df83ff119756
* 文学賞
「
英語と日本軍 知られざる外国語教育史:江利川春雄」(
Kindle版)
![]()
授賞理由: 文学でも小説でもない、一般書である。今年は英語民間試験や大学入試共通テストがはらむ数々の問題が取りざたされている。そして過去20年の英語教育は失敗だったことも明らかになった。そもそも日本はこれまで、外国語をどのように教育してきたのだろうか?その歴史に僕はまったく無頓着で、無知だった。本書は特に日本の軍隊における幕末から戦後の外国語教育史を紹介したものだ。もともと外国語好きであることがあり、本書はとても興味深く読むことができた。英語を学んだことがある、すべての日本人にお勧めしたい本である。
紹介記事は次のリンクからお読みいただきたい。
英語と日本軍 知られざる外国語教育史:江利川春雄
https://blog.goo.ne.jp/ktonegaw/e/f6ec131cc401ec90fb390a62bed94456
* アカデミー賞
今年は月面着陸50周年の記念すべき年だ。この偉業が達成されたのは1969年7月20日。人類の月面第一歩は世界中に生中継され、14億人が固唾を飲みながら見守っていたという。今年公開された次の2作品に授賞させていただくことにした。映画『アポロ11 完全版(2019)』は、先週ネット配信が始まったばかりである。
映画『ファースト・マン(2018)』
![]()
映画『アポロ11 完全版(2019)』
![]()
予告編動画を埋め込んだ紹介記事は次のリンクからお読みいただきたい。
映画『ファースト・マン(2018)』
https://blog.goo.ne.jp/ktonegaw/e/70be98d22d147227bc01e7d7eaa0019a
映画『アポロ11 完全版(2019)』
https://blog.goo.ne.jp/ktonegaw/e/fd06df78b3fcec05e0f287857870c8f3
* テレビドラマ賞
『家売るオンナの逆襲』、『わたし、定時で帰ります。』、『白衣の戦士!』、『G線上のあなたと私』、『ドクターX6~外科医・大門未知子~』、『時効警察はじめました』、『まだ結婚できない男』、『いだてん ~東京オリムピック噺(ばなし)~』を楽しんでいた。この中から選考するのは、とても悩ましい。しかし、めちゃくちゃ楽しめたこのドラマに授賞させていただくことにする。視聴率は芳しくないのだが、それはストーリーや会話のテンポが速く、高齢者層がついていけないためだと思われる。それでもやはりクドカンは最高だ。
NHK大河ドラマ『いだてん ~東京オリムピック噺(ばなし)~』
![]()
NHK大河ドラマ『いだてん ~東京オリムピック噺(ばなし)~』公式ページ
https://www.nhk.or.jp/idaten/r/
YouTubeの動画:
検索する
* クリスマス賞
今年は月面着陸50周年であるだけでなく、映画『男はつらいよ』50周年でもある。アームストロング船長が月面へ第一歩を踏み出した翌月の1969年8月27日に男はつらいよの第1作が公開された。以後、第49作まで日本映画史に残る国民的映画として人気を博した。
クリスマスプレゼントに寅さんの本を贈ることに、僕には何のためらいもない。寅さんを演じた
渥美清さんは1996年、お亡くなりになる直前に洗礼を受けてクリスチャンになっていたのだから。
「
男はつらいよ お帰り 寅さん」(
Kindle版)
「
知識ゼロからの寅さん入門」
![]()
![]()
50周年を記念して、12月27日に第50作目の『男はつらいよ お帰り 寅さん』が全国ロードショー公開される。またシリーズ全49作が4Kデジタル版として修復された。
映画『男はつらいよ』公式サイト
https://www.cinemaclassics.jp/tora-san/
この映画は若い人にもぜひご覧いただきたい。昭和の寛容さだけでなく、平成の間に失われた大切なものをいくつも見つけることができるはずだ。正月映画の定番である。初詣は
柴又帝釈天に参拝するとよいだろう。(参考ページ:「
ようこそ柴又参道へ」)
後藤久美子、「寅さん」撮影で吉岡秀隆に感謝
男はつらいよ 主題歌 (歌詞付き)
寅次郎、えんぴつを売る ~男はつらいよ「拝啓車寅次郎様より~
徹子の部屋 渥美清さん・倍賞千恵子さん(昭和54年)
渥美清の伝言:
YouTubeで再生
寅さんよ永遠に、渥美清さん追悼特集:
再生リスト
第1作から第49作は、ネットで配信されている。第50作の公開前に、ご覧になっておくとよいだろう。(
作品一覧)
Prime Video:
検索する
YouTubeムービー:
検索する
最後になりますが本日ストックホルムでの授賞式に臨まれる先生方、ノーベル賞受賞おめでとうございます!
2019年 ノーベル物理学賞はピーブルズ博士、マイヨール博士、ケロー博士に決定!
https://blog.goo.ne.jp/ktonegaw/e/671a733c37916c34a7f886bcbdf2c732
2019年 ノーベル化学賞はグッドイナフ博士、ウィッティンガム博士、吉野博士に決定!
https://blog.goo.ne.jp/ktonegaw/e/85f86e05e185bca7d9f0d2b958bd310b
関連記事:
過去の「とね日記賞」一覧:
開く
メルマガを書いています。(
目次一覧)
![]()
応援クリックをお願いします。
![にほんブログ村 科学ブログ 物理学へ]()
![人気ブログランキングへ]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![にほんブログ村 科学ブログ 物理学へ]()
![人気ブログランキングへ]()
![]()
![]()
![]()
![]()
![]()