「
力学系カオス: 松葉育雄」
内容紹介:
カオスという不規則な変動は、物理学、化学、生物学、応用力学、医学、経済学などの幅広い分野で観察され、利用されている。本書はそのようなカオスの理論について、基本から丁寧に解説。カオスを理解し、使いこなすために必要な、分岐現象、多様体の幾何学構造、記号力学など力学的な見方に重きをおいた。応用することを前提に、そしてイメージがしやすいように、理論と実例との対応をなるべく示した。とくに、理解に役立つよう、数値解析やグラフィックスをふんだんに用いたため、理論そのものだけでなく、理論と実現象とのつながりがよくわかる。また、演習問題や研究課題も掲載。カオス理論をこれから学ぶ理工系の方や、さらに本格的に知りたい方、利用したい方に適した1冊である。
2011年6月17日刊行、520ページ。
著者について:
松葉育雄(まつば いくお): 研究者ページ:
https://nrid.nii.ac.jp/ja/nrid/1000030251177/
1952年大阪府に生まれる。1980年東京大学大学院理学系研究科博士課程修了。1980年株式会社日立製作所入社。1993年千葉大学工学部教授。2007年千葉大学大学院融合科学研究科情報科学専攻教授。理学博士。専門は複雑系、ニューラルネットワーク、時系列解析。
理数系書籍のレビュー記事は本書で417冊目。
将来の予測が不可能なカオスという現象が存在することに科学史上初めて気が付いたのは、フランスの数学者
アンリ・ポアンカレ(1854-1912)だった。彼は天体の3体問題を解くため、微分方程式の研究を進める中で、万有引力の法則に従う天体の軌道が不規則かつ無限の数に分岐することを発見し、ホモクリニック軌道とヘテロクリニック軌道という名前をつけた。彼は1890年ごろから天体力学の研究を展開していたが、その成果は1892年、1893年、1899年に『天体力学の新しい方法(原書閲覧:
第1巻、
第2巻、
第3巻)』として出版された。カオス軌道のことが書かれている第3巻の日本語訳が2月に紹介した「
ポアンカレ 常微分方程式 -天体力学の新しい方法-」である。
科学がどんなに進歩しても量子力学の「
不確定性原理」は、物体の運動の未来が不確定で予測不能であることを理論的に示している。(参考記事:「
鉛筆はどれくらいの時間立っていられるか?」)しかし、ポアンカレは1912年に亡くなっているから前期量子論をぎりぎり知り得る状況にあったが、量子力学が誕生して間もない1927年に発表された不確定性原理のことは知り得ない。ボルンの「
確率解釈(1926年)」や「
神はサイコロを振らない(1926年)」というアインシュタインの言葉も聞くことはなかった。
もちろん将来が予測できないことははるか昔から、つまりコイン投げやサイコロ投げで賭け事を始めたころには知られており、確率論は16世紀から17世紀にかけてカルダーノ、パスカル、フェルマー、ホイヘンス等によって数学の一分野としての端緒が開かれていた。フランスの数学者・天文学者
ピエール=シモン・ラプラス(1749-1827)は1814年に『確率の哲学的試論(
原書閲覧)』(日本語訳:「
確率論 -確率の解析的理論-」)を書いている。
つまり、ポアンカレの時代には確率的な現象が知られていたが、それは人間の技術や測定の限界からおきるのであって、もしサイコロの形が正確にわかり、投げるときの持ち方、投げる方向、スピード、サイコロが転がる面の形状が決まっていれば予測できるのだと信じられていた。ニュートン力学に従う古典力学の問題である。
古典力学はニュートンの運動方程式 F=ma で示されるように未来を完全に予測し、決定論が正しいことを示している。小学校の算数で習う「距離=速さx時間」は x=vt のことだから、これは私たちが人生で最初に出会う決定論の公式だ。
このように天体の3体問題は純粋に古典力学で解くべき問題、連続力学系を微分方程式で解く問題である。カオスを発見したポアンカレの驚きは、とてつもないものだったことだろう。それは著書の中の「3体問題がいかに複雑なものか、またこの問題を解くためには、われわれの既知の知識とは異なった超越的な知識がいかに必要であるかもわかってくる。」や「その複雑さは驚くべきもので、私自身もこの図形を引いてみせようとは思わない。」という文章に現れている。
しかし、彼の人生は短すぎた。さぞ悔しかったことだろう。カオスの深い謎の探究は、次の世代の数学者たちに委ねられた。その後の研究・発展の歴史は「天体力学のパイオニアたち : F.ディアク、R.ホームズ(
上巻、
下巻)」という本の紹介記事として書いている。
物理学や数学は「なぜ人間は生きているのか?」と同じ意味合いで「なぜ未来は決まっていないのか?」という問いには答えてくれない。けれども「未来が決定しないことが生じるのは、どのような仕組みによるものか?」という問いには答えることができる。量子力学の不確定性原理に加え、カオスは未来を予測不能にしている原因のひとつなのである。
前置きが長くなってしまったが、本書「
力学系カオス: 松葉育雄」を読んだのは、カオスのその後の研究成果を数式を使った形で詳しく知りたくなったからである。
読み始めたのはゴールデンウィークが明けてすぐだったが、大判の本で520ページもあるから難儀した。先日ようやく読み終えることができた。具体例が豊富で、数式だけでなく図版やコンピュータによるシミュレーション結果がその都度示されているから、初めて読む専門書としては最適だと思う。
章立てと、各章の内容は次のとおりだ。
第1章 微分方程式と力学系
カオスを理解するためには、微分方程式と力学系に関する基礎を理解していなければならない。力学系とは、状態が時間の経過とともに変化するシステムのことである。力学系は微分方程式で表される連続力学系と、差分方程式で表される離散力学系に分けられるが、ほとんどの場合、両者を区別することなくカオス理論を展開できる。自然現象を対象にする場合は、おもに微分方程式を扱うので、連続力学系に関する基本的な概念から先に述べ、その後で離散力学系に進む。
本章で扱ういくつかの例はカオスではないが、力学系の基礎概念を把握するために適切と思われるシステムを選んだ。また、カオスの例としてファンデルポール方程式と呼ばれる非線形微分方程式をとりあげるが、これを用いてカオスの中核をなす部分にまで踏み込んで説明する。カオス理論を説明する前に、本書の最初の章でカオスの具体例をとりあげる理由は、「こういうふうに調べていけば、なぜカオスという不規則な変動が生まれるかが理解できるようになる」という雰囲気を味わってほしいからである。ただし、その背景になる力学構造などは気にしないで、読み進めてほしい。ここで力学構造とは、力学系の挙動を決定する方程式の幾何学的な構造の総称で、詳しくは第2章で説明する。
本章と続く第2章は、力学系を語るためのいろいろな言葉を導入する役割も果たしているが、力学系を一通り勉強した読者もぜひ目を通してもらいたい。
キーワード: 連続力学系、微分方程式、初期値鋭敏性、相空間と軌道、相図、ダッフィング方程式、セパラトリックス、自律系と非自律系、離散力学系、線形写像、エノン写像、ポアンカレ写像、ポアンカレ断面、平衡点、周期軌道、クモの巣図、ファンデルポール方程式、強制ファンデルポール方程式、極限閉軌道、アトラクター、引き伸ばしと折り畳み、抽象化写像による記号化、記号力学系、鞍点、渦状点、渦心点、双曲型、ロトカ・ボルテラ方程式
第2章 力学構造
本章では、力学系の概念をさらに押し進め、数学的に正確な言葉を用いて力学構造を調べるための基礎知識を述べる。どれも重要な概念ばかりであり、それらの意味は十分理解してほしい。とくに、位相共役性を基礎にした力学系の等価性に関する概念は、カオスを理解するためにはどうしても必要になる。たとえば、第1章で述べたように、平衡点近傍での挙動を考えると、平衡点が双曲的ならば線形化近似によってもとの力学系の特徴をとらえることができる。このことを、力学的に等価、あるいは位相的に等価であると表現する。このような等価性は任意のシステムに拡張することができ、これにより構造安定性という重要な概念が導かれる。
キーワード: 位相共役性、位相的等価性、多様体、微分多様体、力学構造、トーラス、微分同相写像、位相共役写像、線形システム、双曲性、不変多様体と局所不変多様体、安定多様体、不安定多様体、中心多様体、ヘテロクリニック軌道、ホモクリニック軌道、サドル接続、線形安定性と非線形安定性、ダッフィング方程式、極限集合、漸近挙動、非遊走集合、ポアンカレ・ベンディクソンの定理、吸引集合、アトラクター、構造安定性
第3章 カオスの例と特徴
本章では、カオス的な不規則変動の特徴をシステムが示す異なる側面から探り、カオスとはいったい何か、またカオスがどのような特徴をもっているか、といった疑問に対して、実例を用いて答えたい。とくに重要な概念である初期値鋭敏性、分岐、記号化、多様体などについて数値的に調べる。カオスの力学構造を理解するための厳密な理論は次章以降で述べるが、ここではまずは現象としてカオスを把握してほしい。本章でとりあげる例は力学、電気回路など、いずれも学部学生にも馴染みのあるものばかりである。モデルの導出のみならず、シミュレーションも実行してほしい。
キーワード: 初期値鋭敏性、2重振り子、ラグランジュの方程式、概周期軌道、リャプノフ指数、一般化ベーカー写像、ロジスティック写像、磁石振り子、フラクタル吸引領域、フラクタル次元、マンデルブロ集合、ジュリア集合、分岐、チュア回路、局所的分岐、大域的分岐、周期倍分岐、分岐図、リターンマップ、ホモクリニック軌道、ホジキン・ハクスレイ方程式、ホップ分岐、極限閉軌道、ヒステリシス、ポアンカレ写像、記号化、古典的散乱、軌道の記号化と位相的推移性、旅程、カントール集合、馬蹄、ストレンジアトラクター、制限3体問題、遅延微分方程式
第4章 局所的分岐
分岐とは、システムのパラメータを変化させるとその力学構造が大きく変わるような現象である。古くはTomによりカタストロフ理論として体系化され、工学、物理学、生態学、心理学などさまざまな分野で応用されてきた。カオスという不規則な挙動を生むメカニズムを理解するためには、非線形システムの大域的な分岐を理解することが必要であるが、そのためにはまず、従来からよく知られている局所的分岐からはじめなければならない。局所的分岐は第1章で述べた線形解析ではとらえきれない非線形な挙動をとりこむという意味において、大域的な解析の第一歩である。非線形システムの平衡点近傍での挙動は、双曲型であれば、その周りで線型化したシステムによってその大まかな挙動はとらえることができた。しかし、非双曲型ならば線形化では不十分で、非線形項まで考慮しなければならない。このときに有効な方法に中心多様体理論がある。局所的分岐はおもにピッチフォーク分岐、サドルノード分岐、安定性交替型分岐、ホップ分岐に分類できる。本章では、実例をとりいれながら、これらの分岐について説明する。
キーワード: 局所的分岐、大域的分岐、ヒステリシス、ピッチフォーク分岐、ポテンシャル関数、リャプノフ関数、安定と漸近安定、リャプノフ指数、サドルノード分岐、超臨界サドルノード分岐、亜臨界サドルノード分岐、安定性交替型分岐、超臨界ピッチフォーク分岐、亜臨界ピッチフォーク分岐、周期倍分岐、中心多様体定理、高次元システムの分岐、ホップ分岐、超臨界ホップ分岐、亜臨界ホップ分岐、ナイマルク・サッカー分岐、ローレンツモデル、Zeemanの機械、ギャロッピング
第5章 大域的分岐
第4章の局所的分岐では、平衡点近傍に限った局所的な解析で十分で、せいぜい中心多様体を決めることが必要になったくらいである。しかし、大域的分岐では平衡点近傍に限らず、大域的な挙動の解析が必要になる。とくにカオスを出現させる基本的な分岐として、同一の平衡点を結ぶホモクリニック軌道の分岐、異なる平衡点を結ぶヘテロクリニック軌道の分岐が重要で、本章ではこれらの分岐をまとめて大域的分岐とよんでいる。両軌道をまとめて、サドル接続という。大域的分岐はカオスを導く過程であり、それゆえカオスがどのような機構を通じて発生するのかも明らかになる。この機構を記述する力学系が記号力学系で、第6章で述べる。本章ではおもに2次元および3次元システムを対象として、分岐点を計算するためのメルニコフの方法についても述べる。
キーワード: サドル接続、ホモクリニック軌道、ハミルトン系、ハミルトン関数、リャプノフの渦心定理、ヘテロクリニック軌道、2次元サドル分岐、ホモクリニック分岐、チュア回路のホモクリニック軌道、振動系のヘテロクリニック分岐、3次元ホモクリニック分岐、3次元サドル分岐、シルニコフの定理、サドル・フォーカスホモクリニック分岐、離散力学系の分岐、非強制ダッフィング振動子の解析解、楕円関数、減衰強制ダッフィング振動子、ファイゲンバウムの普遍定数、ポアンカレ写像の構成、リューヴィルの定理、前乱流、カントール集合、馬蹄、馬蹄形写像、不変集合、メルニコフの方法、メルニコフ関数、シャルコフスキーの定理
第6章 記号力学系
サドル分岐を研究することにより、カオス的な不規則な変動を生じるメカニズムが明らかになった。それは、分岐後に現れるカントール集合からなる双曲型不変集合、つまり馬蹄であった。力学系がカオスであるための条件を考えると、実際の軌道がそれらの条件を満たしているかどうかを直接確認できることはまれである。ここで重要になるのは、位相共役写像による力学系の等価性、つまり、直接力学系を調べるのではなく、その力学系に等価な別の力学系を考えることである。等価な力学系の性質があらかじめわかっていれば、カオスかどうかの判断を容易に下すことができる。そのような目的で利用される力学系が記号力学系で、それが定義される記号列空間は双曲型不変集合と同じ役割をもつ。
キーワード: 錯綜、ホモクリニック錯綜、ヘテロクリニック錯綜、ラムダの補題、不動点、引き伸ばしと折り畳み、馬蹄の形成、スメールの馬蹄形写像、双曲型不変集合、カントール集合の記号化、二進展開、三進展開、三進集合、稠密性、馬蹄の記号化、両側無限列、片側無限列、記号列空間と記号力学系、距離空間、コンパクト、集積点、連続、シフト写像、二倍写像、パイこね変換、旅程、馬蹄と記号列空間の位相共役性、非周期軌道、位相推移的、初期値鋭敏性、ホモクリニック軌道、安定集合と不安定集合
第7章 カオス
第3章では、実例を通じてカオスの全体像を明らかにした。とくに初期値鋭敏性は数値的に容易に確認できる点で有用であるが、これだけではカオスかどうかの判断はできない。これまでの章では、「カオスとは何か」という問いに対する数学的な回答を回避しながら、カオスの実像をいろいろな角度から観察してきた。あえてそうしてきたのは、専門家によってカオスの定義が微妙に異なること、また、定義の違いによってこれまで知られているカオスがカオスでなかったというような例はないこと、そして何より、数学的な定義を実システムに当てはめることの困難さによる。
しかし、第6章の馬蹄形写像一般論は、抽象化されているがゆえにそこから得られたカオスの定義は受け入れやすい。馬蹄形写像は双曲型不変集合をもち、それは記号列空間に写像でき、記号力学系を導く、記号力学系のもつ性質をカオスの定義とするのである。そこで、本章では「カオスとは何か」という問いに対して、これまで述べてきたことを整理し、カオスが満たすべき条件を詳細に検討する。
キーワード: 2重振り子、チュア回路、古典的散乱、減衰強制ダッフィング振動子、エノン写像、ロジスティック写像、双曲型トーラス自己同型写像、二倍写像、Devaneyの定義、位相的推移性、稠密性、初期値鋭敏性、テント写像、ストレンジアトラクター、双曲型不変集合、アーノルドの猫写像、層葉、マルコフ分割、構造安定性、ファンデルポール方程式の相図、横断性、セクターバンドル、安定セクターバンドル、不安定セクターバンドル、不動点、分岐図、アトラクター、馬蹄、モース・スメール微分同相写像、シュワルツ微分、標準写像
本書に掲載されている図版、コンピュータによるシミュレーション図をいくつか紹介しておこう。
ポアンカレ断面の構成
![]()
非線形システムの多様体、ヘテロクリニック軌道
![]()
ホモクリニック軌道
![]()
減衰ダッフィング方程式の吸引領域
![]()
磁石振り子、平衡点のフラクタル的な吸引領域
![]()
馬蹄、安定集合と不安定集合
![]()
ロジスティック写像の分岐図
![]()
「磁石振り子」によって現れるカオス軌道とフラクタル図形
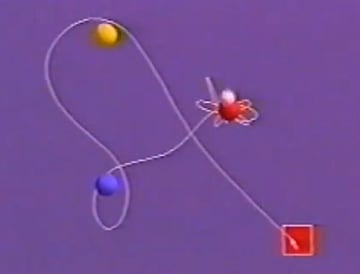
本書で取り上げられている例は、どれも興味深いものだが、ひとつだけ紹介しておこう。「磁石振り子」によって現れるカオス軌道とフラクタル図形である。
まず、このような装置を用意する。N極を上にした3つの磁石(赤、青、黄)を平面に固定し、上に鉄球(白)を振り子として吊るす。3つの磁石はどれも鉄球を引っ張っている状態だ。
![]()
磁石が1つしかないときは、磁場は(力が逆2乗の法則に従う)ニュートンの万有引力の法則のように円形になるはずだが、磁石が3つあるとそれぞれが反発しあうから、磁場すなわち磁力が等しい線(緑)と磁力線(赤)はこのような形になっているはずだ。(前野先生による
このページをお借りして3つの正電荷の場合を想定して図を作成した。)
![]()
白球(鉄球)を横に引っ張って静止させ、手を離す。磁石がなければ通常の振り子の運動をするわけだが、磁石があるから白球は複雑な軌道で振れて、最後は3つの磁石のうちの1つに吸引されて止まる。
![]()
上の図は右下の赤い四角の位置で白球から手を離したときの図だ。複雑な軌道を描いてから、白球は赤い磁石で止まることを意味している。赤い磁石で止まったから、白球の初期位置を赤い四角に塗ったわけである。
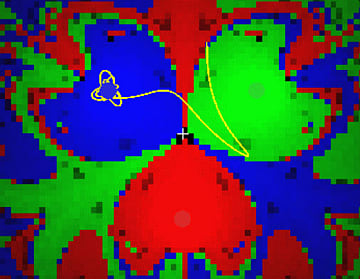
同じことを白球の初期位置を変えて何度も行う。平面上は赤、青、黄の四角で塗りつぶされることになる。動画でご覧いただきたい。(再生時間7分)
カオス、フラクタルという数学と物理学の関係
初期位置をわずかに変化させるだけで、軌道や最終位置が大きく変化することがおわかりになるだろう。これはカオス現象に必要な条件のひとつ「初期値鋭敏性」をあらわしている実験だ。最終的にこのような赤青黄が入り組んだ複雑な「
フラクタル図形」が得られる。有名な「
バタフライ効果」も初期値鋭敏性を示すカオス現象だ。
拡大
![]()
次のページではホームページに組み込まれたプログラムを使って、自分で実験することができる。初期位置にマウスポインタを置くと、白球が描く軌道がリアルタイムに描かれるので試していただきたい。(スマホではダメ。PCでのみ試せることを確認した。)
試してみる
![]()
この磁石振り子(magnet pendulum)はカオス現象の一例であり、(百円ショップで買える道具を使って)実際に実験できるだけでなく微分方程式をコンピュータで解いて得られる古典力学の問題であることを強調しておきたい。
専門書の紹介
カオス現象はいくつも種類があるが、スメール博士によって考え出された「馬蹄(ばてい)」のアイデアにより「
カントール集合」と呼ばれる離散的な無限集合を含んでいることが発見された。馬蹄とは馬の足につけるU字型をした蹄鉄のことである。そしてカオスを「無限小数」に記号化して表現、計算することが可能になり、研究に進展をもたらした。「カントール集合」が比較的シンプルな微分方程式の解に、そして現実の物理現象にあらわれるとは、僕には驚きだった。しかし、現実の物理現象は不確定性原理にも支配されているから、カントール集合であらわされる無限小の力学的ポテンシャルには限界があるはずだと僕は予想している。カオス理論は力学系を研究する数学なのだ。
「
馬蹄への道: 2次元写像力学系入門: 山口喜博、谷川清隆」
![]()
カオスを含め、この分野は「
力学系」として分類される。馬蹄の発案者であるスメール博士がお書きになった、定番の教科書はこちら。最新の第3版の日本語版は2017年に刊行されたばかりだ。
「
Hirsch・Smale・Devaney 力学系入門 ―微分方程式からカオスまで― 第3版」(
第2版)(
初版)
![]()
同書の英語版はこちらである。
「
Differential Equations, Dynamical Systems, and an Introduction to Chaos, Third Edition 3rd Ed」(
Kindle Ed)(
2nd Ed)(
1st Ed)
![]()
力学系の本:
Amazonで検索
カオスの本:
Amazonで検索
教養書の紹介
カオスや力学系全般を数式なしで解説した教養書は、まだ読んでいないが、次のような本がよさそうである。ほかにお勧めの本をご存知の方は紹介していただきたい。
「
カオス的世界像―非定形の理論から複雑系の科学へ: イアン スチュアート」
「
カオスとフラクタル (ちくま学芸文庫): 山口昌哉」
![]()
![]()
一風変わったところでは、この本が面白いかもしれない。
「
カオスの紡ぐ夢の中で: 金子邦彦」
![]()
関連記事:
ポアンカレ 常微分方程式 -天体力学の新しい方法-
https://blog.goo.ne.jp/ktonegaw/e/88846fbb12ed1f8b11a49f0659b93c75
天体力学のパイオニアたち 上: F.ディアク、R.ホームズ
https://blog.goo.ne.jp/ktonegaw/e/5c51d50e2141c8ae58c9323ad49b65a1
天体力学のパイオニアたち 下: F.ディアク、R.ホームズ
https://blog.goo.ne.jp/ktonegaw/e/88846fbb12ed1f8b11a49f0659b93c75
数理解析のパイオニアたち: V.I.アーノルド
https://blog.goo.ne.jp/ktonegaw/e/165c894d023b1174fd519522935cdeeb
メルマガを始めました。(
目次一覧)
![]()
応援クリックをお願いします。
![にほんブログ村 科学ブログ 物理学へ]()
![人気ブログランキングへ]()
![]()
![]()
![]()
![]()
![]()
「
力学系カオス: 松葉育雄」
![]()
まえがき
第1章 微分方程式と力学系
1.1 連続力学系
1.2 離散力学系
1.3 強制ファンデルポール方程式への応用
1.4 線形解析
1.5 パターン形成への応用
研究課題
第2章 力学構造
2.1 位相共役性
2.2 双曲性
2.3 多様体
2.4 極限集合
2.5 位相的等価性と構造安定性
研究課題
第3章 カオスの例と特徴
3.1 初期値鋭敏性
3.2 分岐
3.3 記号化
3.4 多様体と馬蹄
3.5 カオスを理解するための力学概念
研究課題
第4章 局所的分岐
4.1 分岐とは
4.2 1次元システムの分岐
4.3 中心多様体
4.4 高次元システムの分岐
4.5 ローレンツモデルへの応用
4.6 分岐の実例
研究課題
第5章 大域的分岐
5.1 サドル接続
5.2 2次元サドル分岐
5.3 3次元ホモクリニック分岐
5.4 興味深いいくつかの分岐
5.5 減衰強制ダッフィング振動子
5.6 ホモクリニック分岐の一般論
5.7 メルニコフの方法
研究課題
第6章 記号力学系
6.1 ヘテロクリニック分岐の特徴
6.2 スメールの馬蹄形写 像
6.3 記号列空間と記号力学系
6.4 双曲型不変集合上の記号力学系
研究課題
第7章 カオス
7.1 カオスとは
7.2 双曲型不変集合
7.3 構造安定性
7.4 セクターバンドル
7.5 エノン写像
研究課題
参考文献
索引