「ブラックホールと時空の方程式:15歳からの一般相対論:小林晋平」(電子版)
内容紹介:
物理学者は、いかにして現象を記述し、世界を見るのか?
「ブラックホールを数式で表す」とは、いったいどういうことなのか?
高校数学から出発し、「一般相対論」へと一気に駆け上がる、
本気の物理学を知るための独習書。
~15歳の読者へ~
本書では、15歳、つまり中学3年生~高校1年生くらいを想定して、「ブラックホールを表す数式を導くところまで一緒に歩いていく」ことを目指しました。本書に出てくる数式の意味や、そこに描かれている物理の世界を理解するための数学や物理学の知識はそのつど説明しています。とはいえ、本書の内容をすべて理解するのは難しいかもしれません。わからないところは飛ばしながら、挑んでみてください。
~高校で物理と数学を学んだことのある方へ~
高校で学んだ内容が、実は一般相対論という最高峰の物理理論に直結している様子を味わっていただければと思います。大学で学ぶ数学も出てきますが、物理を介することでそれらが具体的になり、実感をもちやすくなるはずです。
~すでに一般相対論を学んだ方へ~
一般相対論には多くのすぐれた入門書があります。それらの多くでは、歴史の時系列に沿って解説するスタイルが採用されています。本書はそれらとは少し異なり、「ブラックホールを表す数式を理解する」という目的を最初に置き、その目的を達成するために必要な道具を揃えていくという、理論物理学者が研究を進める際と同じスタイルをとります。直感的イメージを重要視し、目標に向かってなるべく短いルートで進むことを目指したこともあり、厳密な議論は割愛せざるを得なかったところもあります。詳細な議論は他の専門書で補いつつ、一般相対論のモチベーションに立ち返り、また新たな視点でそれをとらえるきっかけとしていただければと思います。
2018年12月12日刊行、288ページ。
著者について:
小林晋平(こばやし しんぺい): ホームページ:http://shimpei.sgtpepper.net/welcome.html
1974年長野県生まれ。東京学芸大学教育学部准教授。相対論、宇宙論、量子重力を専門とする理論物理学者。2004年、京都大学大学院人間・環境学研究科博士課程修了。博士(人間・環境学)。東京大学大学院理学系研究科附属ビッグバン宇宙国際研究センター研究員、日本学術会議海外特別研究員(カナダ・ウォータールー大学およびペリメーター理論物理学研究所にて研究)、群馬工業高等専門学校准教授を経て、2015年より現職。群馬高専では6年連続して学生からベストティーチャーに選出される。相対論・宇宙論・量子論をわかりやすく解説する一般向け講座を多数開催している。
理数系書籍のレビュー記事は本書で381冊目。
発売から10日ほどで重版となる人気ぶりである。今話題の本だから僕がわざわざ紹介するまでもないのかもしれない。タイトルの「15歳からの~」、「ブラックホール」、「時空の方程式」という3つのキーワードはかなり強烈だ。
僕がブルーバックスで相対性理論を知ったのは40年前の高校1年生のときだ。学校の勉強とはまったく違う物理学の世界をワクワクしながら読みふけっていたのだが、数式を使って研究された成果だという事実を軽視していた。本にはおそらくアインシュタイン方程式くらいは紹介されていたと思うのだが、意味不明の数式であったことは間違いない。
もしその頃に本書のような本がでていたら、僕はよろこんで飛びついたことだろう。当時の僕が読み通せていたかはわからない。もちろん今ならすらすら読めるわけだが、過去にさかのぼって自分の数式の理解力を判断するのは困難だ。だとしても、わからないところを残しながら読み進めていたのだろうなぁと想像している。
近年、相対性理論(特に一般相対性理論)を数式で理解させるための本のハードルは低くなっている。本書が刊行される前ならば、発売情報として書いた「一般相対性理論を一歩一歩数式で理解する: 石井俊全」が代表例で、この記事の中に他の本との比較を書いたことがある。また「一般相対性理論に挑戦しよう!」という記事では、ゴールに到達するための最短ルートを紹介しておいた。しかし、これらはすべて高校卒業程度の数学と物理学の知識があることを前提としている。
今回発売された「ブラックホールと時空の方程式:15歳からの一般相対論:小林晋平」は、前提知識のスタートラインをさらに3歳下げて「中学卒業程度の数学と理科の知識」に設定したことである。そしてたかだか288ページの1冊の本として完結しているのが重要な点だ。
相対性理論の本をいくつも読み込んでいる僕でさえ「え、そんなことが可能なの?」と思うわけだ。高校数学と物理の部分は学習参考書や教科書で学べばよいじゃないか?そのように思ってしまう。出発点はやはり高校卒業程度にしておくのがいいんじゃないかな?そのような固定観念を持ちながら本書を読んでみたのだ。著者の小林先生は既刊の本を意識されていたはずで、結果的に既刊本との棲み分けに成功し、「競合」しない本に仕上がっている。
本書の章立てと構成はこのとおり。
第1章 ブラックホールを「表す」:数式から現れる世界
第2章 距離を測る:線素と微分積分
第3章 測り方を変えてみる:デカルト座標から極座標へ
第4章 次元を上げる:偏微分と3次元極座標
第5章 「時間と空間」から「時空」へ:特殊相対論
第6章 空間の曲がりを表現する:ベクトルと曲率
第7章 重力は時空の曲がりである:一般相対論
第8章 ブラックホール解を導く:アインシュタイン方程式とシュヴァルツシルト解
付録A 特殊相対論に関する補足
付録B 一般相対論に関する補足
付録C よく使う微分積分の公式
拡大
![]()
高校1年生に戻った自分を想像して読み始めてみた。しかし、これまでに一般相対性理論の教科書は何冊も読んでいるからシミュレーションにはやはり無理があるようで、すらすらと読み進んでしまう。こんなに丁寧に書かれているのにハイペースで読むから「あー、もったいない!」と、少々悔しい思いがした。ゴールにたどり着くまでに学ぶべき数学は、図版を多用しながら、そして高校では学ばない物理を取り入れ、興味を掻き立てるように書かれていた。次のような数学が学べるわけである。
高校数学の範囲:
- ピタゴラスの定理
- 微積分
- 三角比、三角関数
- デカルト座標と極座標、そしてその変換
- ベクトルと行列
大学数学の範囲:
- 偏微分
- テンソル
- 微分幾何学、リーマン幾何学(ベクトル場、共変微分、曲率、内在幾何、計量、接続、測地線)
これらの数学を前提知識として他の本で学ぶとしたら、高校1年生にはおそらく無理なわけで、「1冊で完結している」という本書の特長が効いてくるわけだ。さらにガリレイの相対性原理やニュートン力学も数学を学びながら自然に理解することができる。
本書で学ぶ物理学的内容は詳細目次を参考にしていただきたいが、第5章で特殊相対論やミンコフスキー時空にたどり着くことができる。(特殊相対論で導かれる有名な「E=mc²」は付録A「特殊相対論に関する補足」で導出されている。(「EMANの相対性理論」での「E=mc² の求め方」)
そして第7章で一般相対論が解説され、第8章の冒頭でアインシュタイン方程式が紹介されている。相対性理論の本質が「4次元時空の幾何学」であることから、本書全体で幾何学の記述が多くなるのは当然であるが、アインシュタイン方程式自体の解説は第7章に文章で説明しているだけなので、右辺のテンソル「T」の中身の数式的な解説が少々物足りなく感じた。(ページ数が限られているから仕方がないのかもしれない。)
アインシュタイン方程式(左辺は時空の曲がり具合、右辺は物質の分布)
![]()
本書は時空の幾何(左辺)の解説に重点が置かれている。右辺の「T」、つまり物質の分布の部分については「エネルギー運動量テンソル」を参考になさるとよい。
第8章では冒頭でアインシュタイン方程式を紹介し、それをブラックホールに適用し、もっとも基本的、代表的な「シュヴァルツシルト解」の導出が行われている。ブラックホールの表面を通過するとき、どのようなことが起こるのか?ブラックホールの中や中心はどうなっているのか?などは素人でも興味を掻き立てられるテーマである。一般相対性理論だけでは解明できないこのテーマは宇宙誕生の謎の解明に直結していて、どのようにこの壮大なテーマの研究が始まったのかを理解することができる。
ページ数を抑えたため、一般相対性理論から導かれる「重力波」や「水星の近日点移動」、「重力レンズ効果」、「天体の回転よる時空の引きずり効果」などは省略されている。それらは本書を読み終えた後、巻末の参考文献で紹介されているような本で学べばよいと思う。
読み終えた後にまず思ったのは、ごまかすことなく丁寧さを保ちながら、よくこのページ数で書き上げられているなぁということだ。「15歳からの~」は確かにキャッチコピーとしてはわかるが、言い過ぎかもしれない。世の中の平均的な15歳のうち何割くらいが本書を読破、理解できるのだろうか?
僕が想像するおよその感触は次のとおりである。
- 全国の高校1年生のうち完読できる人は1%くらい。
- 将来理系の大学に進むことになる高校1年生のうち完読できる人は5%くらい。
- 将来大学で物理学科に進むことになる高校1年生のうち完読できる人は10%くらい。
- 将来東大、京大、大阪大学などの物理学科に進むことになる高校1年生のうち完読できる人は20%くらい。
- 灘高校、開成高校の理系の高校1年生のうち完読できる人は40%くらい。
- 将来物理学の分野で博士号を取得することになる高校1年生のうち完読できる人は70%くらい。
- 数学オリンピックに出場経験のある高校1年生のうち完読できる人は90%くらい。
- 将来ノーベル物理学賞を受賞することになる高校1年生のうち完読できる人は100%。
本書を手に取ったことがきっかけで、数十年後にノーベル物理学賞を受賞する子供が出ればよいなぁと楽しい空想に浸った読書体験となった。中学までは数学できたのにと思っている方は、ぜひ書店で立ち読みをしてみてほしい。
本書に寄せた森田先生、橋本先生の推薦文は以下のとおり。
「たった一行の方程式を理解する経験が、どれほど豊かなことかを著者は教えてくれる。物理と、物理を学ぼうとするすべての人への思いが詰まった、まるで個人授業を受けているかのようなライブ感溢れるテキスト。」
――森田真生(独立研究者、『数学する身体』著者)
「ブラックホール時空への直通の登頂路!
シュバルツシルト解をじっくり「鑑賞」することから始まる本書は、そこに三平方の定理が隠されていることを見つけ、時空の冒険が始まる。平らな空間とは何か、座標とは何か、時間と空間、といった、ブラックホール解を理解する最小要素がかみ砕かれて解説される。丹念にその文章と数式を追っていくと、最後にはアインシュタイン方程式とシュバルツシルト解、という山に登頂させてくれるのだ。
初学者が詰まりがちなポイントも丁寧に説明され、痒いところに手が届いている。空間や距離の考え方の解説に前半が費やされているので、自分のペースでじっくり登ることができるため、高校生に登山道を開いてくれている。友人や、物理や数学の先生と一緒に登れば、なお楽しい登山になるに違いない。著者の「物理学者」感もにじみ出て、一緒に山に登ってくれる好著。」
――橋本幸士(物理学者、『「宇宙のすべてを支配する数式」をパパに習ってみた』著者)
関連記事:
一般相対性理論に挑戦しよう!
https://blog.goo.ne.jp/ktonegaw/e/ea7ad9292ce01ad4abbbc8c98f3303d0
発売情報:一般相対性理論を一歩一歩数式で理解する: 石井俊全
https://blog.goo.ne.jp/ktonegaw/e/1699a1c22477c269c68c02091d0ca049
趣味で物理学:広江克彦
https://blog.goo.ne.jp/ktonegaw/e/90aa60383b600ff4e4fd7bea6589deaa
趣味で相対論:広江克彦
https://blog.goo.ne.jp/ktonegaw/e/90aa60383b600ff4e4fd7bea6589deaa
時空の幾何学:特殊および一般相対論の数学的基礎
https://blog.goo.ne.jp/ktonegaw/e/ffc643a688ce45dec7460d107fe1392e
重力(上) アインシュタインの一般相対性理論入門: ジェームズ・B・ハートル
https://blog.goo.ne.jp/ktonegaw/e/d45a93d43478a133c6a514c980572632
重力(下) アインシュタインの一般相対性理論入門: ジェームズ・B・ハートル
https://blog.goo.ne.jp/ktonegaw/e/ae6e91eec0ecb404b3b77d46ca04b49b
重力理論 Gravitation-古典力学から相対性理論まで、時空の幾何学から宇宙の構造へ
https://blog.goo.ne.jp/ktonegaw/e/f838b8f6c2554000933187df89e08013
日本物理学会2016年度公開講座 「一般相対性理論と宇宙 -重力波研究の最前線-」
https://blog.goo.ne.jp/ktonegaw/e/d39ec747fb47e0c8418e7e167e2f60c4
マックスウェル方程式を1本にまとめたのは誰?
https://blog.goo.ne.jp/ktonegaw/e/226568b2c27822fb9fdfdb088e7018d3
マーミン相対論―新しい発想で学ぶ: デヴィッド マーミン
https://blog.goo.ne.jp/ktonegaw/e/6e47253b0622e867f57fb15b88d18149
1つずつ応援クリックをお願いします。
![にほんブログ村 科学ブログ 物理学へ]()
![人気ブログランキングへ]()
![]()
![]()
![]()
![]()
![]()
「ブラックホールと時空の方程式:15歳からの一般相対論:小林晋平」(電子版)
![]()
はじめに
第1章 ブラックホールを「表す」:数式から現れる世界
1.1 ブラックホールとは?
1.2 ブラックホール時空を数式で表す
1.3 数式から読み取れる物理
1.4 本書の構成
第2章 距離を測る:線素と微分積分
2.1 三平方の定理
2.2 局所的に考える・瞬間的に考える
2.3 微分積分の考え方
2.4 力学は微分積分の式で書かれる
第3章 測り方を変えてみる:デカルト座標から極座標へ
3.1 座標はなぜ必要か
3.2 デカルト座標と極座標
3.3 三角比とは
3.4 デカルト座標と極座標の関係:三角比の応用と座標変換
3.5 極座標での線素
3.6 時空の三平方の定理を表す量:計量
第4章 次元を上げる:偏微分と3次元極座標
4.1 3次元空間とデカルト座標
4.2 偏微分と全微分
4.3 線素の使い道:球面上の距離
第5章 「時間と空間」から「時空」へ:特殊相対論
5.1 光速の謎:物理法則と不変性の関係
5.2 特殊相対論における速度の加法則
5.3 時空の新しい見方:光速の不変性とローレンツ変換
5.4 特殊相対論の式をすっきりと表すために:行列
5.5 線素から世界間隔へ
5.6 科学には適用範囲がある
第6章 空間の曲がりを表現する:ベクトルと曲率
6.1 一般座標変換とベクトル・テンソル
6.2 ベクトルと曲率
6.3 ベクトルを微分する:偏微分と共変微分
6.4 接続と計量の関係
6.5 接続から曲率へ
6.6 曲率の具体的な計算
6.7 内在的曲率と外在的曲率
第7章 重力は時空の曲がりである:一般相対論
7.1 特殊相対論から一般相対論へ
7.2 一般相対論の基本原理
7.3 曲がった時空と重力の類似性
7.4 「重力=時空の曲がり」と数式
第8章 ブラックホール解を導く:アインシュタイン方程式とシュヴァルツシルト解
8.1 アインシュタイン方程式
8.2 シュヴァルツシルト解を求める
8.3 シュヴァルツシルト解を読み解く
おわりに
付録A 特殊相対論に関する補足
A.1 ローレンツ変換の導出
A.2 速度の合成則の導出
A.3 運動物体における時間の遅れとローレンツ収縮
A.4 固有時間と物理量の4次元化
付録B 一般相対論に関する補足
B.1 テンソルと変換性について
B.2 滑らかな空間と局所的に平坦な空間について
B.3 測地線と測地線方程式
B.4 シュヴァルツシルト解における積分定数の決定
B.5 パンルヴェグルストランド座標について
付録C よく使う微分積分の公式
参考文献
索引
内容紹介:
物理学者は、いかにして現象を記述し、世界を見るのか?
「ブラックホールを数式で表す」とは、いったいどういうことなのか?
高校数学から出発し、「一般相対論」へと一気に駆け上がる、
本気の物理学を知るための独習書。
~15歳の読者へ~
本書では、15歳、つまり中学3年生~高校1年生くらいを想定して、「ブラックホールを表す数式を導くところまで一緒に歩いていく」ことを目指しました。本書に出てくる数式の意味や、そこに描かれている物理の世界を理解するための数学や物理学の知識はそのつど説明しています。とはいえ、本書の内容をすべて理解するのは難しいかもしれません。わからないところは飛ばしながら、挑んでみてください。
~高校で物理と数学を学んだことのある方へ~
高校で学んだ内容が、実は一般相対論という最高峰の物理理論に直結している様子を味わっていただければと思います。大学で学ぶ数学も出てきますが、物理を介することでそれらが具体的になり、実感をもちやすくなるはずです。
~すでに一般相対論を学んだ方へ~
一般相対論には多くのすぐれた入門書があります。それらの多くでは、歴史の時系列に沿って解説するスタイルが採用されています。本書はそれらとは少し異なり、「ブラックホールを表す数式を理解する」という目的を最初に置き、その目的を達成するために必要な道具を揃えていくという、理論物理学者が研究を進める際と同じスタイルをとります。直感的イメージを重要視し、目標に向かってなるべく短いルートで進むことを目指したこともあり、厳密な議論は割愛せざるを得なかったところもあります。詳細な議論は他の専門書で補いつつ、一般相対論のモチベーションに立ち返り、また新たな視点でそれをとらえるきっかけとしていただければと思います。
2018年12月12日刊行、288ページ。
著者について:
小林晋平(こばやし しんぺい): ホームページ:http://shimpei.sgtpepper.net/welcome.html
1974年長野県生まれ。東京学芸大学教育学部准教授。相対論、宇宙論、量子重力を専門とする理論物理学者。2004年、京都大学大学院人間・環境学研究科博士課程修了。博士(人間・環境学)。東京大学大学院理学系研究科附属ビッグバン宇宙国際研究センター研究員、日本学術会議海外特別研究員(カナダ・ウォータールー大学およびペリメーター理論物理学研究所にて研究)、群馬工業高等専門学校准教授を経て、2015年より現職。群馬高専では6年連続して学生からベストティーチャーに選出される。相対論・宇宙論・量子論をわかりやすく解説する一般向け講座を多数開催している。
理数系書籍のレビュー記事は本書で381冊目。
発売から10日ほどで重版となる人気ぶりである。今話題の本だから僕がわざわざ紹介するまでもないのかもしれない。タイトルの「15歳からの~」、「ブラックホール」、「時空の方程式」という3つのキーワードはかなり強烈だ。
僕がブルーバックスで相対性理論を知ったのは40年前の高校1年生のときだ。学校の勉強とはまったく違う物理学の世界をワクワクしながら読みふけっていたのだが、数式を使って研究された成果だという事実を軽視していた。本にはおそらくアインシュタイン方程式くらいは紹介されていたと思うのだが、意味不明の数式であったことは間違いない。
もしその頃に本書のような本がでていたら、僕はよろこんで飛びついたことだろう。当時の僕が読み通せていたかはわからない。もちろん今ならすらすら読めるわけだが、過去にさかのぼって自分の数式の理解力を判断するのは困難だ。だとしても、わからないところを残しながら読み進めていたのだろうなぁと想像している。
近年、相対性理論(特に一般相対性理論)を数式で理解させるための本のハードルは低くなっている。本書が刊行される前ならば、発売情報として書いた「一般相対性理論を一歩一歩数式で理解する: 石井俊全」が代表例で、この記事の中に他の本との比較を書いたことがある。また「一般相対性理論に挑戦しよう!」という記事では、ゴールに到達するための最短ルートを紹介しておいた。しかし、これらはすべて高校卒業程度の数学と物理学の知識があることを前提としている。
今回発売された「ブラックホールと時空の方程式:15歳からの一般相対論:小林晋平」は、前提知識のスタートラインをさらに3歳下げて「中学卒業程度の数学と理科の知識」に設定したことである。そしてたかだか288ページの1冊の本として完結しているのが重要な点だ。
相対性理論の本をいくつも読み込んでいる僕でさえ「え、そんなことが可能なの?」と思うわけだ。高校数学と物理の部分は学習参考書や教科書で学べばよいじゃないか?そのように思ってしまう。出発点はやはり高校卒業程度にしておくのがいいんじゃないかな?そのような固定観念を持ちながら本書を読んでみたのだ。著者の小林先生は既刊の本を意識されていたはずで、結果的に既刊本との棲み分けに成功し、「競合」しない本に仕上がっている。
本書の章立てと構成はこのとおり。
第1章 ブラックホールを「表す」:数式から現れる世界
第2章 距離を測る:線素と微分積分
第3章 測り方を変えてみる:デカルト座標から極座標へ
第4章 次元を上げる:偏微分と3次元極座標
第5章 「時間と空間」から「時空」へ:特殊相対論
第6章 空間の曲がりを表現する:ベクトルと曲率
第7章 重力は時空の曲がりである:一般相対論
第8章 ブラックホール解を導く:アインシュタイン方程式とシュヴァルツシルト解
付録A 特殊相対論に関する補足
付録B 一般相対論に関する補足
付録C よく使う微分積分の公式
拡大

高校1年生に戻った自分を想像して読み始めてみた。しかし、これまでに一般相対性理論の教科書は何冊も読んでいるからシミュレーションにはやはり無理があるようで、すらすらと読み進んでしまう。こんなに丁寧に書かれているのにハイペースで読むから「あー、もったいない!」と、少々悔しい思いがした。ゴールにたどり着くまでに学ぶべき数学は、図版を多用しながら、そして高校では学ばない物理を取り入れ、興味を掻き立てるように書かれていた。次のような数学が学べるわけである。
高校数学の範囲:
- ピタゴラスの定理
- 微積分
- 三角比、三角関数
- デカルト座標と極座標、そしてその変換
- ベクトルと行列
大学数学の範囲:
- 偏微分
- テンソル
- 微分幾何学、リーマン幾何学(ベクトル場、共変微分、曲率、内在幾何、計量、接続、測地線)
これらの数学を前提知識として他の本で学ぶとしたら、高校1年生にはおそらく無理なわけで、「1冊で完結している」という本書の特長が効いてくるわけだ。さらにガリレイの相対性原理やニュートン力学も数学を学びながら自然に理解することができる。
本書で学ぶ物理学的内容は詳細目次を参考にしていただきたいが、第5章で特殊相対論やミンコフスキー時空にたどり着くことができる。(特殊相対論で導かれる有名な「E=mc²」は付録A「特殊相対論に関する補足」で導出されている。(「EMANの相対性理論」での「E=mc² の求め方」)
そして第7章で一般相対論が解説され、第8章の冒頭でアインシュタイン方程式が紹介されている。相対性理論の本質が「4次元時空の幾何学」であることから、本書全体で幾何学の記述が多くなるのは当然であるが、アインシュタイン方程式自体の解説は第7章に文章で説明しているだけなので、右辺のテンソル「T」の中身の数式的な解説が少々物足りなく感じた。(ページ数が限られているから仕方がないのかもしれない。)
アインシュタイン方程式(左辺は時空の曲がり具合、右辺は物質の分布)
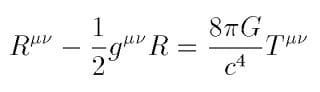
本書は時空の幾何(左辺)の解説に重点が置かれている。右辺の「T」、つまり物質の分布の部分については「エネルギー運動量テンソル」を参考になさるとよい。
第8章では冒頭でアインシュタイン方程式を紹介し、それをブラックホールに適用し、もっとも基本的、代表的な「シュヴァルツシルト解」の導出が行われている。ブラックホールの表面を通過するとき、どのようなことが起こるのか?ブラックホールの中や中心はどうなっているのか?などは素人でも興味を掻き立てられるテーマである。一般相対性理論だけでは解明できないこのテーマは宇宙誕生の謎の解明に直結していて、どのようにこの壮大なテーマの研究が始まったのかを理解することができる。
ページ数を抑えたため、一般相対性理論から導かれる「重力波」や「水星の近日点移動」、「重力レンズ効果」、「天体の回転よる時空の引きずり効果」などは省略されている。それらは本書を読み終えた後、巻末の参考文献で紹介されているような本で学べばよいと思う。
読み終えた後にまず思ったのは、ごまかすことなく丁寧さを保ちながら、よくこのページ数で書き上げられているなぁということだ。「15歳からの~」は確かにキャッチコピーとしてはわかるが、言い過ぎかもしれない。世の中の平均的な15歳のうち何割くらいが本書を読破、理解できるのだろうか?
僕が想像するおよその感触は次のとおりである。
- 全国の高校1年生のうち完読できる人は1%くらい。
- 将来理系の大学に進むことになる高校1年生のうち完読できる人は5%くらい。
- 将来大学で物理学科に進むことになる高校1年生のうち完読できる人は10%くらい。
- 将来東大、京大、大阪大学などの物理学科に進むことになる高校1年生のうち完読できる人は20%くらい。
- 灘高校、開成高校の理系の高校1年生のうち完読できる人は40%くらい。
- 将来物理学の分野で博士号を取得することになる高校1年生のうち完読できる人は70%くらい。
- 数学オリンピックに出場経験のある高校1年生のうち完読できる人は90%くらい。
- 将来ノーベル物理学賞を受賞することになる高校1年生のうち完読できる人は100%。
本書を手に取ったことがきっかけで、数十年後にノーベル物理学賞を受賞する子供が出ればよいなぁと楽しい空想に浸った読書体験となった。中学までは数学できたのにと思っている方は、ぜひ書店で立ち読みをしてみてほしい。
本書に寄せた森田先生、橋本先生の推薦文は以下のとおり。
「たった一行の方程式を理解する経験が、どれほど豊かなことかを著者は教えてくれる。物理と、物理を学ぼうとするすべての人への思いが詰まった、まるで個人授業を受けているかのようなライブ感溢れるテキスト。」
――森田真生(独立研究者、『数学する身体』著者)
「ブラックホール時空への直通の登頂路!
シュバルツシルト解をじっくり「鑑賞」することから始まる本書は、そこに三平方の定理が隠されていることを見つけ、時空の冒険が始まる。平らな空間とは何か、座標とは何か、時間と空間、といった、ブラックホール解を理解する最小要素がかみ砕かれて解説される。丹念にその文章と数式を追っていくと、最後にはアインシュタイン方程式とシュバルツシルト解、という山に登頂させてくれるのだ。
初学者が詰まりがちなポイントも丁寧に説明され、痒いところに手が届いている。空間や距離の考え方の解説に前半が費やされているので、自分のペースでじっくり登ることができるため、高校生に登山道を開いてくれている。友人や、物理や数学の先生と一緒に登れば、なお楽しい登山になるに違いない。著者の「物理学者」感もにじみ出て、一緒に山に登ってくれる好著。」
――橋本幸士(物理学者、『「宇宙のすべてを支配する数式」をパパに習ってみた』著者)
関連記事:
一般相対性理論に挑戦しよう!
https://blog.goo.ne.jp/ktonegaw/e/ea7ad9292ce01ad4abbbc8c98f3303d0
発売情報:一般相対性理論を一歩一歩数式で理解する: 石井俊全
https://blog.goo.ne.jp/ktonegaw/e/1699a1c22477c269c68c02091d0ca049
趣味で物理学:広江克彦
https://blog.goo.ne.jp/ktonegaw/e/90aa60383b600ff4e4fd7bea6589deaa
趣味で相対論:広江克彦
https://blog.goo.ne.jp/ktonegaw/e/90aa60383b600ff4e4fd7bea6589deaa
時空の幾何学:特殊および一般相対論の数学的基礎
https://blog.goo.ne.jp/ktonegaw/e/ffc643a688ce45dec7460d107fe1392e
重力(上) アインシュタインの一般相対性理論入門: ジェームズ・B・ハートル
https://blog.goo.ne.jp/ktonegaw/e/d45a93d43478a133c6a514c980572632
重力(下) アインシュタインの一般相対性理論入門: ジェームズ・B・ハートル
https://blog.goo.ne.jp/ktonegaw/e/ae6e91eec0ecb404b3b77d46ca04b49b
重力理論 Gravitation-古典力学から相対性理論まで、時空の幾何学から宇宙の構造へ
https://blog.goo.ne.jp/ktonegaw/e/f838b8f6c2554000933187df89e08013
日本物理学会2016年度公開講座 「一般相対性理論と宇宙 -重力波研究の最前線-」
https://blog.goo.ne.jp/ktonegaw/e/d39ec747fb47e0c8418e7e167e2f60c4
マックスウェル方程式を1本にまとめたのは誰?
https://blog.goo.ne.jp/ktonegaw/e/226568b2c27822fb9fdfdb088e7018d3
マーミン相対論―新しい発想で学ぶ: デヴィッド マーミン
https://blog.goo.ne.jp/ktonegaw/e/6e47253b0622e867f57fb15b88d18149
1つずつ応援クリックをお願いします。







「ブラックホールと時空の方程式:15歳からの一般相対論:小林晋平」(電子版)

はじめに
第1章 ブラックホールを「表す」:数式から現れる世界
1.1 ブラックホールとは?
1.2 ブラックホール時空を数式で表す
1.3 数式から読み取れる物理
1.4 本書の構成
第2章 距離を測る:線素と微分積分
2.1 三平方の定理
2.2 局所的に考える・瞬間的に考える
2.3 微分積分の考え方
2.4 力学は微分積分の式で書かれる
第3章 測り方を変えてみる:デカルト座標から極座標へ
3.1 座標はなぜ必要か
3.2 デカルト座標と極座標
3.3 三角比とは
3.4 デカルト座標と極座標の関係:三角比の応用と座標変換
3.5 極座標での線素
3.6 時空の三平方の定理を表す量:計量
第4章 次元を上げる:偏微分と3次元極座標
4.1 3次元空間とデカルト座標
4.2 偏微分と全微分
4.3 線素の使い道:球面上の距離
第5章 「時間と空間」から「時空」へ:特殊相対論
5.1 光速の謎:物理法則と不変性の関係
5.2 特殊相対論における速度の加法則
5.3 時空の新しい見方:光速の不変性とローレンツ変換
5.4 特殊相対論の式をすっきりと表すために:行列
5.5 線素から世界間隔へ
5.6 科学には適用範囲がある
第6章 空間の曲がりを表現する:ベクトルと曲率
6.1 一般座標変換とベクトル・テンソル
6.2 ベクトルと曲率
6.3 ベクトルを微分する:偏微分と共変微分
6.4 接続と計量の関係
6.5 接続から曲率へ
6.6 曲率の具体的な計算
6.7 内在的曲率と外在的曲率
第7章 重力は時空の曲がりである:一般相対論
7.1 特殊相対論から一般相対論へ
7.2 一般相対論の基本原理
7.3 曲がった時空と重力の類似性
7.4 「重力=時空の曲がり」と数式
第8章 ブラックホール解を導く:アインシュタイン方程式とシュヴァルツシルト解
8.1 アインシュタイン方程式
8.2 シュヴァルツシルト解を求める
8.3 シュヴァルツシルト解を読み解く
おわりに
付録A 特殊相対論に関する補足
A.1 ローレンツ変換の導出
A.2 速度の合成則の導出
A.3 運動物体における時間の遅れとローレンツ収縮
A.4 固有時間と物理量の4次元化
付録B 一般相対論に関する補足
B.1 テンソルと変換性について
B.2 滑らかな空間と局所的に平坦な空間について
B.3 測地線と測地線方程式
B.4 シュヴァルツシルト解における積分定数の決定
B.5 パンルヴェグルストランド座標について
付録C よく使う微分積分の公式
参考文献
索引