「NHKスペシャル 100年の難問はなぜ解けたのか 天才数学者の光と影 : 春日真人」(Kindle版)(文庫版)
内容紹介:
ついに「ポアンカレ予想」が解決した!ところが…。世紀の難問に挑み、敗れ去った幾多の数学者と見事に解決したにもかかわらず姿を消した天才グリゴリ・ペレリマン。数学という魔物がもたらす数奇な運命とは―。
2008年6月刊行、229ページ。
著者について:
春日真人(かすがまさひと)
1968年生まれ、東京大学理学系研究科相関理化学修了、93年NHK入局。長野放送局、番組制作局教養番組部、番組開発を経て、現在、経済・社会情報番組ディレクター。ドキュメントにっぽん「いのち再び 生命科学者・柳澤桂子」、NHKスペシャル「親を知りたい」「中絶胎児利用の衝撃」「論文捏造 夢の医療はなぜ潰えたのか」など、先端医療や生命倫理をおもなフィールドとしてドキュメンタリー番組を制作。
春日さんの著書: Amazonで検索
理数系書籍のレビュー記事は本書で370冊目。
2003年に証明された「ポアンカレ予想」は2007年に放送された「ハイビジョン特集 数学者はキノコ狩りの夢を見る ~ポアンカレ予想・100年の格闘~」や「NHKスペシャル 100年の難問はなぜ解けたのか ~天才数学者 失踪(しっそう)の謎~」がきっかけとなり、ポアンカレ予想は一般の人に広く知られるようになった。
ポアンカレ予想関連の本の紹介を続けてきたが、本書を紹介してひとまずしめくくろう。番組を制作したディレクターが放送終了後に書籍化したのがこの本だ。刊行されてからちょうど10年たっている。
一般読者を対象としているだけに読みやすい。理系でない方にもお勧めできる本だ。章立ては次のとおり。
プロローグ 世紀の難問と謎の数学者
第1章 ペレリマン博士を追って
第2章 「ポアンカレ予想」の誕生
第3章 古典数学VSトポロジー
第4章 1950年代―「白鯨」に食われた数学者たち
第5章 1960年代―クラシックを捨てよ、ロックを聴こう
第6章 1980年代―天才サーストンの光と影
第7章 1990年代―開かれた解決への扉
エピローグ 終わりなき挑戦
科学教養書をもとにテレビ番組を作ると、たった10ページぶんを伝えるために1時間枠が必要になると言われている。そうだとすると本書には番組で伝えられなかったことがたくさんあるのだろうか?そのような期待をもたせてくれる。
結果から言うと違っていた。番組で伝えていた内容は本書では半分ほどを占めていた。後になって思えばこの番組の脚本のような本なのだと思う。残りの半分は番組では紹介しきれなかった内容だ。番組を見た人でも本書を読む価値はじゅうぶんある。
本のほうでは、ポアンカレ予想の意味を詳しく理解できること、ペレルマン以前にこの難問に挑んだ数学者たちの人生を知ることができる。
特にテレビ番組では誤解されがちだった「次元」に関する解説が本では正確にされているのがよい。つまり、番組ではまず「地球の形」を取り上げて、このような2つの絵を見せていた。
球面の場合(2次元の球面)
![]()
ドーナツ型(トーラス)の曲面の場合(2次元のトーラスの曲面)
![]()
この2つの例は2次元の曲面の形を取り上げているわけだが、番組では「2次元」という重要なキーワードを省略していた。
そして番組では次に「宇宙の形」を2つ例示するわけである。
3次元の曲面(3次元球面に同相)
![]()
3次元ドーナツ型の曲面(3次元トーラスの曲面)
![]()
地球の形と宇宙の形で同じような絵を使って説明しているから、視聴者は宇宙の形のほうで、ひとつ次元が上がっていることに気がきにくくなっている。地球の形のほうで赤いロープは曲面に沿って描かれているのに対し、宇宙の形では宇宙空間の中を通るように描かれている。描き方の微妙な違いに気がついた読者はほとんどいないだろう。
ポアンカレ予想はこの3次元の曲面についての予想なのである。本書では次元が上がった世界の話であることを、一般の読者に誤解を与えない表現で上手に解説している。
ポアンカレ予想とは「単連結な3次元閉多様体は3次元球面と同相と言えるか?」なのだ。
![]()
ポアンカレ予想の証明のカギとなった「サーストンの幾何化予想」の詳しいことは「低次元の幾何からポアンカレ予想へ : 市原一裕」で学ぶことができるが、理系分野にうとい読者には無理である。本書では番組で伝えきれなかった説明を一般の読者にも理解できるレベルで解説している。
サーストンの幾何化予想(基本となる3次元多様体の8つの断片)
![]()
昨年「宇宙の形、ガウスの曲面論と内在幾何(第3回)」という記事で、宇宙が平坦(曲がっていない)であることが宇宙マイクロ波背景放射の観測によって確認されたと述べた。曲がった宇宙を考えることに、もはや意味がなくなったのではないかと思った方がいるかもしれない。
でもそれは違う。平坦性が確認されたのは、たかだか半径137億光年の「狭い範囲」だけのことであり、その先の広大な宇宙の形が曲がっていたり穴が開いていたりする可能性は排除できないのだ。さらに言えば宇宙はサーストンの幾何化予想で示されている8つの形のうちのひとつかもしれない。本書ではそのことについても解説を与えている。
なぜポアンカレ予想が100年の難問だったのか?なぜペレルマンの証明がフィールズ賞を獲得したのか(そして受賞辞退されたのか)を、ドラマチックに堪能できる本である。NHKオンデマンドでもう一度番組をご覧になり、本書と比べるのもひとつの楽しみ方だ。
ポアンカレ予想を証明したペレルマンが2002年と2003年に「リッチフローの三次元多様体への応用」として掲載した論文は一般公開されている。以下のアドレスをクリックするとPDFで読むことができる。(理解しろという意味で紹介したわけではない。)
http://arxiv.org/find/all/1/au:+Perelman_Grisha/0/1/0/all/0/1
ペレルマンによる論文ではないが「リッチフローによるポアンカレ予想と幾何化予想の完全な証明」も以下のPDFファイルで読める。(こちらは328ページもある)
http://www.ims.cuhk.edu.hk/~ajm/vol10/10_2.pdf
あわせて読みたい:
一般向けの本では本書がいちばんよいと思うが、この他にもいくつか刊行されている。ここをクリックして検索してみるとよいだろう。
一般向けの本だが難解なのがこちら。理解しきれなくても難解な現代数学の世界のイメージがつかめる本だと思う。
「低次元の幾何からポアンカレ予想へ : 市原一裕」(Kindle版)(紹介記事)
![]()
巻頭 ポアンカレ予想に関わる図形たち
はじめに
第1章 ポアンカレ予想
第2章 多様体の幾何構造
第3章 サーストンの幾何化予想
第4章 ペレルマンの証明
付 録 非ユークリッド幾何について
読書案内
あとがき
専門書ではあるが、このような本のPDFファイルが無料で公開されている。(紹介記事)
「3次元多様体入門(培風館) : 森元勘治」
![]()
専門書だと、あとこの2冊が良さそうだ。
「3次元リッチフローと幾何学的トポロジー: 戸田正人」
「リッチフローと幾何化予想:小林亮一」(書評)(他の購入先)
![]()
![]()
関連記事:
数学ガール/ポアンカレ予想 : 結城浩
https://blog.goo.ne.jp/ktonegaw/e/769e2639898b351545e7ad8a8eba89d7
トポロジカル宇宙(完全版):根上生也著
https://blog.goo.ne.jp/ktonegaw/e/246a5c64c600c9c12c303231173ee9e2
無料公開:3次元多様体入門(培風館): 森元勘治
https://blog.goo.ne.jp/ktonegaw/e/7f5737d01d69c60f6320e28c049bc0f1
低次元の幾何からポアンカレ予想へ : 市原一裕
https://blog.goo.ne.jp/ktonegaw/e/4213d848aac806d19dfce9ae8202ab21
ブログ執筆のはげみになりますので、1つずつ応援クリックをお願いします。
![にほんブログ村 科学ブログ 物理学へ]()
![人気ブログランキングへ]()
![]()
![]()
![]()
![]()
![]()
「NHKスペシャル 100年の難問はなぜ解けたのか 天才数学者の光と影 : 春日真人」(Kindle版)(文庫版)
![]()
プロローグ 世紀の難問と謎の数学者
第1章 ペレリマン博士を追って
- 生まれ故郷サンクトペテルブルク
- 金も地位もいらない
- 変わり果てた天才少年
第2章 「ポアンカレ予想」の誕生
- 自由な数学を愛した天才ポアンカレ
- 「形」の謎に迫るポアンカレ予想
- まずは「地球の形」から
- 宇宙の形を調べる方法
第3章 古典数学VSトポロジー
- 数学のアール・ヌーヴォー
- トポロジーの魔法
- 「ポアンカレ予想」という悪夢
第4章 1950年代―「白鯨」に食われた数学者たち
- ギリシャからやってきた修行僧
- ドイツからの若きライバル
- ライバルたちの静かな闘い
- ある老数学者の述懐
第5章 1960年代―クラシックを捨てよ、ロックを聴こう
- 時代を席捲した「数学の王者」トポロジー
- ポアンカレ予想への奇襲作戦~スティーブン・スメール
- 「高次元」への旅が始まった
- 天才少年誕生
- 天才数学者の素顔
- トポロジーは死んだ?
第6章 1980年代―天才サーストンの光と影
- マジシャン登場
- 宇宙は本当に丸いのか~リンゴと葉っぱのマジック~
- 衝撃の新予想~宇宙の形は八つ?~
- 天才サーストンの苦悩
第7章 1990年代―開かれた解決への扉
- ロシアとアメリカの出会い
- 知られざる「転機」
- 七つの未解決問題
- 100年に一度の奇跡
- 世紀の難問が解けた
- なぜ彼だったのか
エピローグ 終わりなき挑戦
あとがき
内容紹介:
ついに「ポアンカレ予想」が解決した!ところが…。世紀の難問に挑み、敗れ去った幾多の数学者と見事に解決したにもかかわらず姿を消した天才グリゴリ・ペレリマン。数学という魔物がもたらす数奇な運命とは―。
2008年6月刊行、229ページ。
著者について:
春日真人(かすがまさひと)
1968年生まれ、東京大学理学系研究科相関理化学修了、93年NHK入局。長野放送局、番組制作局教養番組部、番組開発を経て、現在、経済・社会情報番組ディレクター。ドキュメントにっぽん「いのち再び 生命科学者・柳澤桂子」、NHKスペシャル「親を知りたい」「中絶胎児利用の衝撃」「論文捏造 夢の医療はなぜ潰えたのか」など、先端医療や生命倫理をおもなフィールドとしてドキュメンタリー番組を制作。
春日さんの著書: Amazonで検索
理数系書籍のレビュー記事は本書で370冊目。
2003年に証明された「ポアンカレ予想」は2007年に放送された「ハイビジョン特集 数学者はキノコ狩りの夢を見る ~ポアンカレ予想・100年の格闘~」や「NHKスペシャル 100年の難問はなぜ解けたのか ~天才数学者 失踪(しっそう)の謎~」がきっかけとなり、ポアンカレ予想は一般の人に広く知られるようになった。
ポアンカレ予想関連の本の紹介を続けてきたが、本書を紹介してひとまずしめくくろう。番組を制作したディレクターが放送終了後に書籍化したのがこの本だ。刊行されてからちょうど10年たっている。
一般読者を対象としているだけに読みやすい。理系でない方にもお勧めできる本だ。章立ては次のとおり。
プロローグ 世紀の難問と謎の数学者
第1章 ペレリマン博士を追って
第2章 「ポアンカレ予想」の誕生
第3章 古典数学VSトポロジー
第4章 1950年代―「白鯨」に食われた数学者たち
第5章 1960年代―クラシックを捨てよ、ロックを聴こう
第6章 1980年代―天才サーストンの光と影
第7章 1990年代―開かれた解決への扉
エピローグ 終わりなき挑戦
科学教養書をもとにテレビ番組を作ると、たった10ページぶんを伝えるために1時間枠が必要になると言われている。そうだとすると本書には番組で伝えられなかったことがたくさんあるのだろうか?そのような期待をもたせてくれる。
結果から言うと違っていた。番組で伝えていた内容は本書では半分ほどを占めていた。後になって思えばこの番組の脚本のような本なのだと思う。残りの半分は番組では紹介しきれなかった内容だ。番組を見た人でも本書を読む価値はじゅうぶんある。
本のほうでは、ポアンカレ予想の意味を詳しく理解できること、ペレルマン以前にこの難問に挑んだ数学者たちの人生を知ることができる。
特にテレビ番組では誤解されがちだった「次元」に関する解説が本では正確にされているのがよい。つまり、番組ではまず「地球の形」を取り上げて、このような2つの絵を見せていた。
球面の場合(2次元の球面)
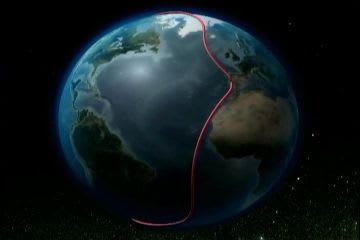
ドーナツ型(トーラス)の曲面の場合(2次元のトーラスの曲面)
この2つの例は2次元の曲面の形を取り上げているわけだが、番組では「2次元」という重要なキーワードを省略していた。
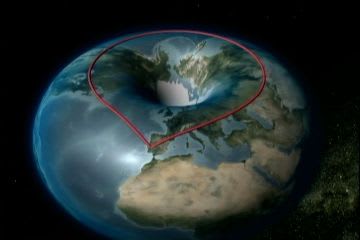
そして番組では次に「宇宙の形」を2つ例示するわけである。
3次元の曲面(3次元球面に同相)

3次元ドーナツ型の曲面(3次元トーラスの曲面)

地球の形と宇宙の形で同じような絵を使って説明しているから、視聴者は宇宙の形のほうで、ひとつ次元が上がっていることに気がきにくくなっている。地球の形のほうで赤いロープは曲面に沿って描かれているのに対し、宇宙の形では宇宙空間の中を通るように描かれている。描き方の微妙な違いに気がついた読者はほとんどいないだろう。
ポアンカレ予想はこの3次元の曲面についての予想なのである。本書では次元が上がった世界の話であることを、一般の読者に誤解を与えない表現で上手に解説している。
ポアンカレ予想とは「単連結な3次元閉多様体は3次元球面と同相と言えるか?」なのだ。

ポアンカレ予想の証明のカギとなった「サーストンの幾何化予想」の詳しいことは「低次元の幾何からポアンカレ予想へ : 市原一裕」で学ぶことができるが、理系分野にうとい読者には無理である。本書では番組で伝えきれなかった説明を一般の読者にも理解できるレベルで解説している。
サーストンの幾何化予想(基本となる3次元多様体の8つの断片)
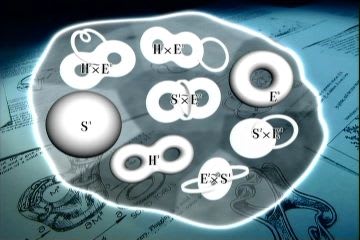
昨年「宇宙の形、ガウスの曲面論と内在幾何(第3回)」という記事で、宇宙が平坦(曲がっていない)であることが宇宙マイクロ波背景放射の観測によって確認されたと述べた。曲がった宇宙を考えることに、もはや意味がなくなったのではないかと思った方がいるかもしれない。
でもそれは違う。平坦性が確認されたのは、たかだか半径137億光年の「狭い範囲」だけのことであり、その先の広大な宇宙の形が曲がっていたり穴が開いていたりする可能性は排除できないのだ。さらに言えば宇宙はサーストンの幾何化予想で示されている8つの形のうちのひとつかもしれない。本書ではそのことについても解説を与えている。
なぜポアンカレ予想が100年の難問だったのか?なぜペレルマンの証明がフィールズ賞を獲得したのか(そして受賞辞退されたのか)を、ドラマチックに堪能できる本である。NHKオンデマンドでもう一度番組をご覧になり、本書と比べるのもひとつの楽しみ方だ。
ポアンカレ予想を証明したペレルマンが2002年と2003年に「リッチフローの三次元多様体への応用」として掲載した論文は一般公開されている。以下のアドレスをクリックするとPDFで読むことができる。(理解しろという意味で紹介したわけではない。)
http://arxiv.org/find/all/1/au:+Perelman_Grisha/0/1/0/all/0/1
ペレルマンによる論文ではないが「リッチフローによるポアンカレ予想と幾何化予想の完全な証明」も以下のPDFファイルで読める。(こちらは328ページもある)
http://www.ims.cuhk.edu.hk/~ajm/vol10/10_2.pdf
あわせて読みたい:
一般向けの本では本書がいちばんよいと思うが、この他にもいくつか刊行されている。ここをクリックして検索してみるとよいだろう。
一般向けの本だが難解なのがこちら。理解しきれなくても難解な現代数学の世界のイメージがつかめる本だと思う。
「低次元の幾何からポアンカレ予想へ : 市原一裕」(Kindle版)(紹介記事)

巻頭 ポアンカレ予想に関わる図形たち
はじめに
第1章 ポアンカレ予想
第2章 多様体の幾何構造
第3章 サーストンの幾何化予想
第4章 ペレルマンの証明
付 録 非ユークリッド幾何について
読書案内
あとがき
専門書ではあるが、このような本のPDFファイルが無料で公開されている。(紹介記事)
「3次元多様体入門(培風館) : 森元勘治」

専門書だと、あとこの2冊が良さそうだ。
「3次元リッチフローと幾何学的トポロジー: 戸田正人」
「リッチフローと幾何化予想:小林亮一」(書評)(他の購入先)


関連記事:
数学ガール/ポアンカレ予想 : 結城浩
https://blog.goo.ne.jp/ktonegaw/e/769e2639898b351545e7ad8a8eba89d7
トポロジカル宇宙(完全版):根上生也著
https://blog.goo.ne.jp/ktonegaw/e/246a5c64c600c9c12c303231173ee9e2
無料公開:3次元多様体入門(培風館): 森元勘治
https://blog.goo.ne.jp/ktonegaw/e/7f5737d01d69c60f6320e28c049bc0f1
低次元の幾何からポアンカレ予想へ : 市原一裕
https://blog.goo.ne.jp/ktonegaw/e/4213d848aac806d19dfce9ae8202ab21
ブログ執筆のはげみになりますので、1つずつ応援クリックをお願いします。







「NHKスペシャル 100年の難問はなぜ解けたのか 天才数学者の光と影 : 春日真人」(Kindle版)(文庫版)

プロローグ 世紀の難問と謎の数学者
第1章 ペレリマン博士を追って
- 生まれ故郷サンクトペテルブルク
- 金も地位もいらない
- 変わり果てた天才少年
第2章 「ポアンカレ予想」の誕生
- 自由な数学を愛した天才ポアンカレ
- 「形」の謎に迫るポアンカレ予想
- まずは「地球の形」から
- 宇宙の形を調べる方法
第3章 古典数学VSトポロジー
- 数学のアール・ヌーヴォー
- トポロジーの魔法
- 「ポアンカレ予想」という悪夢
第4章 1950年代―「白鯨」に食われた数学者たち
- ギリシャからやってきた修行僧
- ドイツからの若きライバル
- ライバルたちの静かな闘い
- ある老数学者の述懐
第5章 1960年代―クラシックを捨てよ、ロックを聴こう
- 時代を席捲した「数学の王者」トポロジー
- ポアンカレ予想への奇襲作戦~スティーブン・スメール
- 「高次元」への旅が始まった
- 天才少年誕生
- 天才数学者の素顔
- トポロジーは死んだ?
第6章 1980年代―天才サーストンの光と影
- マジシャン登場
- 宇宙は本当に丸いのか~リンゴと葉っぱのマジック~
- 衝撃の新予想~宇宙の形は八つ?~
- 天才サーストンの苦悩
第7章 1990年代―開かれた解決への扉
- ロシアとアメリカの出会い
- 知られざる「転機」
- 七つの未解決問題
- 100年に一度の奇跡
- 世紀の難問が解けた
- なぜ彼だったのか
エピローグ 終わりなき挑戦
あとがき