「
量子的世界像 101の新知識: ケネス・フォード」
内容紹介:
素粒子からブラックホールまで、奇妙で驚きに満ちた量子世界をひもとく画期的入門書。この1冊で現代物理学の本質がわかる!
事象は確率に支配され、複数の状態が重ね合わさり、粒子は生成と消滅を繰り返す―古典物理学の世界観を覆す奇妙で驚きに満ちた量子世界。その全体像を見事に描き出し、量子物理学の最前線へと誘う。
すべては確率に支配され、複数の状態が重ね合わさり、粒子は生成と消滅を繰り返す──古典物理学の世界観を覆す奇妙で驚きに満ちた量子世界。考え抜かれた101の項目でその全体像を見事に描き出し、量子物理学の最前線へと誘います。
”初めての人には「一冊読むならぜひこれを!」と、物理学者には「項目を見たら、きっと読みたくなりますよ」と申し上げたい”。(監訳者・青木薫氏による巻末解説より)
2014年3月刊行、424ページ。
著者について:
ケネス・フォード
1926年生まれ。理論物理学者。ジョン・ホイーラーのもとでPh.Dを取得。ブランダイス大学、カリフォルニア大学アーバイン校、マサチューセッツ大学などで学部長などを歴任。1987年から93年まで米国物理学協会会長を務めた。
理数系書籍のレビュー記事は本書で357冊目。
通っている歯科医院の先生からお借りしたものだ。いまいち納得できない解説があるので、ぜひ読んでから教えてほしいということなのだ。せっかくだから1冊まるごと読むことにした。
ブルーバックス本のなかで、本書はレベルが高いほうである。量子物理学というくくりで量子論、量子力学、素粒子物理学の想定問答集のような本。解説は文章が中心で図版はあまりない。420ページの本で101の質問に答えているのだから、質問1つあたり平均4ページを割いていることになる。
部の構成は次のとおり。それぞれの部にどのような質問がなされているかは、記事の末尾に記しておいた。
I 原子より小さい世界
II 原子核の奥へ
III 量子世界の距離、時間、速さ
IV 何が量子化されるのか
V 原子と原子核
VI 原子核のしくみ
VII 素粒子
VIII 素粒子の不思議なふるまい
IX 相互作用
X 量子世界の保存則
XI 波と粒子
XII 波と確率
XIII 量子物理学とテクノロジー
XIV さまざまなスケールでの量子物理学
XV 量子物理学に残された謎
読者の推奨レベルとしては大栗博司先生の「
重力とは何か」や「
強い力と弱い力」を読んだだけでは少し足りず、さらに南部陽一郎先生の「
クォーク 第2版」を読み終えたあたりの方にちょうどよい。
また、大学レベルの量子力学や場の量子論、素粒子物理の入門的な教科書で勉強中の方が副読本としてお読みになるのにもぴったりしている。
各質問に対する回答は、かなり深く切り込んでいるので「ああ、このように理解すればよいのか!」と感心することしきり。この分野の科学教養書を何冊も読んでいる人でも満足いただける本なのだ。
たとえば電子の波動性を示したド・ブロイの式 λ=h/p の説明が素晴らしかった。「
12歳の少年が書いた 量子力学の教科書: 近藤龍一」では「しかしながら、ここでE=mc^2を使って導出するのは間違いだ。光子の質量mは0だからこの式は使えない。正しい導出は次のページのようにして行なう。」と書いたが、本書では(質量のある)陽子を衝突させる加速器を引き合いにして、アインシュタインの式 E=mc^2 を使った説明をしている。
また原子核物理学に関する解説は、とてもためになった。原子核の中での陽子と中性子、電子の挙動を詳しく解説した教養書は初めてである。核分裂、核融合は特に詳しく解説されている。
V 原子と原子核
- 線スペクトルとは何ですか、そこから原子について何がわかりますか
- 元素の周期表はなぜ周期的になっているのですか
- 重い原子も軽い原子も、大きさがほぼ同じなのはなぜですか
- 原子核の内部で、陽子と中性子はどんな運動をしているのですか
- 原子番号、原子質量とは何ですか
VI 原子核のしくみ
- 周期表にはなぜ終わりがあるのですか
- 放射能とは何ですか
- なぜ中性子は原子核のなかだと安定しているのに、単独だと不安定なのですか
- 核分裂するとなぜエネルギーが放出されるのですか
- 核融合でもエネルギーが放出されないのはなぜですか
そして本書の監修者の青木薫さんが巻末にお書きになっているように、日々お世話になっている量子テクノロジーや、ミクロのスケールにとどまらず、日常のスケールや宇宙スケールであらわれる量子現象を取り上げ、最先端の話題と未来への展望を語っている。量子力学に関する本はけっこう読んでいるという人にも、このあたりの話は新鮮に感じられるのではないだろうか。というのも、一般向けの量子力学の本では、不確定性原理やシュレーディンガーの猫といった原理的な部分にフォーカスされることが多く、テクノロジーの話題にまで手が回らないということになりがちだからだ。
翻訳のもとになった原書はこれである。原書は2012年10月刊行なので「
ヒッグス粒子発見」の後だ。日本語版は2014年3月に刊行された。
「
101 Quantum Questions: What You Need to Know About the World You Can't See」(
Kindle版)
![]()
著者のケネス・フォードは、本書の中にもたびたび登場する伝説の物理学者ジョン・ホイーラーのもとで博士号を取得した物理学者である。1987年から93年まで米国物理学協会の会長を務めた。退任後は高校の教壇にも積極的に立ち、近年はサイエンス・ライターとしても活躍している。
つまり、本書は教育をライフワークとして位置付ける著者が、長年にわたり大学生や高校生に教えるなかで培ったノウハウを惜しみなく投入し、ライターとしての経験を生かしてまとめあげた力作なのである。
歯科医の先生の質問について
歯科医の先生が腑に落ちなかった件だが、本書の368ページから始まる「プランク長さとは何ですか。量子の泡とは何ですか。」という93番目の質問について、次のようなことを僕に聞いてきた。
「プランク長さというのが自然界で最小の長さだとして、その半分の長さを考えることに意味があるのか?それがわからない。本書での説明はどこか逃げている、答をズバリ書いていない気がする。」
プランク長さは、光速cとニュートンの重力定数G、プランク定数hという自然界の3つの基礎的定数から計算でき、プランク長さはプランクによるアイデアだ。またこの他、次のような物理量が知られている。
上からプランク温度、プランク質量、プランク時間、プランク長さ、プランク・エネルギー、プランク密度
![]()
これらは物理定数を全て 1 にするような単位系にするために考えられたものだ。これに関しては広江克彦さんが「
プランク単位系」というページでお書きになっている。つまり計算上の便法として導入されたのだ。だから、プランク長さに物理的意味があるかどうかとは別の話である。
「量子泡」のアイデアを思い付いたのはジョン・ホイーラーである。ミクロの世界になればなるほど時空は泡立っているという時空概念だ。この「仮説」の根拠は、プランク長さや量子力学の不確定性原理である。
また自然のスケールの階層に関しては「
大栗博司先生の超弦理論入門」でも取り上げられ、自然の階層には終わりがある、つまりこの世界にはそれ以上分割できない時間や空間があるかもしれないとお書きにになっている。(つまり仮説である。)しかし、弦理論や超弦理論では弦を記述するための背景場に実数という連続量であらわされる座標が必要であることを強調しておきたい。
![]()
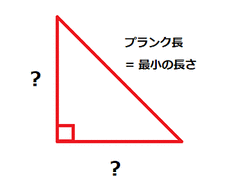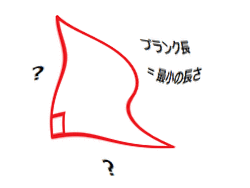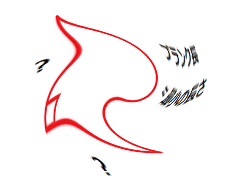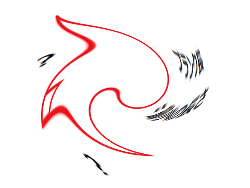
もしプランク長さが最小の長さだとしたら、どのようなことになるのか、簡単な例で説明してみよう。斜辺がプランク長さの直角二等辺三角形を考えてみる。
![]()
底辺や高さはプランク長さより短いはずだ。(高さ=斜辺/√2)つまり、直角二等辺三角形は存在できない。これを突き詰めれば、私たちが慣れ親しんでいるユークリッド幾何学が成り立たず、三平方の定理も使えないから「距離」が定義できなくなってしまうのだ。
一般相対性理論でも量子泡による効果でもよいのだが、極端に曲がったとしても空間がなめらかである限り、状況は同じである。この画像では渦巻き型に変形させてみた。スマートホンの方は画像をクリックし「元のサイズで見る」とアニメーションで見ることができる。
![]()
つまり最小の長さが存在すると、これまでの幾何学とは全く異なる新しい幾何学が必要になるのである。
さて、時空はなめらかに連続しているのではなく不連続、離散的だと考えるのはどうだろうか?この仮説もプランク長さや量子力学の不確定性原理に基づいている。
時空の量子化は半世紀以上前の
ハートランド・スナイダーに始まるが、 最近は非可換幾何学の流行により、 量子時空が多くの研究者の興味を惹いている。「
アラン・コンヌの非可換幾何学」もその例である。
「
ループ量子重力理論」も離散化した量子時空をベースにした理論だ。僕がこれまでに読んだのは「
ループ量子重力入門:竹内薫」と「
明解量子重力理論入門:吉田伸夫」の2冊。超弦理論も量子重力理論のうちのひとつである。次は「
初級講座 ループ量子重力:樺沢宇紀」を読みたい。
![]()
また、大栗博司先生は時空の不連続性とは別の視点から「
量子もつれが時空を形成する仕組みを解明~重力を含む究極の統一理論への新しい視点~」という発表をされている。
時空の離散化、量子化に関しては、次の資料をお読みになるとよいだろう。
一般相対論と量子論を繋ぐ、量子幾何学とは?
https://blog.goo.ne.jp/sonokininatte55/e/1a172a06b2d2fb2a6e5b489049c12546
山口哲先生のページ
http://www-het.phys.sci.osaka-u.ac.jp/~yamaguch/j/research.html
量子優先の原理と時空構造(京都大学、中西穰先生、2006年)
http://www.kurims.kyoto-u.ac.jp/~kyodo/kokyuroku/contents/pdf/1524-7.pdf
時空の原子を追うループ量子重力理論(日経サイエンス)
http://www.nikkei-science.com/page/magazine/0404/loop.html
いずれにせよ量子時空やプランク長さは、あまりにも小さく、物理的に意味があるかどうかは、仮説の段階であり、物理的に測定できるものではない。測定できないから物理的な意味がないとまでは言わないが、プランク長さをもとにした議論をするのは注意が必要だ。
プランク長さについて、広江克彦さんは「
プランク単位系」というページの「伝言ゲーム」という箇所で、次のようにお書きになっている。このページをお読みになるのがいちばんよさそうだ。
「プランク長さが我々の手に届くどんな物理現象とも掛け離れた極微のスケールなので、誰もまだ検証しようもないし、神秘性を帯びてしまって、話にどんどん尾ひれが付いてゆく。」
プランク長さの物理的意味を問うことに意味がないのであれば、歯科医の先生が考えた「プランク長さの半分」は、なおさらである。計算としては半分にできるが、物理的な意味は今のところなさそうだ。
プランク長さは測定できないが、プランク定数の値であれば光速cと万有引力定数Gとプランク定数hから計算できるほか、実験して求めることができる。これがその実験器。Amazonは何でも売っている。
プランク定数マニアの方は、こちらからお買い求めいただきたい。
「
プランク定数 実験器 U10700-115」
![]()
この製品と実験方法の詳細は、次のページでお読みいただける。
プランク定数:阻止電圧法を使って,プランク定数の値を求める
https://www.3bs.jp/physics/experiment/atom-expt/ue5010200.htm
関連ページ:
プランク定数の測定(滋賀総合教育センター)
http://www.shiga-ec.ed.jp/www/contents/1440578636412/files/kiki_phys_10.pdf
プランク定数の測定(津山工業高等専門学校)
http://www.tsuyama-ct.ac.jp/ippan/H21_hokoku/H21_sato1.pdf
LEDを用いたプランク定数の測定実験の試行
https://www.jstage.jst.go.jp/article/pesj/57/4/57_KJ00005929327/_article/-char/ja/
ブログ執筆のはげみになりますので、1つずつ応援クリックをお願いします。
![にほんブログ村 科学ブログ 物理学へ]()
![人気ブログランキングへ]()
![]()
![]()
![]()
![]()
![]()
「
量子的世界像 101の新知識: ケネス・フォード」
![]()
はじめに 量子世界のものの見方
I 原子より小さい世界
- そもそも量子とは何ですか
- 量子物理学の法則はどこで成り立つのですか
- 対応原理とは何ですか
- 原子はどれくらいの大きさですか
- 原子の内部はどうなっているのですか
- 原子の内部はほとんど空っぽの空間なのに、なぜ物質は固いのですか
- 電子の大きさはどれくらいで、内部はどうなっているのですか
II 原子核の奥へ
- 原子核の大きさはどれくらいで、内部はどうなっているのですか
- 陽子と中性子の大きさはどれくらいで、内部はどうなっているのですか
- プランク定数とは何ですか
- 光子とは何ですか
- 光電効果とは何ですか
- 基本粒子、複合粒子とは何ですか
- 標準模型とは何ですか
III 量子世界の距離、時間、速さ
- 量子的な距離スケールとはどういうものですか
- こんなに違う、4つの力が及ぶ範囲
- 粒子はどれくらいの速さで動きますか
- 量子的な時間スケールとはどういうものですか
- E=mc^2とは何をあらわしているのですか
- 電荷とは何ですか
- スピンとは何ですか
IV 何が量子化されるのか
- 物理量が量子化されるとはどういうことですか
- 運動状態とは何ですか
- 励起した原子は同じ原子が別の状態にあるだけですか、それとも別の原子になったのですか
- 量子数とは何ですか
- 量子飛躍とは何ですか
- 確率は量子物理学においてどいう役割を果たしているのですか
- 量子世界において何か確実なことはあるのですか
V 原子と原子核
- 線スペクトルとは何ですか、そこから原子について何がわかりますか
- 元素の周期表はなぜ周期的になっているのですか
- 重い原子も軽い原子も、大きさがほぼ同じなのはなぜですか
- 原子核の内部で、陽子と中性子はどんな運動をしているのですか
- 原子番号、原子質量とは何ですか
VI 原子核のしくみ
- 周期表にはなぜ終わりがあるのですか
- 放射能とは何ですか
- なぜ中性子は原子核のなかだと安定しているのに、単独だと不安定なのですか
- 核分裂するとなぜエネルギーが放出されるのですか
- 核融合でもエネルギーが放出されないのはなぜですか
VII 素粒子
- レプトンとは何ですか。そのフレーバーとは何ですか
- ニュートリノにもいくつかの種類があるのですか
- ニュートリノには質量があるのですか。ニュートリノ振動とは何ですか
- 素粒子にはなぜ3世代しかないのですか
- 電子はどれも同じだとどうしてわかるのですか
VIII 素粒子の不思議なふるまい
- 素粒子はどのように種類分けされているのですか
- クォークの特徴は何ですか。なぜ単独で見つからないのですか
- 複合粒子は何種類あるのですか
- すべての粒子はフェルミ粒子かボース粒子なのですか。この2種類はどう違うのですか
- ボース-アインシュタイン凝縮とは何ですか
- ボース粒子、フェルミ粒子はなぜそのように命名されたのですか
IX 相互作用
- ファインマン図とは何ですか
- ファインマン図の重要な特徴は何ですか
- ファインマン図は、強い力、弱い力、電磁力の相互作用をどのように図式化していますか
- 粒子が崩壊するとはどういうことですか
- 散乱とは何ですか
- 散乱や崩壊の前後で保存されるのは何ですか
- 散乱や崩壊で変わるものは何ですか
X 量子世界の保存則
- 量子世界でも大きなスケールでも成り立つ四大保存則
- 量子世界だけで成り立つ絶対的な保存則はありますか
- TCP定理とは何ですか
- 部分的にしか成り立たない保存則とは何ですか
- 部分的にしか成り立たない対称性の原理とは何ですか
- 法則を破らなければ、どんなことでも起こりうるのですか
- 対称性と不変性と保存の概念はどう関係するのですか
XI 波と粒子
- 波と粒子はどこが同じで、どこが違うのですか
- ド・ブロイの式とは何ですか
- 波は量子の塊とどう関係しているのですか
- 電子の波動性と原子の大きさはどう関係しているのですか
- 回折、干渉とは何ですか
- 二重スリット実験とは何ですか
- トンネル効果とは何ですか
XII 波と確率
- 波動関数とシュレーディンガー方程式
- 波と確率にはどのような関係があるのですか
- 粒子はなぜ1ヵ所にじっとしていることができないのですか
- 不確定性原理とは何ですか
- 不確定性原理と物質の波動性
- 重ね合わせとは何ですか
- 量子世界を理解するのに波は絶対に必要ですか
XIII 量子物理学とテクノロジー
- どうやって粒子を光速近くまで加速するのですか
- どうやって高エネルギー粒子を検出するのですか
- レーザーとはどのようなしくみですか
- 電子は金属のなかでどのようにふるまうのですか
- 半導体とは何ですか
- pn接合とは何ですか。なぜそれがダイオードなのですか
- ダイオードにはどういう用途があるのですか
- トランジスタとは何ですか
XIV さまざまなスケールでの量子物理学
- 蒸発するブラックホール
- 太陽の中心部で量子物理学はどのように働いているのですか
- 超伝導とは何ですか
- 超流動とは何ですか
- ジョセフソン接合とは何ですか
- 量子ドットとは何ですか
- クォーク・グルーオンプラズマとは何ですか
- プランク長さとは何ですか。量子の泡とは何ですか
XV 量子物理学に残された謎
- 無次元数137
- エンタングルメント(量子もつれ)とは何ですか
- ヒッグス粒子はなぜ重要なのですか
- 弦理論とは何ですか
- 観測問題とは何ですか
- どうして量子なのですか
表A.1 レプトン
表A.2 クォーク
表A.3 力の粒子
表A.4 おもな複合粒子
表B.1 乗数(ヘクト、キロ、メガ、ギガ、...)
表B.2 おもな大きさ(物理量)
人名さくいん
事項さくいん
監修者解説(青木薫)