日経サイエンス 2018年2月号特集：AIの新潮流

December 30, 2017, 12:37 am

≫ Next: Square root 234,256 using abacus (Half-multiplication table method 5)

「日経サイエンス 2018年2月号特集：AIの新潮流」

気になる記事が４つあったので、この号は買って読んでみた。Twitterでも話題になっているからお買いになった方が多いことだろう。

子どもの脳に学ぶAI　A.ゴプニック（詳細）
アルファ碁ゼロの衝撃　加藤英樹（詳細）
仮面ライダーの方程式　白石直人（詳細）
日本版「量子」コンピューターの選択　古田彩（詳細）

記事別に感想を残しておこう。この号の詳細は、次のページでご確認いただける。

日経サイエンス　2018年2月号　特集：AIの新潮流
http://www.nikkei-science.com/page/magazine/201802.html

子どもの脳に学ぶAI　A.ゴプニック

タイトルを見て英会話教材の「スピードラーニング」を思い出してしまい、可笑しかった。「赤ちゃんが言葉を学ぶときのように、英語を聞き流すだけで習得できます。」がこの教材のキャッチフレーズだ。

冗談はさておき、人間の脳を模倣するアプローチは、昔からあったのではないかと思っていたから、何が新しいのだろうと思って読んだ。最近の機械学習はディープラーニングのようにボトムアップの手法とベイズ法のようにトップダウンの手法の２つがあり、両者は競合しているそうだ。どちらも子供が自然に行なっている学習方法を不完全ながら真似ているのだという。どちらにしても長所と短所があり、満足のいく結果が得られるのはまだ先なのだという印象を持った。

そもそも僕は、人工知能は人間の脳を必ずしも模倣しなくてもよいのではないかと思っている。この記事で興味をもったのは、むしろ記事の間に挿入されていた「AIのブラックボックス化問題」のほうだった。この問題を解決すべく進行している富士通研究所、NEC、トヨタ・リサーチ・インスティチュートの取り組みの紹介が参考になった。やはりAIはブラックボックスのままではいけないのだ。

アルファ碁ゼロの衝撃　加藤英樹

アルファ碁ゼロのニュースは、僕にとっても衝撃的だった。そしてこの人工知能がチェスや将棋も指すようになったというニュースは衝撃の第２波となっていた。対局型のゲームの世界のこととはいえ、人工知能が過去の対局歴をまったく参考にせず、勝手に能力を上げていく世界がこんなにはやく来てしまったのかと身震いした。

でもこの記事を読んで少し安心した。記事をお書きになったのは囲碁ソフトZenを開発しているチームの代表者である。アルファ碁ゼロに対しても見方が手厳しい。ニュースで発表されるのは、都合がよいことばかりのことが多い。そして、制限や制約があっても後になってから発表されることがある。アルファ碁ゼロに関しても、それは同じだった。

アルファ碁ゼロがどのようなモデルで囲碁をマスターしたか、どのようにして対局するかを、実際に行われた何度かの対局を例にとって、ソフトウェアとハードウェアの側面から解説している。将棋AIと囲碁AIの違いのあらましを知ることができてよかった。

仮面ライダーの方程式　白石直人

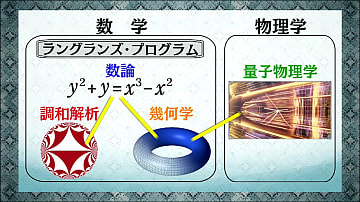
仮面ライダーの放送で、毎回物理の数式が映されていることは知っていたが、学部レベルの物理学だけでなく、最先端の理論で使われる数式があったのは、この記事で知った。お書きになったのは、この番組で数式を担当されている白石直人先生である。記事には「公開鍵暗号」のしくみと「蔵本転移」、「ゆらぎの定理」が詳しく解説されている。第14話までに登場した数式は次のとおり。

第1話：ケナード・ロバートソン不確定性関係
第2話：アーサー・ケリー・グッドマン不確定性関係
第3話：シュレディンガーの猫とレゲット・ガーグ不等式
第4話：特殊相対性理論のローレンツ変換
第5話：重力波
第6話：メタマテリアルのクローキング
第7話、第8話：公開鍵暗号
第9話、第10話：ドラゴン曲線とフラクタル次元
第11話：蔵本転移
第12話：カオス写像とリャプノフ指数
第13話、第14話：ゆらぎの定理

僕が子供の頃、NHKのみんなのうたの「算数チャチャチャ」に感化されたのが、理系選択のひとつのきっかけになったことは記事に書いたことがある。

この番組を見る子供たちに数式の呪文をかけて、この世界には自分の知らないことがまだまだたくさんあることを知っておいてもらうのは大事だと思った。番組で映される数式は、子供たちの「好奇心の種」になってほしい。

日本版「量子」コンピューターの選択　古田彩

このコンピュータのニュースを見たときは、報道を鵜呑みにしていたから、すごいことになったと驚いたわけだが、その後、専門家の間で交わされたツイートを見て、浮かれ過ぎていた自分を少し反省した。この記事をお書きになった古田彩先生のツイートも読んでいたから、記事の内容は予想できていた。でも、あらためて整理された形で読むと、この問題の扱いの難しさがよくわかる。うかうかしていると日本は海外に先を越されてしまう。「急いては事を仕損じる。」、「急がば回れ。」という諺が頭をよぎった。

とはいうものの研究者や責任者にとって実績を上げるのは必須である。お金がかかんでくると物事は歪められてしまうのだなと、あらためて思うのだ。先日逮捕されたスパコン社長のことも否応なく連想してしまう。

このように泥臭い事態になってしまったのは、日本だからなのか、海外でも事情は似たり寄ったりなのか、僕にはよくわからない。

この記事でためになったのは、日本版「量子コンピュータ」の原理が詳しく解説されていること、そしてどのような意味でこれが量子コンピュータとはいえないかがわかることだ。今後このコンピュータが使われ、現在のスパコンより優れていることが証明され、実際に問題解決に役立つのを示すことができれば、結果オーライとなるのだろう。

記事を読んでいちばん問題だと僕が思ったのは、ImPACTのプログラム・マネージャーの山本喜久氏が「量子コンピュータは実現しない」と思っていらっしゃることである。

ブログ執筆のはげみになりますので、１つずつ応援クリックをお願いします。

「にほんブログ村」では、「科学ブログ人気ランキング」と「注目記事ランキング（科学）」をくらべることでランキングを不正な手段を使って上げているブログがすぐわかるように作られている。不正行為はこのページのいちばん下に設置されたフォームから通報できる。（不正クリックの例）

「日経サイエンス 2018年2月号特集：AIの新潮流」

特集：AIの新潮流
機械学習
子どもの脳に学ぶAI　　A. ゴプニック
コンピューター囲碁
アルファ碁ゼロの衝撃　　加藤英樹

物理学
仮面ライダーの方程式　　白石直人

量子情報
日本版「量子」コンピューターの選択　　古田彩

惑星科学
間近で見た冥王星　ニューホライズンズがとらえた素顔　　S. A. スターン

発生
胎盤の不思議　　A. アーレバッカー／S. J. フィッシャー

農業
微生物と環境を生かすバイオーム農業　　M. ブロードフット

特別リポート
世界の科学情勢2017　合理性の危機
科学否定の根底にあるもの　　語り：K. ヘイホー
割れるヨーロッパ　　I. フェスパー
中国の動機　　L. ビリングズ

ダイジェスト
サイエンス考古学
原子力経済／自動車輸出の大市場／ハイヒール／凧型気球／爆発物／厳格な家庭

フロントランナー挑む
超高エネニュートリノで宇宙のロマン探る　　石原安野（千葉大学）

NEWS SCAN
●海外ウォッチ

新設計の量子ビット／プレート移動の始まりはいつ？／煙くさいワイン／舌打ち音言語が少ない理由／細胞再プログラムの新技術／食物の脳作用／ニュース・クリップ／レジを変えて食習慣を変える／トカゲのしっぽ振り／太陽嵐で破滅？

From nature ダイジェスト
雷が引き起こす光核反応

科学の森
「誰もしないことをやれ！」は創造の源泉　　和田昭允

ANTI GRAVITY
リスによるチャンク化　　S. マースキー

パズルの国のアリス
トランプ王国の故宮を復元せよ　　坂井公

グラフィック・サイエンス
お隣の系外惑星

ブックレビュー
『サルは大西洋を渡った』渡辺政隆

『デザイナー・ベビー』水島希

＜連載＞森山和道の読書日記　ほか

Information
次号予告
SEMICOLON
今月の科学英語

↧

Square root 234,256 using abacus (Half-multiplication table method 5)

December 30, 2017, 7:07 am

≫ Next: 開平と開立（第35回）：234,256の算盤による開平（半九九法5）

≪ Previous: 日経サイエンス 2018年2月号特集：AIの新潮流

[Set 234,256 on Mr. Square root]Zoom

[Japanese]

We will continue from where we ended in the last article, the actual solutions to calculate Square root using abacus. Today's example is Half-multiplication table method (Hankuku method), root is 3-digits case. We require root reduction in the steps. Please check the Theory page for your reference. You can check the Index page of all articles.

Square root methods: Double-root method, Double-root alternative method, half-multiplication table method, half-multiplication table alternative method, multiplication-subtraction method, constant number method, etc.

Abacus steps to solve Square root of 234,256
(Answer is 484)

"1st group number" is the left most numbers in the 2-digits groups of the given number for square root calculation. Number of groups is the number of digits of the Square root.

234,256 -> (23|42|56) : 23 is the 1st group number. The root digits is 2.

Step 1: Place 234256 on CDEFGH

Step 2: The 1st group is 23.

Step 3: Square number ≦ 23 is 16=4^2. Place 4 on B as the 1st root.

Step 4: Subtract 4^2 from the 1st group 23. Place 23-4^2=07 on CD.

Step 5: Focus on 74256 on DEFGH.

Step 6: Divide 74256 by 2. Place 37128 on DEFGH.

Step 7: Divide 37 on DE by the current root 4.

Step 8: 37/4=9 remainder 1. Place 9 on C as 2nd root.

Step 9: Place remainder 01 on DEE.

Step 10: Cannot subtract 9^2/2 from 11 on EF. 9 is excessive root. Place 9-1=8 on C.

Step 11: Give back the current root 4 to E. Place 1+4=5 on E.

Step 12: Subtract 2nd root^2/2 from 51 on EF. Place 51-8^2=19 on EF.

Step 13: Divide 192 on EFG by the current root 48.

Step 14: 192/48=4 remainder 0. Place 4 on D as 3rd root.

Step 15: Place remainder 000 on EFG.

Step 16: Focus on 8 on H.

Step 17: Subtract 3rd root^2/2 from 8 on H. Place 0 on H.

Step 18: Square root of 234256 is 484.

Final state: Answer 484

Abacus state transition. (Click to Zoom)

Next article is also about Half-multiplication table method, more difficult example.

Related articles:

How to solve Cube root of 1729.03 using abacus? (Feynman v.s. Abacus man)
http://blog.goo.ne.jp/ktonegaw/e/cff5d6e7ecaa07230b9cc7af10b23aed

Index: Square root and Cube root using Abacus
http://blog.goo.ne.jp/ktonegaw/e/f62fb31b6a3a0417ec5d33591249451b

Please place your mouse on the buttons and click one by one. These are blog ranking sites.

↧

開平と開立（第35回）：234,256の算盤による開平（半九九法5）

December 30, 2017, 7:22 am

≫ Next: 新年おめでとうございます。

≪ Previous: Square root 234,256 using abacus (Half-multiplication table method 5)

「開平はん」に234,256を置いたところ拡大

[English]

前回に続き、算盤での開平の手順を解説する。今回も半九九法で、根が３桁で過大根が生じ途中で根を還元するケース。理論編も参考にしていただきたい。全体の目次はこのページを開くと見ることができる。

開平（平方根）：倍根法(2商法)、倍根法別法、半九九法、半九九法別法、乗減法、定数法(折衷法) 、過大数開平、省略開平など

算盤による234,256の2乗根の解法（答は484）

第１群の数とは平方根を求める数を２桁ずつ区切り、いちばん大きい（いちばん左）の２桁のことである。群の数が根の桁数となる。

234,256 -> (23|42|56) : 23が第１群の数、根の桁数は3

手順1: 234256をCDEFGHに置く。

手順2: 第1群は23。

手順3: 23以下の平方数は16=4x4。4を初根としてBに立てる。

手順4: 23-4^2=07をCDに置く。

手順5: DEFGHの74256に注目する。

手順6: 74256を二分する。すなわち74256/2=37128をDEFGHに置く。

手順7: DEの37を既根4で割る。

手順8: 37/4=9余り1。商9をCに置き、次根とする。

手順9: 余り01をDEに置く。

手順10: EFの11から9^2/2は引けないから9は過大根。次根9から1を引いた8をCに置く。

手順11: 既根4の1倍をEに還元。すなわち1+4=5をEに置く。

手順12: EFの51から次根^2/2を引く。51-8^2/2=19をEFに置く。

手順13: EFGの192を既根48で割る。192/48=4余り0

手順14: 商4を得てDに置き、第3根とする。

手順15: 余り000をEFGに置く。

手順16: Hの8に注目する。

手順17: Hの8から第3根^2/2を引く。8-4^2/2=0をHに置く。

手順18: 平方根は484と求まる。

最終状態：答 484

珠の状態推移を表にすると次のようになる。（クリックで拡大）

次回も半九九法による開平だが、もう少し難しい例をとりあげる。

関連記事：

ファインマン v.s. 算盤の達人：ファインマン先生に立方根計算の雪辱を果たそう
http://blog.goo.ne.jp/ktonegaw/e/89a0b907577f03ef6132cf9664bdcddb

目次：算盤による平方根、立方根の計算（開平、開立）
http://blog.goo.ne.jp/ktonegaw/e/bb0449f357398a2c24026f33af7f70ee

ブログ執筆のはげみになりますので、１つずつ応援クリックをお願いします。

↧

新年おめでとうございます。

December 31, 2017, 7:00 am

≫ Next: 映画『インセプション（2010）』

≪ Previous: 開平と開立（第35回）：234,256の算盤による開平（半九九法5）

２０１８　元旦
読者のみなさまへ

新年おめでとうございます。昨年は当ブログをお読みいただきありがとうございました。

数えてみたところ昨年は２０４本の記事を投稿していました。そして２０１６年以前は

２０１６年は１０５本
２０１５年は１１１本
２０１４年は９６本
２０１３年は１００本
２０１２年は１１４本
２０１１年は１４５本
２０１０年は１１８本
２００９年は１１５本
２００８年は２００本
２００７年は１４８本
２００６年は１５４本
２００５年は６７本

の記事を投稿していましたから、昨年の記事数は例年の２倍に見えます。けれども２０４本のうち６５本は算盤の記事ですので、算盤以外の記事数は１３９本です。

そして昨年は10月に次の記録を達成しました。

祝：累計400万アクセス達成！
http://blog.goo.ne.jp/ktonegaw/e/d158b87317d6ce8838e6258663f28c0c

物理学と数学が基本であることに変わりはありませんが、昨年はこれ以外に人工知能や量子コンピュータの本の感想記事が加わりました。また将棋や算盤の記事も書くようになりました。反面、電卓関連や電子工学の記事が減っています。（関心が薄れたわけではありません。）

趣味の読書に目標や予定をたてても、そのとおりに進まないことがわかったので、今年も興味の趣くままに読書や勉強を進めてまいります。

楽しい正月をお過ごしください。みなさまの健康とご活躍を心より願っております。

初詣は「とね神社」へお越しください。お賽銭クリックはこちらからどうぞ！それぞれのランキングサイトに投票が行われます。

おみくじはここで引けます。今年も運勢を占ってみましょう。（画像をクリックして進みます。）

↧

映画『インセプション（2010）』

January 2, 2018, 1:44 am

≫ Next: 夜のウォーキング、その後10（累積9000Km）

≪ Previous: 新年おめでとうございます。

Official Site (English, for PC)

みなさんは初夢をご覧になっただろうか？今日紹介するのは夢にまつわる映画である。昨年末に友達からもらったDVDで観てみた。

映画『インターステラー（2014)』はクリストファー・ノーラン監督の作品だが、こちらも彼が監督・脚本・製作を担当した。2010年のアメリカのSFアクション映画で、第83回アカデミー賞では作品賞、脚本賞、撮影賞、視覚効果賞、美術賞、作曲賞、音響編集賞、録音賞の8部門にノミネートされ、撮影賞、視覚効果賞、音響編集賞、録音賞を受賞した作品である。

映画『インセプション』オフィシャルサイト - 英語サイト、Flash使用
http://wwws.warnerbros.co.uk/inception/mainsite/

「夢の世界と現実がかかわりを持っていたら？」というのは、どなたも空想したことがあるだろう。また、恋愛中の人は「夢で逢えたら」などと夢想することもあるだろう。さらに「夢の中で夢を見る」という経験をしたことがある人もいるかもしれない。

この３つをSFとして映像化したのがこの作品である。何とロマンチックな。。。いやいや、そうではない。これはアクション映画なのだ。

この映画の感想をネットで検索すると、「難しくてついていけない」とか「頭がこんがらがる」というコメントが目につく。確かにそうなのだ。通常の映画でさえ、登場人物が多いと配役どうしの関係や、シーンの背景事情を把握するまでは集中して見なければならない。登場人物の善人と悪人の区別が配役の顔つきではっきりしていればよいのだが、そうでなければ把握するまで時間がかかる。この作品がそうなのだ。

そしてさらに、この映画の理解のハードルを上げているのが「夢の世界」であり、現実と夢の世界で同じ人物が登場して、しかも数分ごとに夢と現実のシーンが切り替わる。時間的な前後なのか夢と現実の切り替わりなのか混乱するのである。そして映画の途中から「夢の中で夢を見る世界」が持ち込まれ、現実、夢、夢の中の夢の３つの層が互いに関連を持ちながら同時進行してしまうのだ。これで混乱しないほうがどうかしている。

第１層：現実の世界
第２層：夢の世界
第３層：夢の中の夢の世界

だから全部理解するまでには２、３回観ることをお勧めする。

あらすじはウィキペディアの記事を引用すると次のようになる。

「ドミニク・コブ(通称コブ)とアーサーは、標的の無意識に侵入する軍の実験段階の技術を用いて、標的の夢から重要情報を引き出す、「引き出し人」と呼ばれる産業諜報員(産業スパイ)だった。ところが、今回の標的である日本人実業家サイトウは、コブが、標的の無意識にある考えを植え付ける(inception)、遂行困難な仕事をこなせるか試したと言う。

病気である競争相手モーリス・フィッシャーが経営するエネルギー複合企業を破滅させるために、サイトウは、コブに、モーリスの息子で後継者であるロバートに父親の会社を解体させるよう納得させる事を依頼する。サイトウは、見返りとして、コブの殺人容疑を取り消して、コブが子供達の待つ家に戻れるように影響力を行使する事を約束する。コブは依頼を引き受け、口達者な「なりすまし人」イームス、夢を安定させる強力な鎮静薬を調合するユスフ、亡き妻の父であるステファン・マイルズ教授の助けで勧誘した、夢の中に設置する迷宮を設計する建築学科の学生アリアドネで組織を組む。アリアドネは、入り込んだコブの夢の中で、亡き妻モルが侵略的に投影されているのを知る。」

この文章で理解できるとしたら、あなたは相当物分かりのよい人だ。（僕は映画を観終えてから理解できた。）

夢を共有するためにはアタッシュケースに入れられた装置を使う。その装置から伸びる電極をそれぞれ手首につけて、何人かが眠ることで夢の世界を共有することができる。

夢の中では現実の１０倍の速さで時間が進む。（そして第３層の夢ではさらにその１０倍の速さで時間が進むという設定だ。）夢から現実に戻るときは夢の世界で死ねばよいことになっている。ただし、夢の中でも痛みなどの感覚はそのままなので、死ぬのは恐ろしい。まして銃で撃たれたりするわけだから。。。そして鎮静薬をうってから眠ると、夢の中で死んでも現実世界には戻れないのだ。これがストーリーに緊張感をもたせる設定として効いている。

夢の世界では何でも起きてしまうのが見どころのひとつ。夢と現実を区別するのは空間が曲がったり、無重力状態になったりするなどの超常現象があるかどうか、そして周囲の群集（エキストラのような人たち）が自分たちに向ける敵意の視線をもっているかどうかで判断することができる。これは遠方の街並みがせり上がってくるシーンである。

開始から最初の１時間は、このように不思議で奇妙な映像に驚きながら、ストーリーの進行を理解していく。夢の中のシーンは変幻自在であるとともに、ロケーションについても自由だ。東京や京都近郊も含めて世界６か国でロケが行われている。夢と現実のパラレルワールド、そして場所についてのテレポーテーションが理解のハードルを上げていく。

ようやく把握できたかな？と思い始めるのは開始からおよそ１時間後、しかしそれもつかの間、登場人物たちはとんでもない危機に見舞われることに。。。アクション映画の始まりだ。わけのわからない所を残しつつ、ハラハラドキドキ。なんだか凄いことになってきたなぁと、見続けてしまうわけだ。

ヒューマンドラマとしての側面もある。主人公のドミニク・コブ（レオナルド・レオナルド・ディカプリオ）には自殺してしまった奥さんがいて、夢の世界ではむかし彼女と過ごした家での生活がある。切ない。。。また、現実世界は長い間会うことができない幼い息子と娘がいるのだが、夢の中で子供たちの幻影を何度も目撃して、現実世界での再会を切望している。奥さん
がなぜ自殺してしまったのか、コブは子供たちと再会できることになるかは、映画を観てのお楽しみとしておこう。

空間が曲がったり時間の進みが変わるのは相対性理論を思い出させるし、夢と現実はパラレルワールド、そして夢の中の場所が切り替わるのはテレポーテーションを思い起こさせる。理系的要素たっぷりの映画だし、心理的な葛藤や幻想とノスタルジー、そしてアクション映画としてのスピード感も満喫できる。ぜひご覧になっていただきたい。

映画『インセプション』予告編

しかしながら。。。しかしながらである。残念に思ったことが２つあった。

ひとつはアジア人差別があるかな？と感じてしまったこと。そしてもうひとつはアメリカ映画ならではの暴力シーンに関してだ。

クリストファー・ノーラン監督が、俳優の渡辺謙さんを高く評価していることを知っている
上での感想であるが、この映画で銃で撃たれたり、瀕死の重症を負わされて痛々しい姿をさらすのは渡辺謙さんが演じる「斉藤（映画字幕ではサイトーと表記）」だけなのだ。誘拐されたエネルギー複合企業の御曹司ロバート・フィッシャーでさえも血は流さない。アメリカ人だけカッコよく描かれていると感じてしまった。

もうひとつは暴力的なシーンへの嫌悪感である。夢の世界の住民や敵が襲ってくるのだが、コブを始め登場人物は何の躊躇もなく彼らを殴り倒したり、撃ち殺したりする光景が何度も映される。こういう暴力シーンを見慣れてしまうから、アメリカ人はこの世界には善人と悪人しかいないという単純思考を植え付けられてしまうのだと思った。アメリカ社会で警官が、銃を持たない容疑者や無抵抗の黒人を殴ったりする背景に、人種差別以前の「善悪二元論」があると思うのだ。

夢の世界を映像化したり、他人と共有できたら、この映画に少し近い体験ができるのだろう。そのように空想するのは楽しい。しかし、もしこれが実現したらと思うと少し怖くなる。

視覚で得た刺激を脳が感じている映像を取り出す実験がすでに始まっている。夢の世界の映像ではないにしても、脳の中にある動画映像の可視化が成功しつつあることは、次の記事で紹介したことがある。夢の映像化の第一歩だ。

NHKニューヨーク白熱教室：第４回　変貌する“心の未来”
http://blog.goo.ne.jp/ktonegaw/e/af868d9e78346e91a6f2056201a0afa3

数学の世界は「イデア界」にあるのかもしれない。数学のイデア界は幻想的な夢のように思える。そして「夢の中で夢を見ること」というキーワードで思い浮かぶのは「改訂版微積分のはなし〈下〉：大村平」で使われていたこの挿絵だ。イデア界がイデア界を無限に含んでいるようなもの。

現実の世界では解くことができない微分方程式をラプラス変換して、もう一つの世界（夢の世界？）に移すと、単純な分数方程式に変わってしまう。変換後の世界では簡単に解けてしまうのだ。そして解けた結果を逆ラプラス変換して現実の世界に戻してあげる。するとそれは現実の世界での解になっているのだ。

もし与えられた微分方程式が（より難易度の高い）高階の方程式であれば、ラプラス変換を何度も行なってから（つまり夢の中で夢を見てから）解いて、元の世界に戻してやれば、不思議なことに問題は解けてしまうのだ。

現実の生活には人間関係や仕事上の問題、恋愛問題など頭を悩ます問題がいくつもある。夢の中で解決するのは簡単だろうし、それで現実の問題が解決できたらよいのにと思ってしまう。ところが数学の世界ではこれに似たようなことを、ときどき経験するのだ。

また、次の例も共通点があるのかもしれない。「フェルマーの最終定理」という「数論」の世界の問題は難問であり、350年もの間、数学者たちの頭を悩ませ続けた。この定理は「調和解析」の世界の「志村・谷山・ヴェイユ予想」が1995年にワイルズとテイラーによって証明されることによって解決されたのだ。(1995年のワイルズによる証明はこのPDFで読める。）

この図は「数論」と「調和解析」の世界がつながっていることだけでなく、「幾何学」の世界ともつながっていることを示している。この３つはイデア界にある数学だ。

そしてさらにこのイデア界は、あろうことか「量子物理学」の世界ともつながっているそうなのだ。「イデア界が現実世界と関わりをもっているらしい」というのは、にわかに信じられないかもしれない。

数学と物理学の境界とは、空想上のイデア界と現実世界の国境のことである。この国境は存在しないという予想のもとに研究が進んでいるのが「ラングランズ・プログラム」である。詳しいことは、次の記事をお読みいただきたい。

感想： NHK数学ミステリー白熱教室
http://blog.goo.ne.jp/ktonegaw/e/b0d53d030bf82e8016a1071fadb16063

映画の話からだいぶ脱線してしまったが、僕にとって「夢と現実のつながり」から連想するのは、このようなことである。

映画『インセプション（2010）』をご覧になりたい方は、次のリンクからどうぞ。

Blue-ray, DVD　Amazonビデオ

英語台本
「Inception: The Shooting Script」

関連記事：

映画『インターステラー（2014)』
http://blog.goo.ne.jp/ktonegaw/e/58711fc5335ca00f51a5d22df3f6cc58

ブログ執筆のはげみになりますので、１つずつ応援クリックをお願いします。

↧

夜のウォーキング、その後10（累積9000Km）

January 3, 2018, 10:27 pm

≫ Next: AI 人工知能の軌跡と未来 (別冊日経サイエンス)

≪ Previous: 映画『インセプション（2010）』

2013年4月7日から今日までに歩いた累積距離

2013年3月8日に始めた夜のウォーキング。ナイキのランニングアプリで歩いた距離を記録始めたのは300Km歩いた１か月後からだった。今日、累積距離が9000Kmに達したので記事として記録しておこう。

累積8500Kmを超えたところでNikeのアプリでの距離計測はやめている。アプリを毎晩使っていたためiPhone6のバッテリー劣化がいちじるしかったからだ。そのため昨年11月初めに機種変更を余儀なくされた。（参考記事：「iPhone 6からiPhone Xに機種変更」）

歩くルートはいつも同じだから、いちいち計測する必要はない。歩くたびに距離を足し算していけばよいだけである。

というわけなので、この記事トップのスクリーンショット画像は加工（偽造）して作ったものだ。

累積メータが8000Kmに到達したのは昨年の7月16日なので1000Km歩くのに172日（5.6ヶ月）かかっている。月あたり177Kmのペース。

これまでの記録はこうなる。

累積5000Km達成: 2016年2月1日
累積6000Km達成: 2016年7月15日
累積7000Km達成: 2017年2月3日
累積8000Km達成: 2017年7月16日
累積9000Km達成: 2018年1月4日

累積8000Kmまでは2000Km/年のペース（月に154Km）で歩いていたが、今回はだいぶペースが上がった。これは天候に恵まれたことと、サボる日がほとんどなかったからだ。

最近は歩きながらワンセグテレビを見るのはやめにして、主にラジオを聞いている。フランス語や英語の講座やラジオニュースだ。紅白歌合戦もラジオで聴いていた。

あと、ときどきradikoのタイムフリーで「壇蜜の耳蜜」も歩きながら聴いている。壇蜜さんのファンのことは「ミツラー」ではなく「ミツシタン」と呼ぶのだそうだ。ファンであることを隠しておくのが無難という意味か。w

この数年は脂肪燃焼というより、むしろ健康維持のためという目的に切り替えている。サボる日もあるが、継続が何より大事だ。

関連記事：

１日人間ドック（2010年）
http://blog.goo.ne.jp/ktonegaw/e/78d08050074f97baefb45084b0e936e2

ウォーキングと夜桜（2013年3月）:
http://blog.goo.ne.jp/ktonegaw/e/055b88c503e142d7b9559e5965de5550

夜のウォーキング、三軒茶屋へ（2013年3月27日）
http://blog.goo.ne.jp/ktonegaw/e/cfd8a6fb66f8d236da95531fd108d8cf

夜のウォーキングのその後（2013年6月6日）
http://blog.goo.ne.jp/ktonegaw/e/65eb0d670f88ee2225670772ad03793e

夜のウォーキング、その後２（2013年7月1日）
http://blog.goo.ne.jp/ktonegaw/e/a64b260d065375c77a79c2839dc414be

夜のウォーキング、その後３（2013年8月27日）
http://blog.goo.ne.jp/ktonegaw/e/7da6bbf0006e187662cf2cf1822b82fe

１日人間ドックとウォーキング（2014年4月2日）
http://blog.goo.ne.jp/ktonegaw/e/630184969180751eecfdfcfeb6ff54c0

夜のウォーキング、その後４（累積3000Km）: 2014年11月15日
http://blog.goo.ne.jp/ktonegaw/e/6e55742ebae984371eed25cc70de75bb

夜のウォーキング、その後５（累積4000Km）: 2015年5月27日
http://blog.goo.ne.jp/ktonegaw/e/31b8bd0070d5d2853a7515efc7ac0e2e

夜のウォーキング、その後６（累積5000Km）: 2016年2月1日
http://blog.goo.ne.jp/ktonegaw/e/20cde6adec555ae73da5ab19156ae257

夜のウォーキング、その後７（累積6000Km）: 2016年7月15日
http://blog.goo.ne.jp/ktonegaw/e/1c78ee3fbdf5077b17b69596746ebe63

夜のウォーキング、その後８（累積7000Km）: 2017年2月3日
http://blog.goo.ne.jp/ktonegaw/e/1b73972a971a66c79eac24535750f931

夜のウォーキング、その後９（累積8000Km）: 2017年7月16日
http://blog.goo.ne.jp/ktonegaw/e/b7de5cb526634b0f4ab88eed68c78d06

ブログ執筆のはげみになりますので、１つずつ応援クリックをお願いします。

↧

AI 人工知能の軌跡と未来 (別冊日経サイエンス)

January 5, 2018, 12:12 am

≫ Next: Square root 323,761 using abacus (Half-multiplication table method 6)

≪ Previous: 夜のウォーキング、その後10（累積9000Km）

「AI 人工知能の軌跡と未来 (別冊日経サイエンス)」

内容紹介：
隆盛期と冬の時代を繰り返してきた人工知能はいま第三次ブームを迎えた。AI研究の飛躍を支えるのはディープラーニングと呼ばれる手法だ。
大量のデータの特徴を高い精度で捉えて、これをデータに生かす方法で、音声認識や画像解析で応用が始まっている。一方、人間の能力を超えたAIが、人の生活を激変させる「シンギュラリティ」も現実味を帯びてきた。
本書では、1950年代にコンピューターチェスを提唱したシャノン、人工知能の父ミンスキー、日常生活の中でのロボットの可能性を述べたビル・ゲイツなどの執筆記事を主軸に、IBMのワトソンの実力分析や、韓国のプロ棋士イ・セドルを破ったAlphaGoの強さの秘密など、最新の話題を加え、AI研究の軌跡と未来を描く。
2016年11月刊行、127ページ。

理数系書籍のレビュー記事は本書で353冊目。

「Newton(ニュートン) 2018年 01 月号：ゼロからわかる人工知能」、「日経サイエンス 2018年2月号特集：AIの新潮流」に続き、本書を読んでみた。まえがきも含めて、記事それぞれの簡単な内容紹介と感想を書いておこう。

詳細はこちらである。

AI 人工知能の軌跡と未来 (別冊日経サイエンス)
http://www.nikkei-science.com/page/sci_book/bessatu/51216.html

まえがき：逃げなかった水--ブームの先の未来へ

本書を編集した竹内郁夫先生による「まえがき」だ。現在に至るまでのAIの歴史を概説した後、本書に掲載されている記事を順に紹介している。記事の数が多いので、お目当ての記事やお宝記事をあらかじめおさえておくとよいだろう。

論争--機械はものを考えるか-- NO: プログラムは記号でしかない

AIは物を考えることができるかという問いに対して「No」の立場から論証している。あまりピンとこなかった。「考える」ということの定義が不確かだから、そもそも問いとして成り立たないのではないかという気がする。「中国語の翻訳」ができたからといって中国語をAIが理解したとは思えないというのは納得できた。Google翻訳は外国語への翻訳ができるからといって、言語を理解しているとか、考えているとかは言えないと思う。

論争--機械はものを考えるか--YES: 統合化が心をつくる

AIは物を考えることができるかという問いに対して「No」の立場から論証している。AIが脳を
模倣し、処理を並列化したりニューラル・ネットワークを使用すれば「考える」ことができるようになる可能性は否定できないという主張。これもどうもピンとこなかった。「考える」ということの定義が不明確である限り、この論争は不毛だと思った。

人工知能の意識を測る

AIは意識を持つことができるか？という高度な問いかけであるが、内容はたいしたことがなかった。意識を持っているかどうかの判定基準として、花瓶がパソコンモニターの前に置かれている写真をAIに見せて、それを変だと言うかどうかによって、意識をもっているかどうかを判定すればよいという説明。花瓶ではなくキーボードが置かれているのが普通だからである。この判定を行うには厖大な背景知識と知識の間のつながりを理解している必要がある。高度な問いに対して肩透かしをくらった気持ちになった。この問を真剣に考えなければならない未来はかなり先のことだと思う。

ロボットは地球を受け継ぐか

医療技術の発展により人間の平均寿命は延びる。しかし生物としての死は避けられないことで、どんなに医療技術が発展しても人間はせいぜい120歳までしか生きられないことがDNAに組み込まれているそうだ。さて、その先に何があるのか？それは脳も含めて身体の器官を人工物に置き換えて延命するのである。あまりにも先の未来の話なので、おそらく僕が生きている間には実現しないだろう。軽く読み流すだけにさせていただいた。

スーパーAI恐るべし？

AIが進化して人類の良きパートナーになるかどうか？そのためにAIに求められる「AI三原則」を提唱している記事。AIが人類を滅ぼす存在にはなってはならないという意見に僕は賛成するが、物事の発展は「原則」のような制限をつけても、守られないことがわかりきっている。たとえば「ロボット三原則」は理想だと思うが、現実には殺人ロボットが開発されているのだし。問題はそれがロボットやAIが完全に自立したときだ。

人工知能の可能性を信じグランドチャレンジを主導：松原仁

松原仁先生がこれまでされてきた研究を紹介する記事。コンピュータ将棋、AI小説、ロボカップなど。とても楽しく読むことができた。

チューリングの忘れられた研究

本書のお宝記事の１つめ。これまであまり知られていなかったが、アラン・チューリングは「B型組織マシン」というニューラル・ネットワークの論文を書いていたこと、「ハイパー計算」という画期的な分野で革新的な概念を生み出していたことが紹介されている。この記事はとても興奮した。天才は100年後を見通しているのだ。

あなたの好み探します：実力高まる人工知能

検索エンジンや推奨エンジンをより知的で的確なものにするために、機械学習の手法を利用する技術の紹介記事。「過剰適合問題」を解決するために「正則化」と呼ばれる手法を使ってモデルの複雑化を抑えるという。実用に則した内容なので参考になった。ｊ

爆発的に進化するディープラーニング

ディープラーニングによるパターン認識技術の解説が大半を占める。将来の技術の例として最後に「再帰型ニューラルネットワーク」が紹介される。大変参考になった。しかし概要だけではつかめない。より具体的なことを他の本で学んでみたいと思った。

チェスを指す機械

本書のお宝記事の２つめ。1950年にクロード・シャノンが書いた記事の翻訳である。チェスをする機械はどのようにして実現すればよいのか。短い記事ながらとても具体的に天才のアイデアが語られている。とても面白かった。やはり天才の先見の明は凡人をはるかに凌いでいる。

コンピュータはチェス名人に勝てるか

1990年の日経サイエンスの記事の転載。この時点で世界チェスチャンピオンのカスパロフはIBMの「ディープブルー」に敗北していた。この記事ではディープブルーの前に開発された「ディープソート」の開発やアルゴリズム、そして「ディープブルー」でどのような改善がなされたのかをソフト、ハード両面から解説している。AIチェスに関心のある人にはうれしい内容である。

どうして囲碁はこんなに急に強くなったのか？

DeepZenというAI囲碁ソフト開発チームの代表、加藤英樹先生による記事。囲碁名人のイ・セドル九段にAlphaGoが勝利した後に書かれたものだ。したがってAlphaGo Zeroのことは書かれていない。この記事ではAlphaGoがどのような経緯で開発され、どのようなアルゴリズムを採用しているかが詳しく解説されている。チェスや将棋のAIと囲碁のAIは何が違うのかということが具体的にわかってよかった。実際の対局の盤面を使って解説しているが、囲碁のルールを知らないからよくわかなない部分が残った。囲碁の初歩的なルールを学んでみようかどうか迷っている。この記事読んでから「日経サイエンス 2018年2月号特集：AIの新潮流」に掲載されている加藤先生の記事でAlphaGo MasterとAlphaGo Zeroの解説をお読みになるとよいだろう。

ここまできた機械翻訳

機械翻訳の手法の歴史を概説した後、現在取り組まれている統計的な手法を採用した機械翻訳システムを解説している。この分野を僕は詳しく知っているので、ざっと読み流すにとどめた。

発見するコンピューター：論文の山から宝を探す

論文検索、テキストマイニングの最新技術の紹介記事。生物学の論文を例に解説していた。医学や医療、生物学、薬学、化学など固有名詞が厖大な分野では、威力を発揮すると思った。反面、物理学や数学には利用価値があまりないのではという気がした。

自分で推論する未来型ウェブ

現在のウェブの仕様にコンピュータ向けのデータやページを追加することで、セマンティックウェブに変えることができる。具体的にはXMLやRDFで「意味を埋め込む」ことになる。ウェブページの検索はより的確かつ便利に使えるようになるのだろう。「言うは易し」だと僕は思った。意味を埋め込むのは手間がかかる。どのようにすれば効率的に意味を付加できるのだろう？そのような疑問が残った。

ウェブサイエンスの誕生

「ウェブサイエンス」という新しい学問領域の紹介記事。ウェブページやSNS、ブログなど多様なサービスが生まれ、利便性の向上とプライバシーやセキュリティの問題が生じた。ウェブの特性が生じるしくみと社会のためにどのよに利用あるいは抑制できるかをこの記事は具体例をあげて探求している。内容が少し古いと感じたのだが、案の定2009年に書かれた記事の転載だった。

IBM Watsonの歩み：クイズ番組への挑戦からコグニティブ・コンピューティングへ

本書のために書き下ろされた新しい記事である。IBMのWatsonがクイズ番組で人間に勝利したのは2011年である。ワトソンがどのようにして実現されたのかが詳しく解説されている。その当時僕はこのAIの意義が理解できていなかった。Watsonのような技術をコグニティブコンピューティングというのだそうだ。ナレッジベースの進化形ということだろう。この技術が医療に応用されることで、癌の検査や治療の選択肢を医師に提供するシステムとして活用されている。2011年当時の手法は、現在個別にはかなりの部分がディープラーニングなど最近の手法に代替されるようになっているそうだ。

ホームロボット時代の夜明け

ホームロボットというと、まず「ルンバ」を思い浮かべるのだが、今後IoTの普及にともなって、さまざまなロボットが登場するのだと思う。この記事によれば現在のロボット産業は30年前のパソコン業界が抱えていたのと同じ課題に直面しているそうだ。つまり共通の標準とプラットフォームが欠けているから、マシン制作をいちから始めないといけない。ロボット用のOSやプログラミング言語、分散処理技術が開発されるのだとこの記事には書かれている。どうなのだろう？と僕は思った。ロボットの目的はそれぞれ違うのだから、共通のOSはともかく、共通の言語などを決めることができるのだろうか？そのような疑問が残った。

心を持つロボット

この記事は読むに値しなかった。生と死を経験しない機械が感情をもつと認めてはならないという根本的な思想を僕は持っているからだ。老人ホームで高齢者を癒すPepperやぬいぐるみロボットがいることは受け入れられるし、感情をもっているように偽装することは可能だと思う。高齢になって判断力が衰えるとそのように思い込みやすい。人間の判断力など五十歩百歩なのだから、AIが高度に発達すれば普通の人間でも感情を持っていると信じてしまうだろう。しかし、それを感情だと認めてはならないというのが僕の考えだ。現実の人間は予想通りに感情をあらわすときもあれば、予想と反対の感情をあらわすこともある。それは人生経験や考え方で違ってくる。そして個性や人生経験を人工知能に埋め込んだとしても、ロボットが表現するものを感情と認めてはならないと僕は思うのだ。

仮にAIに「人格」を持たせたいのであれば、感情のうち都合のよいところだけ切り取って済ませるわけにはいかない。嫉妬や怒り、憎しみ、恨み、殺意までネガティブな感情も必須であり、ポジティブな感情とワンセットだ。どれも欠かせるわけにはいかないと思うのだ。

余談：大原麗子さんや壇蜜さんを完璧に模倣するアンドロイドができたら、僕は買ってしまうだろうが、だとしても「彼女」たちに感情が備わっていると認めないと思う。少なくとも最初のうちは。

余談２：みんながみんな、お気に入りのアンドロイドを連れて歩くようなことになったら、社会はぐちゃぐちゃ、人間関係は混乱の極みになることだろう。また有名歌手のライブなどはアンドロイドでいつでも代用できるし、若き日のビートルズのライブだって手軽に体験できる。CDを聴いたり、VRで楽しむのと大差ない。また、エリック・クラプトンから毎週ギターのプライベート・レッスンを日本語でしてもらうこともできる。最初のうちは嬉しいだろうが、そのうち飽きてくる。つまり貴重な体験として得られる喜びがなくなってしまうのだ。望みを叶える先には退屈な世界が待っているような気がする。

研究するロボット

「学者」として機能するAIは実現するのだろうか？とてつもない話である。せいぜい、人間の学者が研究を進めるための補助として活用するのが関の山だろうなと思った。50年先でも無理だと思う。しかし100年、200年先はわからない。僕は生きていないだろうから、考えるのはやめようと思った。

関連記事：

日経サイエンス 2018年2月号特集：AIの新潮流
http://blog.goo.ne.jp/ktonegaw/e/2acba888748409964bbc2b13f4163437

Newton(ニュートン) 2018年 01 月号：ゼロからわかる人工知能
http://blog.goo.ne.jp/ktonegaw/e/daf3a744f940e92c0277e9e5e576604b

ブログ執筆のはげみになりますので、１つずつ応援クリックをお願いします。

「AI 人工知能の軌跡と未来 (別冊日経サイエンス)」

まえがき：逃げなかった水--ブームの先の未来へ

論争--機械はものを考えるか
- NO: プログラムは記号でしかない
- YES: 統合化が心をつくる

人工知能の意識を測る
ロボットは地球を受け継ぐか
スーパーAI恐るべし？
人工知能の可能性を信じグランドチャレンジを主導：松原仁
チューリングの
忘れられた研究
あなたの好み探します：実力高まる人工知能
爆発的に進化するディープラーニング
チェスを指す機械
コンピュータはチェス名人に勝てるか
どうして囲碁はこんなに急に強くなったのか？
ここまできた機械翻訳
発見するコンピューター：論文の山から宝を探す
自分で推論する未来型ウェブ
ウェブサイエンスの誕生
IBM Watsonの歩み：クイズ番組への挑戦からコグニティブ・コンピューティングへ
ホームロボット時代の夜明け
心を持つロボット
研究するロボット

↧

Square root 323,761 using abacus (Half-multiplication table method 6)

January 6, 2018, 9:31 pm

≫ Next: 開平と開立（第36回）：323,761の算盤による開平（半九九法6）

≪ Previous: AI 人工知能の軌跡と未来 (別冊日経サイエンス)

[Set 323,761 on Mr. Square root]Zoom

[Japanese]

We will continue from where we ended in the last article, the actual solutions to calculate Square root using abacus. Today's example is Half-multiplication table method (Hankuku method), root is 3-digits case. We require 9 as root in the middle of calculation. Please check the Theory page for your reference. You can check the Index page of all articles.

Square root methods: Double-root method, Double-root alternative method, half-multiplication table method, half-multiplication table alternative method, multiplication-subtraction method, constant number method, etc.

Abacus steps to solve Square root of 323,761
(Answer is 569)

"1st group number" is the left most numbers in the 2-digits groups of the given number for square root calculation. Number of groups is the number of digits of the Square root.

323,761 -> (32|37|61) : 32 is the 1st group number. The root digits is 2.

Step 1: Place 323761 on CDEFGH.

Step 2: The 1st group is 32.

Step 3: Square number ≦ 32 is 25=5^2. Place 5 on B as the 1st root.

Step 4: Subtract 5^2 from the 1st group 32. Place 32-5^2=07 on CD.

Step 5: Focus on 73761 on DEFGH.

Step 6: Divide 73761 by 2. Place 36880.5 on DEFGHI.

Step 7: Divide 36 on DE by the current root 5.

Step 8: 36/5=6 remainder 6. Place 6 on C as 2nd root.

Step 9: Place remainder 06 on DE.

Step 10: Focus on 68 on EF.

Step 11: Subtract 2nd root^2/2 from 68 on EF. Place 68-6^2=50 on EF.

Step 12: Focus on 508 on EFG.

Step 13: Divide 508 on EFG by the current root 56.

Step 14: 508/56=9 remainder 4. Place 9 on D as 3rd root.

Step 15: Place remainder 004 on EFG.

Step 16: Focus on 405 on GHI.

Step 17: Subtract 3rd root^2/2 from 405 on H. Place 000 on GHI.

Step 18: Square root of 323761 is 569.

Final state: Answer 569

Abacus state transition. (Click to Zoom)

It is interesting to compare with the Double-root method.

Next article is also about Half-multiplication table method, more difficult example.

Related articles:

How to solve Cube root of 1729.03 using abacus? (Feynman v.s. Abacus man)
http://blog.goo.ne.jp/ktonegaw/e/cff5d6e7ecaa07230b9cc7af10b23aed

Index: Square root and Cube root using Abacus
http://blog.goo.ne.jp/ktonegaw/e/f62fb31b6a3a0417ec5d33591249451b

Square root 323,761 using abacus (Double-root method 7)
http://blog.goo.ne.jp/ktonegaw/e/e57e2bc935af3a511814efb2458b18f4

Please place your mouse on the buttons and click one by one. These are blog ranking sites.

↧

開平と開立（第36回）：323,761の算盤による開平（半九九法6）

January 6, 2018, 9:34 pm

≫ Next: 宝くじが当たったら (講談社文庫) ：安藤祐介

≪ Previous: Square root 323,761 using abacus (Half-multiplication table method 6)

「開平はん」に323,761を置いたところ拡大

[English]

前回に続き、算盤での開平の手順を解説する。今回も半九九法で、根が３桁で途中で9を立根するケース。理論編も参考にしていただきたい。全体の目次はこのページを開くと見ることができる。

開平（平方根）：倍根法(2商法)、倍根法別法、半九九法、半九九法別法、乗減法、定数法(折衷法) 、過大数開平、省略開平など

算盤による323,761の2乗根の解法（答は569）

第１群の数とは平方根を求める数を２桁ずつ区切り、いちばん大きい（いちばん左）の２桁のことである。群の数が根の桁数となる。

323,761 -> (32|37|61) : 32が第１群の数、根の桁数は3

手順1: 323761をCDEFGHに置く。

手順2: 第1群は32。

手順3: 32以下の平方数は25=5x5。5を初根としてBに立てる。

手順4: 32-5^2=07をCDに置く。

手順5: DEFGHの73761に注目する。

手順6: 73761を二分する。すなわち73761/2=36880.5をDEFGHIに置く。

手順7: DEの36を既根5で割る。

手順8: 36/5=6余り6。商6をCに置き、次根とする。

手順9: 余り06をDEに置く。

手順10: EFの68に注目する。

手順11: EFの68から次根^2/2を引く。68-6^2/2=50をEFに置く。

手順12: EFGの508に注目する。

手順13: EFGの508を既根56で割る。508/56=9余り4

手順14: 商9をDに置き、第3根とする。

手順15: 余り004をEFGに置く。

手順16: GHIの405に注目する。

手順17: GHIの405から第3根^2/2を引く。405-9^2/2=000をGHIに置く。

手順18: 平方根は569と求まる。

最終状態：答 569

珠の状態推移を表にすると次のようになる。（クリックで拡大）

同じ問題の倍根法での解法と比べてみてほしい。

次回も半九九法による開平だが、もう少し難しい例をとりあげる。

関連記事：

ファインマン v.s. 算盤の達人：ファインマン先生に立方根計算の雪辱を果たそう
http://blog.goo.ne.jp/ktonegaw/e/89a0b907577f03ef6132cf9664bdcddb

目次：算盤による平方根、立方根の計算（開平、開立）
http://blog.goo.ne.jp/ktonegaw/e/bb0449f357398a2c24026f33af7f70ee

開平と開立（第13回）：323,761の算盤による開平（倍根法７）
http://blog.goo.ne.jp/ktonegaw/e/d05c0a0943ab183e0dfef0690717feb4

ブログ執筆のはげみになりますので、１つずつ応援クリックをお願いします。

↧

宝くじが当たったら (講談社文庫) ：安藤祐介

January 6, 2018, 9:52 pm

≫ Next: フランス語の辞書はどれがいい？

≪ Previous: 開平と開立（第36回）：323,761の算盤による開平（半九九法6）

「宝くじが当たったら (講談社文庫) ：安藤祐介」（Kindle版）

内容紹介：
32歳、わくわく食品経理課勤務、独身。ごく普通のサラリーマン・修一の趣味は宝くじをバラで10枚買うこと。ところが今年、一等、2億円が降ってきた。あくまで堅実でつつましい生活を続けようとした修一の目の前に、急に現れた親戚、慈善団体に同級生。さらにネットに実名が流出、会社の電話が鳴りやまない! 最高の幸福が招いた大混乱、いったい誰を信じれば? ジャンボなドリーム、宝くじエンタテインメント!
2015年12月刊行、304ページ。

著者について：
安藤祐介
1977年、福岡県生まれ。早稲田大学政治経済学部卒業後、学習塾に入社するも過労で倒れて退職、2社目の酒類業界新聞社では試用期間で解雇通告を受ける。その後は営業職としてITベンチャー3社を渡り歩き、現在公務員。2007年、『被取締役新入社員』でTBS・講談社第1回ドラマ原作大賞を受賞。（著書を検索）

先日紹介した映画『インセプション（2010）』と同様、今回も「夢」にまつわる記事。

昨年末に３枚だけ買った年末ジャンボ宝くじのうち１枚が3000円当たった。ジャンボ宝くじはいつも３枚買っていて、昨年のハロウィンジャンボと一昨年の年末ジャンボは、それぞれ300円ずつ当たっている。ときどき3000円当たるので、過去の勝ち負けをならすと損も得もしていない。（運が強いほうだと思う。）

当せん番号

豆知識：宝くじでは「当せん」のようにひらがなで表記する。漢字だと「当籤（とうせん）」となって読めない人がでるからだ。「当選」は選挙で選ばれるときや、懸賞などで選抜されるときに使う。

１等の７億円が当せんする確率は、北海道全体で３枚だけ落ちてくる１円玉が頭にぶつかる確率くらいだとか、隕石に当たって死ぬ確率くらいだとか言われている。

ジャンボ宝くじの１等当せん確率は雷に撃たれるのと同じ!?
https://matome.naver.jp/odai/2140479404950634801

当せん確率や当せん金の期待値を考えたら、ナンバーズのほうがずっと有利なのだ。でも、僕がジャンボ宝くじを選ぶのは「夢を買う」からなのだろう。購入日から抽選会の日までワクワクしていられるからだ。

「１等が当たったらどうしよう？」、「どんなことが待ち受けているのだろうか？」そのような妄想に満たれて、過ごす数週間に対して払う対価だと思ったらハズレてもがっかりしない。僕が買うのは毎回３枚だけなのだから。

本書はこのような妄想をシミュレーションするための本である。完全なシミュレーション本であり、実際の当せん者の「その後の人生」を書いたドキュメンタリー本ではない。

もし、自分が同じテーマで小説を書くとしたらと考えると、ストーリーはかなり制限されてくると思った。テーマを自由に選べる小説と違い、１等の当せん後に予想されることはだいたい同じだからである。

- 当せん者はごく普通の一般庶民（会社社長や有名人であってはならない。）
- 当せんがわかったときの驚き
- 銀行での説明や手続き
- 秘密を守ることの難しさ
- 家族や親族の反応
- 「秘密はあり得ない」ことを思い知る
- 友達にばれてしまう
- 募金・寄付依頼の電話、断ると「それでも人間ですか！」と非難される
- 投資話、儲け話の電話
- 人間不信になる
- ネットに拡散、炎上してしまう。
- 嫌がらせや脅迫電話
- 借金や支払いの無心を受ける
- 同僚のやっかみ、人間関係の変化、交友関係の変化
- 飲み会やパーティー、結婚式、家の改築など増え続ける出費
- 詐欺にあったり闇金から強迫を受けたりする
- あっという間にお金がなくなる

つまり、この流れになることがほぼ決まっているのだ。この流れを守りながら、どれくらい面白い文章を書けるか、読者を楽しませることができるかが、作家の技量にかかってくる。このテーマの本に「意外性」を求めてはいけない。「宝くじが当たったら」は数ある小説のひとつのジャンル、お題目なのである。

読んでみたところ、まあまあ面白かった。小説としては上手に書かれている。本書で主人公が１等で受け取るのは２億円である。微妙な金額だ。32歳だから会社を辞めるまでの決断はできない。まさか当せんするとは思っていなかったから、どのように使ったらよいか大いに悩むわけである。

世の中には億単位の資産を持っている人がたくさんいるわけだから、２億円はたいした金額ではない。ちゃんと管理しようとすればできるのである。しかし、そのような大金を持ったことがない人だと、よほど注意しなければ同じような末路をたどることになるのだ。

当せんすることで不幸にならないようにと、1000万円以上の高額当せん者に渡されるのが「【その日】から読む本」とう小冊子。非売品である。（内容全文はこのページに公開されている。）

この冊子は、たまにヤフオクに出品されていて、相場はこのとおり。（画像クリックで拡大）

幸運な人だけが手に取れる【その日から読む本】とは？
https://matome.naver.jp/odai/2139381299063048901

宝くじ高額当せん者だけに配布される冊子に書かれた「驚愕の注意点」…不幸なトラブルも多数
http://biz-journal.jp/2017/01/post_17823.html

一般庶民がいきなり大金を手にすると、ろくなことにはならない。そうは言っても、現在のジャンボ宝くじの１等は７億円である。

もし７億円あったら、自分は何をするだろう？

ふたたび大学を受験して物理学を専攻し、研究者への道を目指してみたい。（趣味で博士課程、趣味でポスドク、趣味で物理学者をするのである。）時間がたくさんあるから「とね日記」も毎日更新することになるだろう。

実際はそうはならず、自堕落で贅沢な生活に流れてしまうのだろうなぁ。本書が示す不幸へのルートを脱して、本当の夢を追うのは相当むずかしそうだ。

宝くじに当たった人は人生変わったのか？高額当せん者6人の使い道
https://www.a9note.com/takarakuji-tousensha/

僕がいつもジャンボ宝くじを買っている店舗はこちら。（クリックで拡大）

宝くじボタンに１つずつ応援クリックをお願いします。（ブログランキング投票）

「宝くじが当たったら (講談社文庫) ：安藤祐介」（Kindle版）

プロローグ

第１章：ぼくは辞めません
第２章：吉事、千里を走る
第３章：３３歳で大ブレイク
第４章：持っちゃった人
第５章：札束でかがり火を焚く
第６章：諭吉のリトマス試験紙
第７章：ひとりぼっちのあいつ
第８章：人として人に迷う
第９章：それでも人しか愛せない

エピローグ

↧

フランス語の辞書はどれがいい？

January 7, 2018, 10:07 pm

≫ Next: マグネット将棋〝ミニ〟現代印（メーカー、製造年不明）

≪ Previous: 宝くじが当たったら (講談社文庫) ：安藤祐介

今朝はフランス語の授業をして過ごした。初心者のうちは辞書は特にいらないと僕は思っているのだけど、持っていればモチベーションが高まる人もいることだろう。

初心者から使える紙の辞書とスマホアプリを紹介しよう。

無料のオンライン辞書

単語の意味だけを知るのであれば、無料のオンライン辞書を活用するのがよいだろう。仏和・和仏の両方向で使えるし、発音もしてくれる。多言語対応であるが、フランス語の辞書として現在の語数は11万語である。

Glosbe - 多言語オンライン辞書
https://ja.glosbe.com/

無料のスマホアプリ（アプリ内で課金あり）

French English Dictionary

説明：無料のでということであれば、これがお勧め。仏英辞書だけでなく英仏辞書としても使える。有料オプションもあるが、差し当たり無料で使っていればよいだろう。

有料のスマホアプリ

仏和辞典、和仏辞典のアプリは有料版をお勧めする。（無料のは学習用にはお勧めしない。）

プチ・ロワイヤル仏和（第4版）・和仏（第3版）辞典

説明：入門者用の学習辞典。2010年に刊行された紙の仏和辞典、和仏辞典にアプリも追いついている。仏和と和仏がセットになっているのがよい。紙の辞典を２冊買うよりも安くてすむ。

クラウン仏和辞典第6版

説明： 2005年に発売された「クラウン仏和辞典第6版」のアプリ版。紙の辞書は第7版が2015年に出ているのでアプリは紙の辞書の版に追いついていない。また、和仏辞典は刊行されていない。

紙の辞書（初級者用）

紙の辞書は中古のものが安く買えることがある。アプリや電子辞書は便利だが、学習用に紙の辞書が優れているのは言うまでもない。

「【CD-Extra付】プチ・ロワイヤル仏和辞典第4版」

説明：上記アプリの書籍版。ショッキングピンクなのは箱だけで、中身は上品なホワイト。1792ページ、見出し語数43000。CD-ExtraのCD-ROM部分に本文全文と全動詞活用表を収録し、音声CD部分に発音解説、会話基本パターン、重要動詞の活用(暗唱の手本)を収録。中古本を買うときはCD-ROMの有無を確認したほうがよい。またこのシリーズには「プチ・ロワイヤル和仏辞典第3版」がある。箱はブラックで、中身は上品なホワイトだ。46000語を収録。用例・複合語・関連語が充実。

「クラウン仏和辞典第7版」

説明：2015年に発売された最新の仏和辞典。箱と中身は可愛らしいピンク色。1776ページ、見出し語数約6万3千項目、用例約8万を収録。より小型で携帯性のよい「クラウン仏和辞典第7版小型版」もある。小型版の箱と中身は水色。

紙の辞書（初級・中級・上級者用）

初級から上級者まで使える辞書は、分厚くなり持ち運びに不便だが、家で使うのなら以下のものがお勧め。

「ロワイヤル仏和中辞典第2版」

説明：2005年に発売された中型辞典。実物は「ロワイヤル仏和中辞典（辞書談義）」という記事でご覧いただきたい。2229ページ、見出し語9万語、用例12万件で、学習用としてはじゅうぶん。この辞書はPC版や電子辞書としても発売されている。残念ながら付属のCD-ROMが最新のWindowsに対応していない。（参考ページ）電子辞書は「発売情報：カシオ電子辞書 XD-G7200（2017年フランス語モデル）」に入っているので、この紹介記事をお読みいただきたいが、毎年2月に新モデルが発売されるので、来月まで購入するのは待ったほうがよいだろう。この辞書のアプリが発売されるのがいちばんよいのだが、カシオの電子辞書の売り上げが激減するから、アプリ版の発売はないと思われる。

「ディコ仏和辞典[新装版] 」

説明：2016年に発売。小型、中型辞典を含めていちばん新しく、顔文字ほか新語満載の充実した和仏辞典付き。仏和35000語+和仏7200語、1817ページ。発音・会話の音声はウェブから無料ダウンロード。（ダウンロードできるのは辞書ではない。）2009年に発売された初版の「ディコ仏和辞典」1817ページ、は中古本がとても安い。

なお2008年に発売された「プログレッシブ仏和辞典第2版」も中型辞典としてお勧めである。なぜなら、中古のものがとても安く手に入るからだ。1650ページ、3万5千語を収録。和仏インデックス付き。発音の解説や動詞活用などの音声をインターネット（小学館ランゲージワールド：http://l-world.shogakukan.co.jp/）で無償配信。図版や囲みも多数収録。

フランス語を専門としている人や長年教えている人は、辞書への思い入れが強く自分が使った思い出の辞書を勧めることが多い。フランス文学を学ぶのならば古い辞書でもよいのだが、語彙や語義は時代の変化にともなって変化していく。初学者は新しい辞書を使ったほうがよいというのが、僕の考えである。

紙の辞書がよいのか、アプリ版がよいのか、電子辞書がよいのかは、判断しにくいものがある。家で勉強することが多いのなら紙の辞書がいちばんよい。外で学ぶことが多いのならアプリや電子辞書が便利だ。紙の辞書でもCD-ROMが付属していたり、ダウンロード・サービスがあればノートPCに入れて持ち運べる。大切なのは「勉強を続けること」だ。そのために、どれを選択すべきかは、ご自身で決めるのがよいのだろう。

関連記事：

フランス語を教え始めた
http://blog.goo.ne.jp/ktonegaw/e/da69b2a85fb8e10b225867d3fe2731da

発売情報：カシオ電子辞書 XD-G7200（2017年フランス語モデル）
http://blog.goo.ne.jp/ktonegaw/e/edf8b147324b423c1e21e041ddf23dd9

Le Petit Prince （星の王子さま）
http://blog.goo.ne.jp/ktonegaw/e/cff1f935410e1d670ead5bade63f0a0d

ゴドーを待ちながら：サミュエルベケット
http://blog.goo.ne.jp/ktonegaw/e/9fb9147540f30317b405ab342e42a4c9

ウジェーヌ・イヨネスコ『授業』
http://blog.goo.ne.jp/ktonegaw/e/c688b8fd10e692fda6c08f81a80e23d7

発売情報：フランス語版「ファインマン物理学」の新版
http://blog.goo.ne.jp/ktonegaw/e/daf630deb00e6c315897d6f47ba3dd5a

発売情報： Le Petit Robert 仏仏辞典 2018年版
http://blog.goo.ne.jp/ktonegaw/e/af95cd2913db7377993a2f32e2a74118

Le Petit Robert 仏仏辞典 2017年版がiPhone/iPadアプリとして発売！
http://blog.goo.ne.jp/ktonegaw/e/c639abc6cfe45e1675d0a72181116e86

小学館ロベール仏和大辞典（iPhone / iPad アプリ）
http://blog.goo.ne.jp/ktonegaw/e/02af8bb1e929b8f415f7efc32a92bd56

ブログ執筆のはげみになりますので、１つずつ応援クリックをお願いします。

↧

マグネット将棋〝ミニ〟現代印（メーカー、製造年不明）

January 10, 2018, 3:29 am

≫ Next: 素数に憑かれた人たち～リーマン予想への挑戦～：ジョン・ダービーシャー

≪ Previous: フランス語の辞書はどれがいい？

マグネット将棋〝ミニ〟現代印拡大

今日紹介するのは、ほとんど出回ることがないレア物のマグネット将棋だ。新品のものは販売されていない。商品名は「マグネット将棋〝ミニ〟現代印」。パッケージには製造元の名前や住所が書かれていないので、メーカーや製造年は不明。「現代印」というのが、もしかするとメーカー名なのかもしれない。

磁石は駒の中央に配置しているから、成る前と後で盤へつく力はほぼ同じ。磁力はちょうどよい。

以下、写真をクリックすると拡大するようにしておいた。

ポケット将棋やマグネット将棋の相場価格は500円から2500円くらいだ。このように低価格の商品に高い品質を期待してはいけないのかもしれない。

それでもできるだけ良い品を持ちたい。そのような気持ちで8月に購入した将棋セットを「マグネット将棋を購入（大久保碁盤店）」という記事で紹介していた。しかし、この商品の駒の裏面が樹脂製のシールであることが不満だった。

ふだん利用しているカフェで、いつも将棋を研究している「カフェ仲間」のKさんが使っているマグネット将棋が気になっていた。もしできるなら同じ駒が欲しい。Kさんに聞いたところ、駒だけを知り合いからいただいたのでメーカーや商品名はわからないのだという。

6月くらいから探し続けて、ようやくヤフオクに出品されていることに気が付いた。製造されてからだいぶたっているようだが未開封である。裏面が黒文字かどうかはわからない。おそらくKさんの将棋駒はこれだろうと1000円で落札させていただいた。この商品を探している人は少なからずいることも、ネットで検索してわかった。

昨年8月に購入した磁石将棋（ハンディー）の駒。裏面は樹脂製のシールが貼られ、文字はシールに印刷されている。このシールで磁石を固定しているので、磁石は盤面に近い位置にあるから盤面にしっかり着く。駒が成って裏返しになると磁石は盤面から少し離れることになるが、磁力はじゅうぶん効いている。銀将だけ印刷がかすれているのが少し残念。

ベージュ色の「磁石将棋（ハンディー）」と黄色がかった「マグネット将棋〝ミニ〟」を比べてみよう。

マグネット将棋は低価格なものばかりだから、売り上げが期待できない。製造側にしても、Amazonやヤフオクにしても、商品名やメーカーの表示がいいかげんなものが多いのは、そのためだ。購入側からすれば、お目当ての商品が探しにくい。

通常サイズで木製の駒だと数万円から百万円くらいのものまで、高級なものがある。たとえば、これは45万円の駒。

マグネット将棋でも5000円から20000円の価格帯で、木製で書体にこだわった高級駒、あるいは樹脂製でも高級駒を模倣した商品が販売されたらよいのにと思うのは僕だけだろうか？

今回は、この商品を探している方への情報提供として記事を書かせていただいた。

マグネット将棋を検索： Amazon　ヤフオク　メルカリ

関連記事：

マグネット将棋を購入（大久保碁盤店）
http://blog.goo.ne.jp/ktonegaw/e/92637160014c1f22d52243eb3d23cbaf

将棋セット購入
http://blog.goo.ne.jp/ktonegaw/e/9f6ae58f79977e31a09fe5247a94bd3b

ブログ執筆のはげみになりますので、１つずつ応援クリックをお願いします。

↧

素数に憑かれた人たち～リーマン予想への挑戦～：ジョン・ダービーシャー

January 14, 2018, 3:18 am

≫ Next: 声でつづる昭和人物史～湯川秀樹（NHKラジオ第２）

≪ Previous: マグネット将棋〝ミニ〟現代印（メーカー、製造年不明）

「素数に憑かれた人たち～リーマン予想への挑戦～：ジョン・ダービーシャー」（Kindle版）

内容紹介：
フェルマー予想が解決された現在、整数論での次の標的であるリーマン予想に対して取り組んできた数学者の紹介を中心に、素数を知る魅力、取り組みの変遷などを、多くのエピソードを織り込みながら、非数学的な観点をベースに著述した数学ドラマ。奇数章で数学の直感的な説明、偶数章でその歴史的及び人間的なバックグラウンドを解説しています。
リーマン予想は、素数の分布に関する予想で、リーマンのゼータ関数の零点の実数部は1/2であるというもの。1900年にヒルベルトが提示した23の未解決問題及び2000年に米クレイ数学研究所が懸賞金付きで提示した7つの未解決問題の1つに挙げられています。年に1回は「証明した」という発表がされ、話題となる著名な予想。登場人物は、（19世紀から20世紀前半までの数学者を除いて）ピエール・ドゥリーニュ（1978年フィールズ賞）、アラン・コンヌ（非可換幾何学、1982年フィールズ賞）、アラン・チューリング（反例を見つけようとした）、アンドリュー・オドリツコ（後に暗号理論で著名）、ヒュー・モンゴメリ（整数論）、フリーマン・ダイソン（物理学者）、など。
2004年8月刊行、479ページ。

著者について：
ジョン・ダービーシャー（John Derbyshire）
イギリスで数学教育を受け、現在は米国在住のシステム・アナリスト。小説家でもある。

訳者について：
松浦俊輔
名古屋工業大学助教授を経て、翻訳家。名古屋学芸大学非常勤講師など。
訳書： Amazonで検索

理数系書籍のレビュー記事は本書で354冊目。

本書は2009年にNHKで放送された「素数の魔力に囚われた人々～リーマン予想・天才たちの１５０年の闘い～」の原作本、ネタ本である。下北沢の古書店で安いのを見つけたので購入した。

(動画を検索）（NHKオンデマンドで見る）

放送当時から本書は読みたいと思っていたが、およそ８年間手つかずのままだった。番組の内容は覚えているから、おさらい程度になるかなと思って読んだのだが、章が進むにつれてのめり込んでいく。数学物語として見事である。著者の技量はさすがだ。番組を見た直後に読むべきだったと少し後悔した。

数式が書かれた科学教養書という位置づけ。高校数学を学んだ人であれば、難なく読み通せるだろう。オイラーの公式を学び終えた高校生が、大学数学を先取りして複素関数論を学んでみたくなったとき、準備として前もって読むのがよい。数学ファンだけでなく、物理学ファンも大いに萌えることができる本だ。

奇数章は数学的な解説にあてられ、偶数章は素数定理やリーマン予想に取り組んだ数学者たちの伝記だ。リーマン以後、現代までの驚きと神秘に満ちた壮大なストーリー。

本書の主題は「素数定理」と「リーマン予想」

素数定理
https://mathtrain.jp/7theorem

リーマン予想の意味，素数分布との関係
https://mathtrain.jp/riemannyoso

ゼータ関数と素数が関連していることを示す式

ゼータ関数の非自明なゼロ点

ゼータ関数の非自明なゼロ点（「リーマンのゼータ関数の数値計算コード(複素平面)」から引用）

素数は小学生でも求められるほど計算は簡単なのに、素数と密接に結びついているゼータ関数は、複素領域でこれほど複雑なパターンの模様を生み出しているのは、実に神秘的である。

無限個あるというゼータ関数の非自明なゼロ点は次のようにすれば計算できるそうだ。

リーマンゼータ関数のゼロ点を手計算してみた
http://mattyuu.hatenadiary.com/entry/2016/10/02/134730

鳥肌が立ってきたのは、本書の４分の３あたりにさしかかったときだ。第18章の「数論と量子力学の出会い」からである。

ゼータ関数の非自明なゼロ点の間隔と原子核のエネルギー準位の間隔に関連があるのではないかというくだり。ゼロ点とエネルギー準位の間隔が完全に一致したわけではない。これはNHKの番組でも取り上げられていた。数学の世界の素数と現実世界の物質の振る舞いに、なぜ関係性が見られるのだろう？

番組で紹介されたのはこのあたりまでだが、僕は「たまたま両者の数式が一致しただけじゃないの？」と思っていた。

ところが本書では、この話が詳しく解説されるだけでなく、その後のことも語られている。鍵になるのが原子核のエネルギー準位にかかわる「エルミート行列」である。複素数を成分とするこの行列のことは大まかに解説されているので大丈夫。詳しく学びたければ「高校数学でわかる線形代数：竹内淳」をお読みになるとよい。

そしてもうひとつ鍵になるのが「ガウス分布」である。エルミート行列の複素成分をランダムにして、原子核のエネルギー準位の統計的分布を求めるのである。

そして得られたのはゼータ関数のゼロ点の統計的分布と原子核のエネルギー準位の統計的分布に、きわめて高い類似性が見られたという結果だ。現在はまだ「予想」のレベルなのだが、詳細は「モンゴメリー・オドリズコ予想」や「ゼータ関数の零点分布と量子カオス」をお読みいただきたい。本書ではこれらのページよりもずっと易しいレベルで解説がされている。

そして第１９章からは、それまでの章でひとまず途中ままにしておいた結果を総合して、素数の分布とゼータ関数の関係性の分析をさらに進める。究極の謎の解決へ向けて突き進むアプローチは、とてもアクロバティック数式変形を伴うが、私たちにも十分理解できる内容に抑えてある。

リーマン予想はまだ証明されていない。数学者たちがどのように考えているかが最終章で紹介される。この予想はおそらく正しいのだろうけれども、間違っている可能性だって残っているのだ。いったいどちらなのだろう？おそらく正しいのだろうと思うしかない。

自分が生きている間に解決するのだろうか？このブログをお読みになるような方だったら、誰もがそう思っていることだろう。

久々に興奮しながら読めた本だった。章が進むにつれて面白くなるので、最初がつまらなくても辛抱して読み続けてほしい。

本書には姉妹本がある。２冊合わせてどうぞ。

「素数に憑かれた人たち～リーマン予想への挑戦～：ジョン・ダービーシャー」（Kindle版）
「代数に惹かれた数学者たち：ジョン・ダービーシャー」

翻訳の元になった英語版は、それぞれこちら。

「Prime Obsession: Berhhard Riemann and the Greatest Unsolved Problem in Mathematics 」
「Unknown Quantity: A Real and Imaginary History of Algebra」

そして気になるのがこの本。コンパクトながら、上手にまとめてあるようだ。

「リーマン予想とはなにか全ての素数を表す式は可能か：中村亨」（Kindle版）

リーマン予想といえば黒川信重先生である。この２冊がとても気になっている。（黒川先生の本をAmazonで検索する。）

「リーマン予想を解こう ~新ゼータと因数分解からのアプローチ」（Kindle版）
「絶対数学の世界 ―リーマン予想・ラングランズ予想・佐藤予想」

さらに物理学徒であれば、この２冊が気になるはずだ。

「リーマン予想のこれまでとこれから」
「素数からゼータへ、そしてカオスへ」

１冊読むと、気になる本がとめどなくでてくるのだ。積読本がなくなることは絶対にない。楽しめる本は、まだまだたくさんあるのだとポジティブに考えることにしよう。

関連記事：

素数の魔力に囚われた人々～リーマン予想・天才たちの１５０年の闘い～
http://blog.goo.ne.jp/ktonegaw/e/c855d3c8628459df7371c2c53789c794

現代思想 2016年3月臨時増刊号総特集◎リーマン -リーマン予想のすべて-
http://blog.goo.ne.jp/ktonegaw/e/6216f2ff6057e8c3bfa2d4ca8e28d479

リーマン--人と業績： D.ラウグヴィッツ
http://blog.goo.ne.jp/ktonegaw/e/505069a0aa6932910a709a3eeaded988

幾何学の基礎をなす仮説について：ベルンハルト・リーマン
http://blog.goo.ne.jp/ktonegaw/e/22be602fe4cee385a9939c0869c511eb

ブログ執筆のはげみになりますので、１つずつ応援クリックをお願いします。

「素数に憑かれた人たち～リーマン予想への挑戦～：ジョン・ダービーシャー」（Kindle版）

プロローグ

第１部素数定理

第１章：カード・マジック
第２章：土壌と作物
第３章：素数定理
第４章：巨人たちの肩に乗って
第５章：リーマンのゼータ関数
第６章：大融合
第７章：黄金の鍵と改訂版素数定理
第８章：見いだされる価値
第９章：広がる定義域
第１０章：証明と転機

第２部リーマン予想

第１１章：数の体系
第１２章：ヒルベルトの第8問題
第１３章：複素関数を見る
第１４章：執着に捉えられて
第１５章：ビッグ・オーとメビウスのミュー
第１６章：クリティカル・ラインを上る
第１７章：代数を少々
第１８章：数論と量子力学の出会い
第１９章：黄金の鍵を回す
第２０章：リーマン演算子とその他のアプローチ
第２１章：誤差項
第２２章：正しいかそうでないか、いずれかだ

エピローグ
付録　歌になったリーマン予想
註
訳者あとがき
索引

↧

声でつづる昭和人物史～湯川秀樹（NHKラジオ第２）

January 15, 2018, 6:41 am

≫ Next: Square root 501,264 using abacus (Half-multiplication table method 7)

≪ Previous: 素数に憑かれた人たち～リーマン予想への挑戦～：ジョン・ダービーシャー

先週月曜から、物理学者の湯川秀樹博士の肉声が聞けるラジオ番組が放送されているので告知しておこう。

聴き逃した方は、「らじる★らじる」のホームページやスマホアプリのストリーミング再生や「聴き逃し」で聴いていただきたい。

らじる★らじる（NHKネットラジオ）

第１回と第２回を聴いてみたが、湯川博士の幼少期の意外な一面を知ることになった。

カルチャーラジオ NHKラジオアーカイブス
ラジオ第2 毎週月曜午後8時30分再放送毎週月曜午前10時
http://www4.nhk.or.jp/P1890/

放送終了分はここから聴けます：開く

「声でつづる昭和人物史～湯川秀樹」1
放送：1月8日（月）午後8時30分～午後9時00分
再放送：1月15日（月）午前10時0分～午前10時30分

「私の自叙伝・ある物理学者の宿命」（1）生い立ち（1962（昭和37）年6月15日放送）ノンフィクション作家・評論家…保阪正康,【司会】宇田川清江

「声でつづる昭和人物史」1月は4回にわたり湯川秀樹（1907～81）を取り上げます。湯川秀樹は1949年、日本人で初めてノーベル賞を受賞した人物としてその名が知られています。当時、物理学者で京都大学教授でした。第1回は、昭和37年（1962）6月15日に放送した「私の自叙伝・ある物理学者の宿命」を紹介します。学者の家に生まれ育ったその生い立ちや幼少期についてなどエピソードを交えながら語っています。

「声でつづる昭和人物史～湯川秀樹」2
放送：1月15日（月）午後8時30分～午後9時00分
再放送：1月22日（月）午前10時0分～午前10時30分

「私の自叙伝・ある物理学者の宿命」（2）学問への道（1962（昭和37）年6月15日放送）ノンフィクション作家・評論家…保阪正康,【司会】宇田川清江

「声でつづる昭和人物史～湯川秀樹」。第2回は昭和37年（1962）6月15日に放送した「私の自叙伝・ある物理学者の宿命」から、中学校や高等学校時代の思い出、そして京都大学で物理学を志すに至ったいきさつなどについて語っています。

「声でつづる昭和人物史～湯川秀樹」3
放送：1月22日（月）午後8時30分～午後9時00分
再放送：1月29日（月）午前10時0分～午前10時30分

「私の自叙伝・ある物理学者の宿命」（3）物理学者として（1962（昭和37）年6月15日放送）ノンフィクション作家・評論家…保阪正康,【司会】宇田川清江

「声でつづる昭和人物史～湯川秀樹」。第3回は昭和37年（1962）6月15日に放送した「私の自叙伝・ある物理学者の宿命」から紹介します。湯川秀樹は、物理学者として海外の学者とも積極的に交流し研究を続けその成果が認められ1949年にノーベル賞を受賞します。しかし、戦後は「原子力」「核」の時代となり学問の世界にだけ閉じこもっていくことが出来なくなり行動をおこすに至ります。その経緯を語ります。

「声でつづる昭和人物史～湯川秀樹」4
放送：1月29日（月）午後8時30分～午後9時00分
再放送：2月5日（月）午前10時0分～午前10時30分

「人類と原子力」（1955（昭和30）年1月2日放送）ノンフィクション作家・評論家…保阪正康,【司会】宇田川清江

「声でつづる昭和人物史～湯川秀樹」。第4回は昭和30年（1955）1月2日に放送された「人類と原子力」を紹介します。前年の1954年3月に、ビキニ環礁でアメリカによる水爆実験があり、日本の船が被曝した「第五福竜丸事件」が起きています。現在に至るまで大きな課題となっている「原子力」や「核」の在り方について、湯川博士がその思いを語っています。

ブログ執筆のはげみになりますので、１つずつ応援クリックをお願いします。

↧

Square root 501,264 using abacus (Half-multiplication table method 7)

January 17, 2018, 12:54 am

≫ Next: 開平と開立（第37回）：501,264の算盤による開平（半九九法7）

≪ Previous: 声でつづる昭和人物史～湯川秀樹（NHKラジオ第２）

[Set 501,264 on Mr. Square root]Zoom

[Japanese]

We will continue from where we ended in the last article, the actual solutions to calculate Square root using abacus. Today's example is Half-multiplication table method (Hankuku method), root is 3-digits case and contains Zero. Please check the Theory page for your reference. You can check the Index page of all articles.

Square root methods: Double-root method, Double-root alternative method, half-multiplication table method, half-multiplication table alternative method, multiplication-subtraction method, constant number method, etc.

Abacus steps to solve Square root of 501,264
(Answer is 708)

"1st group number" is the left most numbers in the 2-digits groups of the given number for square root calculation. Number of groups is the number of digits of the Square root.

501,264 -> (50|12|64) : 50 is the 1st group number. The root digits is 2.

Step 1: Place 501264 on CDEFGH.

Step 2: The 1st group is 50.

Step 3: Square number ≦ 50 is 49=7^2. Place 7 on B as the 1st root.

Step 4: Subtract 7^2 from the 1st group 50. Place 50-7^2=01 on CD.

Step 5: Focus on 11264 on DEFGH.

Step 6: Divide 11264 by 2. Place 11264/2=05632 on DEFGH.

Step 7: Divide 05 on DE by the current root 7.

Step 8: Cannot divide. Place 0 on C as 2nd root.

Step 9: Divide 563 on EFG by the current root 70. 563/70=8 remainder 3

Step 10: Place 8 on D as 3rd root.

Step 11: Place remainder 003 on EFG.

Step 12: Focus on 32 on GH.

Step 13: Subtract 3rd root^2/2 from 32 on GH. Place 00 on GH.

Step 14: Square root of 501264 is 708.

Final state: Answer 708

Abacus state transition. (Click to Zoom)

From next article, we start examples of cube root calculation using 1/3-multiplication table method.

Related articles:

How to solve Cube root of 1729.03 using abacus? (Feynman v.s. Abacus man)
http://blog.goo.ne.jp/ktonegaw/e/cff5d6e7ecaa07230b9cc7af10b23aed

Index: Square root and Cube root using Abacus
http://blog.goo.ne.jp/ktonegaw/e/f62fb31b6a3a0417ec5d33591249451b

Please place your mouse on the buttons and click one by one. These are blog ranking sites.

↧

開平と開立（第37回）：501,264の算盤による開平（半九九法7）

January 17, 2018, 12:57 am

≫ Next: Square root 11,943,936 using abacus (Half-multiplication table method 8)

≪ Previous: Square root 501,264 using abacus (Half-multiplication table method 7)

「開平はん」に501,264を置いたところ拡大

[English]

前回に続き、算盤での開平の手順を解説する。今回も半九九法で、根が３桁で根に0が含まれるケース。理論編も参考にしていただきたい。全体の目次はこのページを開くと見ることができる。

開平（平方根）：倍根法(2商法)、倍根法別法、半九九法、半九九法別法、乗減法、定数法(折衷法) 、過大数開平、省略開平など

算盤による501,264の2乗根の解法（答は708）

第１群の数とは平方根を求める数を２桁ずつ区切り、いちばん大きい（いちばん左）の２桁のことである。群の数が根の桁数となる。

501,264 -> (50|12|64) : 50が第１群の数、根の桁数は3

手順 1: 501264をCDEFGHに置く。

手順 2: 第1群は50。

手順 3: 50以下の平方数は49=7x7。7を初根としてBに立てる。

手順 4: 50-7^2=01をCDに置く。

手順 5: DEFGHの11264に注目する。

手順 6: 11264を二分する。すなわち11264/2=05632をDEFGHに置く。

手順 7: DEの05を既根7で割る。

手順 8: 商が立たないので次根を0としてCに置く。

手順 9: 563を既根70で割る。563/70=8余り3

手順 10: 商8を第3根としてDに置く。

手順 11: 余り003をEFGに置く。

手順 12: GHの32に注目する。

手順 13: GHの32から第3根^2/2を引く。32-8^2/2=00をGHに置く。

手順 14: 平方根は708と求まる。

最終状態：答 708

珠の状態推移を表にすると次のようになる。（クリックで拡大）

次回から三分九九法による開立の例を取り上げる。

関連記事：

ファインマン v.s. 算盤の達人：ファインマン先生に立方根計算の雪辱を果たそう
http://blog.goo.ne.jp/ktonegaw/e/89a0b907577f03ef6132cf9664bdcddb

目次：算盤による平方根、立方根の計算（開平、開立）
http://blog.goo.ne.jp/ktonegaw/e/bb0449f357398a2c24026f33af7f70ee

ブログ執筆のはげみになりますので、１つずつ応援クリックをお願いします。

↧

Square root 11,943,936 using abacus (Half-multiplication table method 8)

January 19, 2018, 12:56 am

≫ Next: 開平と開立（第38回）：1,1943,936の算盤による開平（半九九法8）

≪ Previous: 開平と開立（第37回）：501,264の算盤による開平（半九九法7）

[Set 11,943,936 on Mr. Square root]Zoom

[Japanese]

We will continue from where we ended in the last article, the actual solutions to calculate Square root using abacus. Today's example is Half-multiplication table method (Hankuku method), root is 4-digits case. Please check the Theory page for your reference. You can check the Index page of all articles.

Square root methods: Double-root method, Double-root alternative method, half-multiplication table method, half-multiplication table alternative method, multiplication-subtraction method, constant number method, etc.

Abacus steps to solve Square root of 11,943,936
(Answer is 3,456)

"1st group number" is the left most numbers in the 2-digits groups of the given number for square root calculation. Number of groups is the number of digits of the Square root.

11,943,936 -> (11|94|39|36) : 50 is the 1st group number. The root digits is 4.

Step 1: Place 11943936 on CDEFGHIJ.

Step 2: The 1st group is 11.

Step 3: Square number ≦ 11 is 3=3^2. Place 3 on B as the 1st root.

Step 4: Subtract 3^2 from the 1st group 11. Place 11-3^2=02 on CD.

Step 5: Focus on 2943936 on DEFGHIJ.

Step 6: Divide 2943936 by 2. Place 2943936/2=1471968 on DEFGHIJ.

Step 7: Divide 14 on DE by the current root 3.

Step 8: 14/3=4 remainder 2. Place 4 on C as 2nd root.

Step 9: Place remainder 02 on DE.

Step 10: Focus on 27 on EF.

Step 11: Subtract 2nd root^2/2 from 27 on EF. Place 27-4^2=19 on EF.

Step 12: Focus on 191 on EFG.

Step 13: Divide 191 on EFG by the current root 34. 191/34=5 remainder 1.

Step 14: Place 5 on D as 3rd root.

Step 15: Place remainder 021 on EFG.

Step 16: Focus on 19.6 on GHI.

Step 17: Subtract 3rd root^2/2 from 19.6 on GHI. Place 021 on GHI.

Step 18: Divide 2071 on FGHI by the current root 345. 2071/345=6 remainder 1.

Step 19: Place 6 on E as 4th root.

Step 20: Place remainder 0001 on FGHI.

Step 21: Focus on 18 on IJ.

Step 22: Subtract 3rd root^2/2 from 18 on IJ. Place 00 on IJ.

Step 23: Square root of 11943936 is 3456.

Final state: Answer 3456

Abacus state transition. (Click to Zoom)

It is interesting to compare with the Double-root method.

Next article is solving Cube root by 1/3-multiplication table method.

Related articles:

How to solve Cube root of 1729.03 using abacus? (Feynman v.s. Abacus man)
http://blog.goo.ne.jp/ktonegaw/e/cff5d6e7ecaa07230b9cc7af10b23aed

Index: Square root and Cube root using Abacus
http://blog.goo.ne.jp/ktonegaw/e/f62fb31b6a3a0417ec5d33591249451b

Square root 11,943,936 using abacus (Double-root method 9)
http://blog.goo.ne.jp/ktonegaw/e/55a2c0aead038f4f140a77798ce8ff47

Please place your mouse on the buttons and click one by one. These are blog ranking sites.

↧

開平と開立（第38回）：1,1943,936の算盤による開平（半九九法8）

January 19, 2018, 1:01 am

≫ Next: スタンダード佛和辞典・和佛辞典

≪ Previous: Square root 11,943,936 using abacus (Half-multiplication table method 8)

「開平はん」に1,1943,936を置いたところ拡大

[English]

前回に続き、算盤での開平の手順を解説する。今回も半九九法で、根が４桁のケース。理論編も参考にしていただきたい。全体の目次はこのページを開くと見ることができる。

開平（平方根）：倍根法(2商法)、倍根法別法、半九九法、半九九法別法、乗減法、定数法(折衷法) 、過大数開平、省略開平など

算盤による1,1943,936の2乗根の解法（答は3,456）

第１群の数とは平方根を求める数を２桁ずつ区切り、いちばん大きい（いちばん左）の２桁のことである。群の数が根の桁数となる。

1,1943,936 -> (11|94|39|36) : 11が第１群の数、根の桁数は4

手順1: 11943936をCDEFGHIJに置く。

手順2: 第1群は11。

手順3: 11以下の平方数は9=3x3。3を初根としてBに立てる。

手順4: 11-3^2=02をCDに置く。

手順5: DEFGHIJの2943936に注目する。

手順6: 2943936を二分する。すなわち2943936/2=1471968をDEFGHIJに置く。

手順7: DEの14を既根3で割る。14/3=4余り2

手順8: 商4を次根としてCに置く。

手順9: 余り02をDEに置く。

手順10: EFの27に注目する。

手順11: EFの27から次根^2/2を引く。27-4^2/2=19をEFに置く。

手順12: EFGの191に注目する。

手順13: EFGの191を既根34で割る。191/34=5余り21

手順14: 商5をDに置き、第3根とする。

手順15: 余り021をEFGに置く。

手順16: GHIの19.6に注目する。

手順17: GHIの19.6から第3根^2/2を引く。19.6-5^2/2=07.1をGHIに置く。

手順18: FGHIの2071を既根345で割る。2071/345=6余り1

手順19: 商6をEに置き、第4根とする。

手順20: 余り0001をFGHIに置く。

手順21: IJの18に注目する。

手順22: IJの18から第4根^2/2を引く。18-6^2/2=00をIJに置く。

手順23: 平方根は3456と求まる。

最終状態：答 3456

珠の状態推移を表にすると次のようになる。（クリックで拡大）

同じ問題の倍根法での解法と比べてみてほしい。

次回から三分九九法による開立の例をとりあげる。

関連記事：

ファインマン v.s. 算盤の達人：ファインマン先生に立方根計算の雪辱を果たそう
http://blog.goo.ne.jp/ktonegaw/e/89a0b907577f03ef6132cf9664bdcddb

目次：算盤による平方根、立方根の計算（開平、開立）
http://blog.goo.ne.jp/ktonegaw/e/bb0449f357398a2c24026f33af7f70ee

開平と開立（第15回）：11,943,936の算盤による開平（倍根法９）
http://blog.goo.ne.jp/ktonegaw/e/fd3ab9832afa2c280dfd0d0d70e0562f

ブログ執筆のはげみになりますので、１つずつ応援クリックをお願いします。

↧

スタンダード佛和辞典・和佛辞典

January 20, 2018, 3:53 am

≫ Next: ４年ぶりの大雪警報（東京）

≪ Previous: 開平と開立（第38回）：1,1943,936の算盤による開平（半九九法8）

拡大

今日の午後はフランス語の授業をして過ごした。前回「フランス語の辞書はどれがいい？」という記事で、お勧めの辞書を紹介させていただき、初学者はなるべく新しい辞書を使ったほうがよいことを述べた。

しかしフランス文学、特に古典文学を読み解くのであれば話は別である。現在では使われなくなった語義や用例が載っている辞書が必要になる。今日紹介する「スタンダード仏和辞典」、「スタンダード和仏辞典」がお勧めなのだ。

「スタンダード仏和辞典」と「スタンダード和仏辞典」は1985年に決定版の「ロワイヤル仏和中辞典（初版）」が刊行されるまで、いちばん使われた辞書である。仏和辞典は1957年に初版が、1974年に増補改訂版が刊行され、和仏辞典のほうは1970年に刊行され、同じ版が現在も販売されている。

1950年代から1980年代の仏和・和仏辞典を代表する本である。入手困難にならないうちにと革装のものを購入しておいた。革装のものはどちらも絶版だ。もしNHKの朝ドラ「ひよっこ」のみね子がフランス語を学んでいたとしたら、おそらくこの辞書を使っていたことだろう。

「スタンダード佛和辞典増補改訂版」(1974）
「スタンダード和佛辞典」(1970）

拡大

仏和辞典（拡大）

和仏辞典（拡大）

その後、仏和辞典のほうは改訂され1987年に「新スタンダード仏和辞典」が刊行された。こちらも古い語義や用例が載っている。中古本が苦手な方、新品が欲しい方は次の２冊をそろえるとよい。どちらもビニール装である。

「新スタンダード仏和辞典」(1987）
「スタンダード和佛辞典」(1970）

ところで1970年代に刊行された辞典には、興味深いことが書かれているのである。日本でフランス語の学習がどのように始まったか、どのような辞書が使われていたかということが序文に詳しく書かれているのだ。

昨年末、NHK BSプレミアムで『明治維新１５０年スペシャル「決戦！鳥羽伏見の戦い　日本の未来を決めた７日間」』という番組が放送された。この中で徳川幕府軍ではフランス語の号令が使われている。次のようなものだ。

気をつけ GARDE-A-VOUS ギャルダブ
右向け右 A droite DROITE アドロワットドロワット
回れ右 Demi-tour DROITE ドゥミトゥードロワット
右へならえ A droite alignement アドロワットアリニエモン
直れ FIXE フィックス
休め REPOS オーポー
前へ進め En avant MARCHE オンナヴァンマーシュ
駆け足進め Pas gymnastique MARCHE パジムナスティックマーシュ
中隊止まれ Compagnie HALTE コンパニーアルトゥ
小隊止まれ Section HALTE セクションアルトゥ
足踏み進め Marquez le pas MARCHE マッケルパマーシュ
担え銃 Portez ARME ポーテーアーム
捧げ銃 Présentez ARME プレザンテーアーム
直れ銃 Reposez ARME オポーゼーアーム
着剣 Baionnette au canon バヨネットオウカノン
取れ剣 Baionnette au fourreau バヨネットオウフロー
戦闘準備 Disposition de combat ディスポジションドゥコンバ
撃て FEU フー
撃方止め Halte au feuまたはCessez le feu アルトーフーまたはセッセルフー

徳川幕府軍でフランス語が使われていたのは、幕府がフランス式の軍事教練を導入していたからだ。フランス式軍事教練は後に明治新政府の陸軍に引き継がれることになる。（海軍にはオランダ語が導入されていた。）

陸軍と海軍の縄張り意識、対立はこの時代に生まれ、日清戦争では陸軍が、日露戦争では海軍が活躍することになる。そしてこの縄張り意識、対立はそのまま受け継がれ、後の太平洋戦争の敗因のひとつになった。

仏和辞典、和仏辞典のそれぞれの序文に、わが国におけるフランス語学習、辞書の歴史が詳しく書かれているので、ぜひお読みいただきたい。画像をクリックすると拡大する。スマートフォンによっては拡大画像が表示されないことがあるので、そのときは「ＰＣ表示」に切り替えてから画像クリックすると拡大画像が表示される。

「スタンダード佛和辞典増補改訂版」(1974）の序文

「スタンダード和佛辞典」(1970）の序文

関連記事：

フランス語の辞書はどれがいい？
http://blog.goo.ne.jp/ktonegaw/e/04d001a3857a63e9ec104903ccae1a83

フランス語を教え始めた
http://blog.goo.ne.jp/ktonegaw/e/da69b2a85fb8e10b225867d3fe2731da

ブログ執筆のはげみになりますので、１つずつ応援クリックをお願いします。

↧

４年ぶりの大雪警報（東京）

January 21, 2018, 11:30 pm

≫ Next: ひとまねこざるびょういんへいく

≪ Previous: スタンダード佛和辞典・和佛辞典

拡大

４年ぶりの大雪警報ということなので、記録として残しておこう。

写真は午後４時に撮影したもの。午後６時から９時の帰宅時間帯にピークをむかえるそうだ。写真はクリックで拡大するようにしておいた。

２年前に設置した日時計。（紹介記事）

気象情報によると23区の積雪量は３センチということだが、７センチくらいあるように見える。（積雪の経過）

「降雪量」と「積雪量」は違う？
https://www.excite.co.jp/News/bit/00091137390199.html

降雪と積雪の違いとは
https://weathernews.jp/s/topics/201711/290155/

帰宅時に交通機関の混乱が予想されます。みなさん気を付けて帰宅してください。

ブログ執筆のはげみになりますので、１つずつ応援クリックをお願いします。

↧