「楽しもう射影平面 目で見る組合せトポロジーと射影幾何学: 大田春外」(Kindle版)
内容紹介:
射影平面をキーワードとして、射影平面がキー・ポイントとなる「閉曲面の分類定理」と「デザルクの定理」を豊かな図とともに、ていねいに解説する。幾何学の美しさと楽しさが味わえる。
2016年7月刊行、213ページ。
著者について:
大田春外(おおたはると): 研究者情報: http://researchmap.jp/read0010844/
1950年生まれ。1973年鳥取大学教育学部を卒業。1976年大阪教育大学大学院教育学研究科修士課程修了。1979年筑波大学大学院数学研究科博士課程修了。現在、静岡大学名誉教授。理学博士。専門は集合論的トポロジー。
太田先生の著書: 書籍版を検索 Kindle版を検索
理数系書籍のレビュー記事は本書で347冊目。
本書はおよそ1年前、新宿の朝日カルチャーセンターで行われた「寺川奈津美の気象講座 秋の気象と台風」を受講した帰りにコクーンタワー地下の書店で買ったものだ。
好物は後にとっておくタイプだから、面白そうな本だと思いつつ、なかなか手を出さないでいた。
章立ては次のとおり。
第I部 目で見る閉曲面の分類定理
第1章 閉曲面とその表現
第2章 いろいろな曲面と閉曲面
第3章 多面体グラフとオイラー標数
第4章 閉曲面の分類定理
第II部 射影平面とデザルクの定理
第5章 平面上のデザルクの定理
第6章 射影平面の再構成
第7章 射影変換
第8章 複比
第I部は曲面のトポロジーと展開図を図示しながら表示式と呼ばれる数学表現との対応関係を楽しく学びながら射影平面についての感覚的理解を深め、閉曲面の分類定理を導く。
第II部ではユークリッド空間で成り立つ「デザルクの定理」とその双対定理を証明を含めて学び、その後、この定理が射影平面ではどうなるかを学ぶ。
射影平面は「平面」という言葉が使われているが、第I部では曲面として学び、第II部ではこれを座標付きの平面として扱う。射影平面上で成り立つ幾何学を射影幾何学と呼ぶ。
まず第I部からピックアップして紹介しよう。
曲面として皆さんにお馴染みなのは、球面、メビウスの輪、トーラス(ドーナツの表面)だろう。そしてトポロジーを少し学んだことがある人は「クラインの壺」もご存知だと思う。
クラインの壺
![]()
この図はクラインの壺が3次元ユークリッド空間に浮かんでいるように描いてあるが、「本来のクラインの壺」は4次元以上の空間にしか存在できない。無理して3次元空間の中に描いたから細い管のところが壺の本体と交叉してしまっている。4次元空間の中のクラインの壺ではこのような交叉が生じない。
次に紹介される「クロスキャップ」も4次元以上の空間にある曲面だ。3次元空間で無理して描くとこのような図形になる。鳥のくちばしの形のところが交叉しているが、4次元空間だと交叉しない。
![]()
クロスキャップの展開図はこのようなものだ。
![]()
展開図の形をトポロジー的に変形してクロスキャップを構成する手順はこのとおり。辺と辺を貼り付けるときは同じ文字どうしを矢印の向きも含めて一致するように行う。右下の(12)の状態でfとf、gとgを貼り合わせればクロスキャップが完成する。
拡大
![]()
クラインの壺、トーラス、メビウスの輪などについても、同じように展開図と構成方法が示される。
そして、本書のメインテーマの射影平面とはどのような形をしているのだろうか。射影平面も4次元空間に存在する曲面である。その展開図はこのとおり。
![]()
左の展開図をトポロジー的に曲げて円の形に変形させたのが右図であり、これも射影平面の展開図だ。どちらにしてもaとa、bとbを矢印の向きが一致するように貼り合わせるのは3次元空間では無理で、4次元空間でしか行うことができない。
曲面の交叉を許す形で射影平面を3次元空間に構成すると、このような形になるそうだ。これを「平面」と呼ぶのも不思議なものである。
![]()
どのように変形したら展開図からこのような形を構成できるのだろうか?そして射影平面はクラインの壺や球面と関わりをもっているそうだ。それは本書を読んでのお楽しみとしておこう。
本書ではさまざまな2次元の曲面の展開図と構成方法を視覚的に紹介しながら、それらの表示式を与えることで数学と図形の関係を解き明かしている。
第I部の締めは「閉曲面の分類定理」である。話をわかりやすくするために、本書では触れられていないが次元を1つ下げた「閉曲線の分類定理」を勝手にでっちあげて解説しよう。
1次元の形とは「線」であり一般的には曲線だ。トポロジー的に曲線が取りうる形は、次の2種類しかない。超弦理論で提唱される開弦(左)と閉弦(右)に対応している。
![]()
これは2次元以上であれば、どんなに高次元の空間であっても、この2種類しかないことはおわかりだろう。そして「閉曲線」に限れば輪ゴムの形(閉弦)の1種類しかない。だから分類するまでもないが、これが「閉曲線の分類定理」である。
同じ意味合いで2次元の曲面が取りうる形も種類が限られている。そして閉曲面に限れば、次の3種類しかないのだ。
![]()
nは「種数」と呼ばれ、曲面に空いた「穴」の数である。ちなみに円筒の側面やメビウスの輪は曲面ではあるが、縁(ふち)があるから「開曲面」と呼ばれ、この3種類には含まれない。(曲線の場合の縁は開いた弦の両端の2点である。)
(1)は射影平面の系列で4次元空間にある曲面
(2)はトーラス(ドーナツの表面)の系列で3次元空間にも埋め込み可能な曲面
(3)は球面であり、もちろん3次元空間に埋め込み可能な曲面
4次元、5次元、...と空間の次元が増えるにつれて曲面の種類が増えていくわけではない。どんなに高い次元であっても曲面はこの3種類に分類されてしまう。ひとつ次元を下げた曲線のケースを思い出していただければ理解していただけるだろう。
さらにひとつ次元を上げて「閉曲立体の分類定理」を考えることもできる。閉曲立体は8種類に分類されるのだ。どんなに高次元空間であっても、その中にある閉じた立体の形は、トポロジー的な意味で8種類しかないのである。
これは10年前に書いた「トポロジカル宇宙(完全版):根上生也著」という記事で紹介した「サーストンの幾何化予想」のことだ。
1982年にアメリカのサーストンという数学者が「サーストンの幾何化予想」というものすごいアイデアを打ち立てた。「三次元多様体は一様な幾何構造の断片に分解できるだろう」というもので、宇宙を構成する空間の断片がこの図で示されているような最大8種類の形に限られていることを示した。サーストンはこれを証明したわけではない。ともかく物理学のように実験や観察で検証したわけでもないのに、頭の中の数学だけで宇宙の形の8種類の可能な断片を導きだしたことは他の数学者にとっても大きな驚きであった。これらがその8種類の形である。(動画を見る)
![]()
サーストン幾何化予想が証明されたことで2003年、グリゴリー・ペレルマンにより、およそ100年にわたり未解決だった3次元ポアンカレ予想が証明されたのは有名な話である。
余談: ブログ読者のhirotaさんからご指摘いただいたのだが、この図のうち1つは間違っている。図の一番上のH×EはH(双曲面)が底空間でE(ユークリッド計量のトーラス)がファイバーのファイバーバンドルを表わしていて細い線がファイバー、太い部分が底空間を表わしていると推察できるが、図の中央のS×Eはどう見ても底空間がS(球面)になってない。
もちろん本書のレベルをはるかに超えるので、「サーストン幾何」は、本書でごくあっさり触れられているに過ぎない。
第II部は座標平面上での射影幾何学が解説される。
無限に伸びる平行線。ユークリッド幾何学では平行線は無限の彼方まで伸びても交わらない。
![]()
しかし「平行線は無限の彼方の1点で交わる」と考えることも可能だ。そして前方の無限の彼方で交わった点と、後方の無限の彼方で平行線が交わった点を同一(同じ点)と見なすと考えるのだ。さらにそのような無限遠の点は、自分の回りの360度すべての方向にある。自分を中心とした無限大の円を考え、円周上の無限遠点と円の中心に対して反対側の無限遠点を同一と見なすことにする。通常のユークリッド平面をこのように修正したものが「射影平面」である。
射影平面上の直線は次のように描かれる。無限遠のところにある円周は射影平面上では「直線」であることに注意していただきたい。
拡大
![]()
射影平面上の幾何の性質を探るために、ユークリッド空間で成り立っている「デザルクの定理」とその双対定理が射影平面上ではどのようになるかを本書では例として取り上げている。これは次の図のように空間内の二つの三角形の相互の関係に関する幾何の定理だ。
拡大
![]()
不思議なことにこの定理で「点」を「線」に読み替え、「線」を「点」に読み替えると、もうひとつ別の関係が成り立っているのである。これを双対定理と呼んでいる。対応する2つの定理の関係は次のようになる。
拡大
![]()
デザルクの定理の双対定理を図示すると、このようになる。ユークリッド幾何の世界だけでも、じゅうぶん興味深い。
拡大
![]()
さて、これらの定理を射影平面上に移すとどのようなことになるのか?定理は相変わらず成り立っているのか?それも本書を読んでのお楽しみということにしておこう。
そして第II部の後半では斜影平面に座標を導入し、射影変換と呼ばれる幾何的な座標変換を学ぶ。これはユークリッド空間では「1次変換」そして「平行移動」として学ぶ事がらだ。ユークリッド空間では「1次変換」と「平行移動」を合成した変換のことを「アフィン変換」と呼んでいる。特殊相対性理論に使われるローレンツ変換は4次元のアフィン変換である。
本書のこの部分は通常の線形代数を学んだ人には、とても興味深い内容だ。ぜひお読みいただきたい。
この紹介記事ではかいつまんで紹介したため、論理的な整合性が損なわれている。(たとえば「第3章 多面体グラフとオイラー標数」の解説は割愛した。)実際に本書で筋道をたどりながら読み進めると、射影幾何の世界は、私たちが慣れ親しんでいるユークリッド的な世界と同じ数学的実在感をもったパラレルワールドであることを理解していただけると思う。
特に第I部でいろいろな形を変形させたり、切ったり貼ったりする様子を見るのはとても楽しい。自分にはこんな図は描けないと思いながら、あれよあれよという間に奇妙な形が出来上がっていく。そして形の変形が表示式の代数操作と対応しているのを見ると、現代数学はこのようにして誕生したのだと納得できるのだ。
本書で射影平面に対する感覚を体得した方は、「射影幾何学」というキーワードで検索し、より専門的な教科書に進むとよいだろう。
射影幾何学の本: Amazonで検索
ところで先月から竹野内豊さんが結び目理論専攻数学者を演じるNHKドラマ10『この声をきみに』という番組が放送されている。この中に「3次元多様体と結び目(瀬川篤郎編、松谷書店)」というトポロジーの教科書が映されるのだが、調べてみたところこの本は実際には存在しない架空の本であることがわかった。
![]()
このドラマで竹野内さんは家族との生活の中で数学的妄想に熱中するあまり、ミムラさんが演じる妻に極度のストレスを与え、離婚の危機に瀕してしまう。「数学者=変人」というレッテルがストーリーのベースだ。
ドラマを見ながら「そろそろこのようなステレオタイプな見方はやめてほしいものだ」と思いつつ、自信をもってそう主張できないもう一人の自分がいることに気が付かされた。
関連記事:
はじめよう位相空間:大田春外
http://blog.goo.ne.jp/ktonegaw/e/98d355dcb790031607d752984929fe3d
解いてみよう位相空間:大田春外
http://blog.goo.ne.jp/ktonegaw/e/008e49c402513499938c41f8e7083d7a
ブログ執筆のはげみになりますので、1つずつ応援クリックをお願いします。
![にほんブログ村 科学ブログ 物理学へ]()
![人気ブログランキングへ]()
![]()
![]()
![]()
![]()
![]()
「楽しもう射影平面 目で見る組合せトポロジーと射影幾何学: 大田春外」(Kindle版)
![]()
第I部 目で見る閉曲面の分類定理
第1章 閉曲面とその表現
- 曲面と閉曲面
- 位相同型
- 球面とトーラス
- 閉曲面の展開図と表示式
第2章 いろいろな曲面と閉曲面
- 円板・アニュラス・メビウスの帯
- 球面・トーラス・クラインの壺
- 展開図と表示式の同値関係
- クロスキャップ
- 射影平面
- 曲面の向き付け可能性
第3章 多面体グラフとオイラー標数
- 多面体グラフ
- 閉曲面のオイラー標数
- 球面S^2の正多面体グラフ
-
第4章 閉曲面の分類定理
- 閉曲面の連結和
- 基本変形
- 閉曲面の分類定理
第II部 射影平面とデザルクの定理
第5章 平面上のデザルクの定理
- デザルクの定理のいろいろな形
- 空間におけるデザルクの定理
- 双対定理と逆
第6章 射影平面の再構成
- 射影平面の再構成
- 座標の導入と直線の方程式
- 点と直線に関する基本命題
- 射影平面上のデザルクの定理
第7章 射影変換
- 1次変換とアフィン変換
- 射影変換
- デザルクの定理の別証明
- 射影平面上のアフィン変換
第8章 複比
- 点列の複比
- 線束の複比と基本命題
- ハップスの定理とデザルクの定理
A:演習問題の解答例とヒント
参考書
索引
ギリシャ文字一覧表
内容紹介:
射影平面をキーワードとして、射影平面がキー・ポイントとなる「閉曲面の分類定理」と「デザルクの定理」を豊かな図とともに、ていねいに解説する。幾何学の美しさと楽しさが味わえる。
2016年7月刊行、213ページ。
著者について:
大田春外(おおたはると): 研究者情報: http://researchmap.jp/read0010844/
1950年生まれ。1973年鳥取大学教育学部を卒業。1976年大阪教育大学大学院教育学研究科修士課程修了。1979年筑波大学大学院数学研究科博士課程修了。現在、静岡大学名誉教授。理学博士。専門は集合論的トポロジー。
太田先生の著書: 書籍版を検索 Kindle版を検索
理数系書籍のレビュー記事は本書で347冊目。
本書はおよそ1年前、新宿の朝日カルチャーセンターで行われた「寺川奈津美の気象講座 秋の気象と台風」を受講した帰りにコクーンタワー地下の書店で買ったものだ。
好物は後にとっておくタイプだから、面白そうな本だと思いつつ、なかなか手を出さないでいた。
章立ては次のとおり。
第I部 目で見る閉曲面の分類定理
第1章 閉曲面とその表現
第2章 いろいろな曲面と閉曲面
第3章 多面体グラフとオイラー標数
第4章 閉曲面の分類定理
第II部 射影平面とデザルクの定理
第5章 平面上のデザルクの定理
第6章 射影平面の再構成
第7章 射影変換
第8章 複比
第I部は曲面のトポロジーと展開図を図示しながら表示式と呼ばれる数学表現との対応関係を楽しく学びながら射影平面についての感覚的理解を深め、閉曲面の分類定理を導く。
第II部ではユークリッド空間で成り立つ「デザルクの定理」とその双対定理を証明を含めて学び、その後、この定理が射影平面ではどうなるかを学ぶ。
射影平面は「平面」という言葉が使われているが、第I部では曲面として学び、第II部ではこれを座標付きの平面として扱う。射影平面上で成り立つ幾何学を射影幾何学と呼ぶ。
まず第I部からピックアップして紹介しよう。
曲面として皆さんにお馴染みなのは、球面、メビウスの輪、トーラス(ドーナツの表面)だろう。そしてトポロジーを少し学んだことがある人は「クラインの壺」もご存知だと思う。
クラインの壺

この図はクラインの壺が3次元ユークリッド空間に浮かんでいるように描いてあるが、「本来のクラインの壺」は4次元以上の空間にしか存在できない。無理して3次元空間の中に描いたから細い管のところが壺の本体と交叉してしまっている。4次元空間の中のクラインの壺ではこのような交叉が生じない。
次に紹介される「クロスキャップ」も4次元以上の空間にある曲面だ。3次元空間で無理して描くとこのような図形になる。鳥のくちばしの形のところが交叉しているが、4次元空間だと交叉しない。

クロスキャップの展開図はこのようなものだ。

展開図の形をトポロジー的に変形してクロスキャップを構成する手順はこのとおり。辺と辺を貼り付けるときは同じ文字どうしを矢印の向きも含めて一致するように行う。右下の(12)の状態でfとf、gとgを貼り合わせればクロスキャップが完成する。
拡大

クラインの壺、トーラス、メビウスの輪などについても、同じように展開図と構成方法が示される。
そして、本書のメインテーマの射影平面とはどのような形をしているのだろうか。射影平面も4次元空間に存在する曲面である。その展開図はこのとおり。
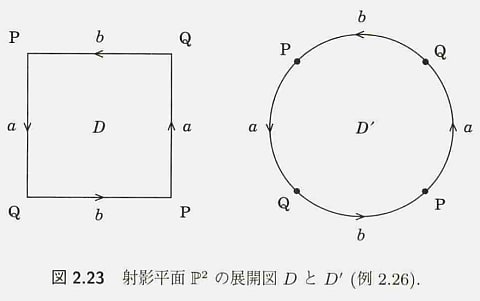
左の展開図をトポロジー的に曲げて円の形に変形させたのが右図であり、これも射影平面の展開図だ。どちらにしてもaとa、bとbを矢印の向きが一致するように貼り合わせるのは3次元空間では無理で、4次元空間でしか行うことができない。
曲面の交叉を許す形で射影平面を3次元空間に構成すると、このような形になるそうだ。これを「平面」と呼ぶのも不思議なものである。

どのように変形したら展開図からこのような形を構成できるのだろうか?そして射影平面はクラインの壺や球面と関わりをもっているそうだ。それは本書を読んでのお楽しみとしておこう。
本書ではさまざまな2次元の曲面の展開図と構成方法を視覚的に紹介しながら、それらの表示式を与えることで数学と図形の関係を解き明かしている。
第I部の締めは「閉曲面の分類定理」である。話をわかりやすくするために、本書では触れられていないが次元を1つ下げた「閉曲線の分類定理」を勝手にでっちあげて解説しよう。
1次元の形とは「線」であり一般的には曲線だ。トポロジー的に曲線が取りうる形は、次の2種類しかない。超弦理論で提唱される開弦(左)と閉弦(右)に対応している。

これは2次元以上であれば、どんなに高次元の空間であっても、この2種類しかないことはおわかりだろう。そして「閉曲線」に限れば輪ゴムの形(閉弦)の1種類しかない。だから分類するまでもないが、これが「閉曲線の分類定理」である。
同じ意味合いで2次元の曲面が取りうる形も種類が限られている。そして閉曲面に限れば、次の3種類しかないのだ。

nは「種数」と呼ばれ、曲面に空いた「穴」の数である。ちなみに円筒の側面やメビウスの輪は曲面ではあるが、縁(ふち)があるから「開曲面」と呼ばれ、この3種類には含まれない。(曲線の場合の縁は開いた弦の両端の2点である。)
(1)は射影平面の系列で4次元空間にある曲面
(2)はトーラス(ドーナツの表面)の系列で3次元空間にも埋め込み可能な曲面
(3)は球面であり、もちろん3次元空間に埋め込み可能な曲面
4次元、5次元、...と空間の次元が増えるにつれて曲面の種類が増えていくわけではない。どんなに高い次元であっても曲面はこの3種類に分類されてしまう。ひとつ次元を下げた曲線のケースを思い出していただければ理解していただけるだろう。
さらにひとつ次元を上げて「閉曲立体の分類定理」を考えることもできる。閉曲立体は8種類に分類されるのだ。どんなに高次元空間であっても、その中にある閉じた立体の形は、トポロジー的な意味で8種類しかないのである。
これは10年前に書いた「トポロジカル宇宙(完全版):根上生也著」という記事で紹介した「サーストンの幾何化予想」のことだ。
1982年にアメリカのサーストンという数学者が「サーストンの幾何化予想」というものすごいアイデアを打ち立てた。「三次元多様体は一様な幾何構造の断片に分解できるだろう」というもので、宇宙を構成する空間の断片がこの図で示されているような最大8種類の形に限られていることを示した。サーストンはこれを証明したわけではない。ともかく物理学のように実験や観察で検証したわけでもないのに、頭の中の数学だけで宇宙の形の8種類の可能な断片を導きだしたことは他の数学者にとっても大きな驚きであった。これらがその8種類の形である。(動画を見る)
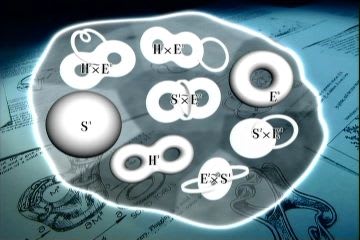
サーストン幾何化予想が証明されたことで2003年、グリゴリー・ペレルマンにより、およそ100年にわたり未解決だった3次元ポアンカレ予想が証明されたのは有名な話である。
余談: ブログ読者のhirotaさんからご指摘いただいたのだが、この図のうち1つは間違っている。図の一番上のH×EはH(双曲面)が底空間でE(ユークリッド計量のトーラス)がファイバーのファイバーバンドルを表わしていて細い線がファイバー、太い部分が底空間を表わしていると推察できるが、図の中央のS×Eはどう見ても底空間がS(球面)になってない。
もちろん本書のレベルをはるかに超えるので、「サーストン幾何」は、本書でごくあっさり触れられているに過ぎない。
第II部は座標平面上での射影幾何学が解説される。
無限に伸びる平行線。ユークリッド幾何学では平行線は無限の彼方まで伸びても交わらない。

しかし「平行線は無限の彼方の1点で交わる」と考えることも可能だ。そして前方の無限の彼方で交わった点と、後方の無限の彼方で平行線が交わった点を同一(同じ点)と見なすと考えるのだ。さらにそのような無限遠の点は、自分の回りの360度すべての方向にある。自分を中心とした無限大の円を考え、円周上の無限遠点と円の中心に対して反対側の無限遠点を同一と見なすことにする。通常のユークリッド平面をこのように修正したものが「射影平面」である。
射影平面上の直線は次のように描かれる。無限遠のところにある円周は射影平面上では「直線」であることに注意していただきたい。
拡大

射影平面上の幾何の性質を探るために、ユークリッド空間で成り立っている「デザルクの定理」とその双対定理が射影平面上ではどのようになるかを本書では例として取り上げている。これは次の図のように空間内の二つの三角形の相互の関係に関する幾何の定理だ。
拡大
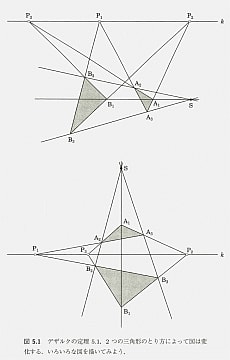
不思議なことにこの定理で「点」を「線」に読み替え、「線」を「点」に読み替えると、もうひとつ別の関係が成り立っているのである。これを双対定理と呼んでいる。対応する2つの定理の関係は次のようになる。
拡大

デザルクの定理の双対定理を図示すると、このようになる。ユークリッド幾何の世界だけでも、じゅうぶん興味深い。
拡大
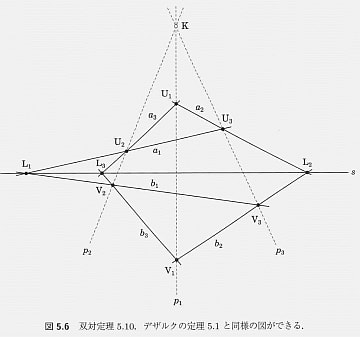
さて、これらの定理を射影平面上に移すとどのようなことになるのか?定理は相変わらず成り立っているのか?それも本書を読んでのお楽しみということにしておこう。
そして第II部の後半では斜影平面に座標を導入し、射影変換と呼ばれる幾何的な座標変換を学ぶ。これはユークリッド空間では「1次変換」そして「平行移動」として学ぶ事がらだ。ユークリッド空間では「1次変換」と「平行移動」を合成した変換のことを「アフィン変換」と呼んでいる。特殊相対性理論に使われるローレンツ変換は4次元のアフィン変換である。
本書のこの部分は通常の線形代数を学んだ人には、とても興味深い内容だ。ぜひお読みいただきたい。
この紹介記事ではかいつまんで紹介したため、論理的な整合性が損なわれている。(たとえば「第3章 多面体グラフとオイラー標数」の解説は割愛した。)実際に本書で筋道をたどりながら読み進めると、射影幾何の世界は、私たちが慣れ親しんでいるユークリッド的な世界と同じ数学的実在感をもったパラレルワールドであることを理解していただけると思う。
特に第I部でいろいろな形を変形させたり、切ったり貼ったりする様子を見るのはとても楽しい。自分にはこんな図は描けないと思いながら、あれよあれよという間に奇妙な形が出来上がっていく。そして形の変形が表示式の代数操作と対応しているのを見ると、現代数学はこのようにして誕生したのだと納得できるのだ。
本書で射影平面に対する感覚を体得した方は、「射影幾何学」というキーワードで検索し、より専門的な教科書に進むとよいだろう。
射影幾何学の本: Amazonで検索
ところで先月から竹野内豊さんが結び目理論専攻数学者を演じるNHKドラマ10『この声をきみに』という番組が放送されている。この中に「3次元多様体と結び目(瀬川篤郎編、松谷書店)」というトポロジーの教科書が映されるのだが、調べてみたところこの本は実際には存在しない架空の本であることがわかった。

このドラマで竹野内さんは家族との生活の中で数学的妄想に熱中するあまり、ミムラさんが演じる妻に極度のストレスを与え、離婚の危機に瀕してしまう。「数学者=変人」というレッテルがストーリーのベースだ。
ドラマを見ながら「そろそろこのようなステレオタイプな見方はやめてほしいものだ」と思いつつ、自信をもってそう主張できないもう一人の自分がいることに気が付かされた。
関連記事:
はじめよう位相空間:大田春外
http://blog.goo.ne.jp/ktonegaw/e/98d355dcb790031607d752984929fe3d
解いてみよう位相空間:大田春外
http://blog.goo.ne.jp/ktonegaw/e/008e49c402513499938c41f8e7083d7a
ブログ執筆のはげみになりますので、1つずつ応援クリックをお願いします。







「楽しもう射影平面 目で見る組合せトポロジーと射影幾何学: 大田春外」(Kindle版)

第I部 目で見る閉曲面の分類定理
第1章 閉曲面とその表現
- 曲面と閉曲面
- 位相同型
- 球面とトーラス
- 閉曲面の展開図と表示式
第2章 いろいろな曲面と閉曲面
- 円板・アニュラス・メビウスの帯
- 球面・トーラス・クラインの壺
- 展開図と表示式の同値関係
- クロスキャップ
- 射影平面
- 曲面の向き付け可能性
第3章 多面体グラフとオイラー標数
- 多面体グラフ
- 閉曲面のオイラー標数
- 球面S^2の正多面体グラフ
-
第4章 閉曲面の分類定理
- 閉曲面の連結和
- 基本変形
- 閉曲面の分類定理
第II部 射影平面とデザルクの定理
第5章 平面上のデザルクの定理
- デザルクの定理のいろいろな形
- 空間におけるデザルクの定理
- 双対定理と逆
第6章 射影平面の再構成
- 射影平面の再構成
- 座標の導入と直線の方程式
- 点と直線に関する基本命題
- 射影平面上のデザルクの定理
第7章 射影変換
- 1次変換とアフィン変換
- 射影変換
- デザルクの定理の別証明
- 射影平面上のアフィン変換
第8章 複比
- 点列の複比
- 線束の複比と基本命題
- ハップスの定理とデザルクの定理
A:演習問題の解答例とヒント
参考書
索引
ギリシャ文字一覧表