「もし文豪たちが カップ焼きそばの作り方を書いたら」
内容:
もしも村上春樹がカップ焼きそばの容器にある「作り方」を書いたら――
ツイッターで発信され、ネット上で大拡散されたあのネタが、太宰治、三島由紀夫、夏目漱石といった文豪から、星野源、小沢健二らミュージシャンまで、100パターンの文体にパワーアップして書籍化されました。読めば爆笑必至の文体模倣100連発。
さらにイラストは、手塚治虫をはじめとした有名漫画家の模倣を得意とするマンガ家・田中圭一氏の描き下ろしです!
6月7日に発売されるこの本が、いま話題になっている。もとは何の気なくしてみたツイートなのだそうだが発想が面白い。こういう言葉遊びは大好きだ。住吉美紀さんがナビゲートするTOKYO FM「Blue Ocean」でも紹介されていた。
たとえば村上春樹風だとこうなるそうだ。
![]()
この他にも次のページでいろいろなパターンのが読める。
文豪による『カップ焼きそばの作り方』シリーズが秀逸すぎるw
https://matome.naver.jp/odai/2146401785375858501
「カップ焼きそばの作り方」で文体模写!歌手・公人編
https://twitter.com/i/moments/734996015296565249
面白そうなので「とね日記風」で作文してみた。
おいしい作り方(とね日記風)
カップ焼きそばを食べるのは久しぶりだ。毎晩しているウォーキングの意味がなくなるかなと思いつつ手を出してしまう。もちろんビッグサイズ。
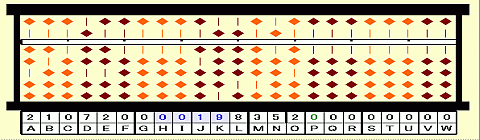
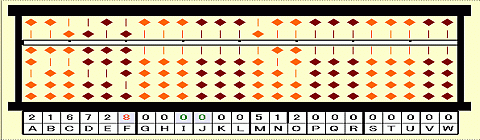
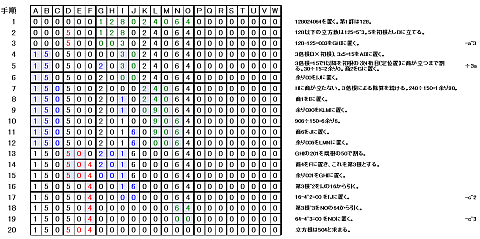
① 理数系の人なら包装もハサミで切るのだろう。でも僕はビリビリと手で破いてしまう。蓋を開けると麺の上にはソースと薬味のビニールパックが見える。どちらもお好みの分量使えばよいのだけど、ものぐさな僕は全部入れて、おまけに七味唐辛子をたっぷり加えるのだ。
② おっといけない!薬味とソースを先に入れてしまった。相変わらずのうっかり者である。「操作」には順番が大事だ。カップ焼きそばを作る手順は非可換なのだ。
③ 「覆水盆に返らず」とはやり直しがきかないということ。熱力学第2法則、不可逆過程である。こんなことがあるかもしれないと思って余分に買っておいたもうひとつでやり直し。失敗作はもったいないから後でどうするか考えよう。
④ 沸騰したお湯を注ぎこむ。やけどに注意だ。読みかけの本は脇へ寄せておこう。待っている間は失敗作の後始末。
⑤ 3分たったら湯きりである。あと少しで食べられるという高揚感、ワクワク感はお金では買うことのできない価値のひとつである。自分の幸せは自分で決める。カップ焼きそばは自分へのご褒美なのだ。
⑥ 湯が十分切れたところで薬味とソースを入れて麺に絡ませる。ソバやうどんは絡まないのにカップ焼きそばの麺はなぜ絡みやすいのか?今度書く記事のネタにしよう。(参考記事:「多次元空間へのお誘い(13):蕎麦やうどんの話」)
⑦ カップ焼きそばは今、とても売れているそうだ。アマゾンでは12個入りのがボックスで買える。ぜひ、お買い求めいただきたい。(Amazonを検索)
本をお求めの方は、こちらからどうぞ。
「もし文豪たちが カップ焼きそばの作り方を書いたら」
![]()
ブログ執筆のはげみになりますので、1つずつ応援クリックをお願いします。
![にほんブログ村 科学ブログ 物理学へ]()
![人気ブログランキングへ]()
![]()
![]()
![]()
![]()
![]()
内容:
もしも村上春樹がカップ焼きそばの容器にある「作り方」を書いたら――
ツイッターで発信され、ネット上で大拡散されたあのネタが、太宰治、三島由紀夫、夏目漱石といった文豪から、星野源、小沢健二らミュージシャンまで、100パターンの文体にパワーアップして書籍化されました。読めば爆笑必至の文体模倣100連発。
さらにイラストは、手塚治虫をはじめとした有名漫画家の模倣を得意とするマンガ家・田中圭一氏の描き下ろしです!
6月7日に発売されるこの本が、いま話題になっている。もとは何の気なくしてみたツイートなのだそうだが発想が面白い。こういう言葉遊びは大好きだ。住吉美紀さんがナビゲートするTOKYO FM「Blue Ocean」でも紹介されていた。
たとえば村上春樹風だとこうなるそうだ。

この他にも次のページでいろいろなパターンのが読める。
文豪による『カップ焼きそばの作り方』シリーズが秀逸すぎるw
https://matome.naver.jp/odai/2146401785375858501
「カップ焼きそばの作り方」で文体模写!歌手・公人編
https://twitter.com/i/moments/734996015296565249
面白そうなので「とね日記風」で作文してみた。
おいしい作り方(とね日記風)
カップ焼きそばを食べるのは久しぶりだ。毎晩しているウォーキングの意味がなくなるかなと思いつつ手を出してしまう。もちろんビッグサイズ。
① 理数系の人なら包装もハサミで切るのだろう。でも僕はビリビリと手で破いてしまう。蓋を開けると麺の上にはソースと薬味のビニールパックが見える。どちらもお好みの分量使えばよいのだけど、ものぐさな僕は全部入れて、おまけに七味唐辛子をたっぷり加えるのだ。
② おっといけない!薬味とソースを先に入れてしまった。相変わらずのうっかり者である。「操作」には順番が大事だ。カップ焼きそばを作る手順は非可換なのだ。
③ 「覆水盆に返らず」とはやり直しがきかないということ。熱力学第2法則、不可逆過程である。こんなことがあるかもしれないと思って余分に買っておいたもうひとつでやり直し。失敗作はもったいないから後でどうするか考えよう。
④ 沸騰したお湯を注ぎこむ。やけどに注意だ。読みかけの本は脇へ寄せておこう。待っている間は失敗作の後始末。
⑤ 3分たったら湯きりである。あと少しで食べられるという高揚感、ワクワク感はお金では買うことのできない価値のひとつである。自分の幸せは自分で決める。カップ焼きそばは自分へのご褒美なのだ。
⑥ 湯が十分切れたところで薬味とソースを入れて麺に絡ませる。ソバやうどんは絡まないのにカップ焼きそばの麺はなぜ絡みやすいのか?今度書く記事のネタにしよう。(参考記事:「多次元空間へのお誘い(13):蕎麦やうどんの話」)
⑦ カップ焼きそばは今、とても売れているそうだ。アマゾンでは12個入りのがボックスで買える。ぜひ、お買い求めいただきたい。(Amazonを検索)
本をお求めの方は、こちらからどうぞ。
「もし文豪たちが カップ焼きそばの作り方を書いたら」

ブログ執筆のはげみになりますので、1つずつ応援クリックをお願いします。