開平と開立（第10回）：4,761の算盤による開平（倍根法４）

March 21, 2017, 7:04 am

≪ Previous: Square root 4,761 using abacus (Double-root method 4)

「開平はん」に4,761を置いたところ拡大

[English]

前回に続き、算盤での開平の手順を解説する。今回も倍根法で、根が２桁、途中で9を立根する場合だ。理論編も参考にしていただきたい。

開平（平方根）：倍根法(2商法)、倍根法別法、半九九法、半九九法別法、乗減法、定数法(折衷法) 、過大数開平、省略開平など

算盤による4,761の2乗根の解法（答は69）

第１群の数とは平方根を求める数を２桁ずつ区切り、いちばん大きい（いちばん左）の２桁のことである。群の数が根の桁数となる。

4761 -> (47|61) : 47が第１群の数、根の桁数は2

手順１：4761を置く。第1群は7。

手順２：47以下の平方数は36=6x6。6を初根としてCに立てる。初根6の2倍の12をABに置き、倍根とする。

手順３：6の平方を第1群の47から引く。47-36=11となる。： -a^2

手順４：116に注目し、12で割る。

手順５：商9を得て、割止め、この商を次根とする。： ÷2a、116-9x12=008をEFGに置く。

手順６：9の平方=81を第2群の81から引く。： -b^2

手順７：根は69と求まる。

最終状態：答 69

珠の状態推移を表にすると次のようになる。（クリックで拡大）

第１１回も引き続き倍根法による開平を行う。

関連記事：

ファインマン v.s. 算盤の達人：ファインマン先生に立方根計算の雪辱を果たそう
http://blog.goo.ne.jp/ktonegaw/e/89a0b907577f03ef6132cf9664bdcddb

ブログ執筆のはげみになりますので、１つずつ応援クリックをお願いします。

とね日記は長年放置されている科学ブログランキングの不正クリックに対し、次のランキングサイトには適切な運営を期待します。
「FC2自然科学ブログランキング」：不正の例１例２（クリックしてからTwitterアプリで開くと画像は鮮明に見れます。）
（不正クリックブログの見分け方）

↧

発売情報：多様体入門(新装版) ：松島与三

March 21, 2017, 8:09 am

≫ Next: 正確な時計に影響を受け、周囲の時計が不正確になることを解明 - ウィーン大

≪ Previous: 開平と開立（第10回）：4,761の算盤による開平（倍根法４）

「多様体入門(新装版) ：松島与三」 - 詳細目次

内容紹介：
多様体は“空間”の概念を近代数学の立場から定式化したものであり、幾何学においてその根底をなすだけにとどまらず、理論物理学の大局的理解にも必要なものである。本書の旧版(初版1965年)は、長年にわたって多くの読者から親しまれ、英語版も刊行された本格的入門書である。
その旧版をもとに、2017年刊行の新装版では、最新の組版技術によって新たに本文を組み直し、レイアウトも刷新して読者の便宜を図った。なお改版にあたっては原則、一部の文字遣いを改めるにとどめ、本文は変更していない。
2017年4月7日刊行、294ページ。

著者について：
松島与三（まつしまよぞう）：ウィキペディア
1921年大阪府に生まれる。旧制浪速高等学校を経て、大阪大学理学部卒業。名古屋大学教授、大阪大学教授などを歴任。理学博士。1962年度朝日賞受章。

言わずもがなの多様体の名著である。1965年の刊行以来、どれほど多くの人がこの本の古くて読みにくい活字の本を我慢して学んだことだろう。

この教科書を使って「2016/自主ゼミ/松島多様体」も行われていたようだ。正誤表もこのページに置かれている。

「多様体入門(数学選書 (5))：松島与三」- 1965年版

まさに朗報である。来月ようやく読みやすい本が出ることになった。入門書というわりには手ごわい教科書だが、じっくり取り組んでほしい。多様体は大学では選択科目として３年生あるいは４年生で学ぶ。（参考：「大学で学ぶ数学とは（概要編）」）

もう少し易しめのをということならば「多様体 (共立数学講座) ：村上信吾」、さらに易しいのをご所望の方は「多様体の基礎 (基礎数学5) ：松本幸夫」をお求めになるとよいだろう。ただし、易しくなるにつれて説明が詳しく丁寧になるのだから、カバーしている項目が少なくなることに注意していただきたい。目次で比較してみるとよいだろう。

また1963年に刊行された名著「ルベーグ積分入門 (数学選書 (4))：伊藤清三」も最新の組版で同じタイミングで刊行されるそうだ。こちらも合わせてどうぞ。

「ルベーグ積分入門(新装版)：伊藤清三」- 詳細目次

「線型代数学(新装版)：佐武一郎」も最新の組版で刊行されたわけだし、「裳華房の数学選書」シリーズは順に新しくよみがえっていくことが期待される。

関連記事：

現代数学への招待:多様体とは何か:志賀浩二
http://blog.goo.ne.jp/ktonegaw/e/7aade4e043ef0b93de491bf674c734f3

多様体の基礎: 松本幸夫著
http://blog.goo.ne.jp/ktonegaw/e/a372a9ed92d55474cdbbb707922dc353

幾何学〈1〉多様体入門：坪井俊
http://blog.goo.ne.jp/ktonegaw/e/b3e1ce8cb8a308649bdf0db23a75e29b

ルベーグ積分入門：伊藤清三
http://blog.goo.ne.jp/ktonegaw/e/686a82d413fe6668cb776488820b1b39

大学で学ぶ数学とは（概要編）
http://blog.goo.ne.jp/ktonegaw/e/07137c47d16d95ddde8f5c4cb6f37d55

ブログ執筆のはげみになりますので、１つずつ応援クリックをお願いします。

「多様体入門(新装版) ：松島与三」

序言
読者のために

1．序論
　1.1　位相空間
　1.2　ベクトル空間
　1.3　n 次元数空間R^n とC^r 級関数
　1.4　逆関数の定理

2．可微分多様体
　2.1　多様体の定義
　2.2　可微分多様体の例
　2.3　可微分関数と局所座標系
　　　付記　可微分構造の従属性と同値性
　2.4　可微分写像
　2.5　接ベクトルと接ベクトル空間，リーマン計量
　2.6　関数の微分と臨界点
　2.7　写像の微分
　2.8　Sardの定理
　2.9　リーマン多様体の運動
　2.10　多様体の挿入とうめ込み，部分多様体
　2.11　ベクトル場と微分作用素
　2.12　ベクトル場と１パラメーター変換群
　2.13　リーマン多様体の無限小運動
　2.14　パラコンパクト多様体と単位の分割
　2.15　多様体の位相に関する種々の注意
　2.16　複素多様体
　2.17　概複素構造

3．微分形式とテンソル場
　3.1　p 次線型形式
　3.2　対称テンソルと交代テンソル，外積
　　　付記　対称積と対称多元環
　3.3　多様体上の共変テンソル場と微分形式
　3.4　テンソル場のリイ微分と微分形式の外微分
　3.5　写像による共変テンソル場の変換
　3.6　多様体のコホモロジー環
　3.7　複素多様体上の複素微分形式
　3.8　微分式系と積分多様体
　3.9　積分可能な概複素構造への応用
　3.10　極大連結積分多様体

4．リイ群と等質空間
　4.1　位相群
　4.2　位相群の部分群と商空間
　4.3　位相群の同型と準同型
　4.4　位相群の連結成分
　4.5　位相群の等質空間，局所コンパクト群
　4.6　リイ群とリイ環
　4.7　リイ群上の不変微分形式
　4.8　１パラメーター部分群と指数写像
　4.9　リイ群の例
　4.10　リイ群の標準座標系
　4.11　複素リイ群と複素リイ環
　4.12　リイ群のリイ部分群
　4.13　線型リイ群
　4.14　リイ群の商空間および商群
　4.15　リイ群の同型と準同型，リイ群の表現
　4.16　連結可換リイ群の構造
　4.17　１パラメーター部分群の微分可能性
　4.18　局所コンパクト群がリイ群になるための条件
　4.19　リイ変換群とリイ群の等質空間
　4.20　等質空間の例

5．微分形式の積分とその応用
　5.1　多様体の向きづけ
　5.2　微分形式の積分
　5.3　リイ群上の不変積分
　5.4　不変積分の応用
　5.5　ストークスの定理
　5.6　写像度
　5.7　ベクトル場の発散，ラプラシアン

あとがき
索引

↧

正確な時計に影響を受け、周囲の時計が不正確になることを解明 - ウィーン大

March 22, 2017, 7:10 am

≫ Next: クラウド量子計算入門：中山茂：(2) ブログ記事の方針変更

≪ Previous: 発売情報：多様体入門(新装版) ：松島与三

ウィーン大学とオーストリア科学アカデミーは、量子力学の対象となるミクロの世界において、ある時計の時刻を正確にすることによって、周囲の時計がその影響を受け、不正確になる効果があることを解明した。これは量子力学と一般相対性理論から導かれる根本的な効果であり、時間測定の物理的限界を示すものであるという。研究論文は、「米国科学アカデミー紀要（PNAS）」に掲載された。（マイナビニュースの元記事）

つい先日の筑波大学による「時間結晶の室温観測に成功」に続き、またもや奇怪な科学ニュースが飛び込んできた。

にわかには信じられない今回のニュース。後日確認しやすいように記事として残しておこう。（本業の仕事に忙殺されていて、じっくり論文を読む時間がとれない。どなたか専門の先生がわかりやすく解説してくださらないかなと思うわけである。）

とりあえずマイナビニュースの説明の中に「ん、これは正しいの？」というところを見つけた。

「まず、ある時計の時刻を正確に測定すればするほど、その時計のもつエネルギーの不確定性は増大する。」

時刻を正確に測定することを時計のエネルギーの不確定さに結び付けてよいの？？

僕が理解している時間とエネルギーの不確定性原理とは、たとえば「素粒子どうしの衝突時刻を正確に測定すれば、その衝突で発生するエネルギーが不確定になる。」あるいは「素粒子どうしの衝突で発生するエネルギーを正確に測定すれば衝突時刻が不確定になる。」というものだ。上の説明の「時計のもつエネルギー」とは結びつかない気がする。

時刻の測定をするなら、何らかの物理現象があっての測定であるべきで、ただ「時計の時刻を正確に測定する」という説明が何を意味しているのかわからない。もうひとつ別の時計を使って測定対象の時計の針が何かの数字を示す時刻を測定して１つめの時計が正確なことを確認するということ？？

それはそれでおかしなことだ。量子力学の観測問題と同様、２つめの時計の正確さを測るために３つめの時計が必要になり、３つめの時計の正確さを図るために４つ、５つ...、時計は無限個必要になるからだ。

このニュースを気持ち悪く感じるのは、このようなところにある。

そして、もうひとつよくわからないのは次の部分である。

「時計のエネルギーの不確定性が増大すればするほど、時間の遅れ度合い自体の不確定性もまた増大してしまう。」

という箇所は特殊相対論（E=mc^2：エネルギーと質量は等価）および一般相対論（重力理論：質量の周りでは時間は遅れる）からは納得できるけど本当なのかな？という気がする。

そもそも量子力学と一般相対論って矛盾しているわけだから、組み合わせて使ってよいのだろうか？でも「矛盾している」のは「重力子は繰り込み不可能（量子重力の紫外破綻＝繰り込み不可能性）」という理由だから、今回の話とは関係ないのかもしれないが。

最初の疑問について、つまり時間とエネルギーに不確定性原理が成り立つかどうかは堀田昌寛先生による次のページに書かれているように否定的な見解が示されている。

時間とエネルギーの不確定性関係と、相対性理論
http://mhotta.hatenablog.com/entry/2014/04/29/181417

またウィキペディアの「不確定性原理」の中の「時間とエネルギーの不確定性関係」にも次のように否定的な見解が示されている。

時間とエネルギーに関しては、観測量の分散に対するロバートソン不等式を論じることは一般にできない。それはエネルギー固有値が連続でかつ上限および下限を持たない量子系でなければ、ハミルトニアン H(hat) 正準共役な時間演算子 T(hat) は定義できないためである。

そして、谷村省吾先生はPDF文書で次のようにお書きになっている。

時間とエネルギーの不確定性関係 — 腑に落ちない関係（谷村省吾）
http://www2.yukawa.kyoto-u.ac.jp/~soken.editorial/sokendenshi/vol16/tanimura.pdf

時間幅とエネルギー幅の定量的関係を言うのは難しい。ロバートソンの不等式を適用できないのである。
相互作用が無限の過去から無限の未来まで続いていて，結合係数 g(t) が ∞ ＜ t ＜ ∞ にわたって定義されているなら、g(t) と G(E) が全実数上のフーリエ変換で関係づけられ、波束の不確定性関係と同形の時間とエネルギーの不確定性が成り立つ。

またこのページには証明付きで次のように書かれている。

「パウリの定理：ある量子系にハミルトニアン H(hat) と正準共役で、かつエルミートな時間演算子 T(hat) が存在する場合、ハミルトニアンの固有値は連続値で (-∞,+∞) の領域のすべての値をとる。」が成り立つならば時間とエネルギーの不確定性関係はあるわけです。
これはハミルトニアンが特別な性質を持たないと物理的時間演算子は存在しないということを意味しているわけです。

けれども、同じページには次のようにも書かれている。（時間とエネルギーの不確定性関係は条件付きで成り立つのだろうか？）

全状態空間内部ではエルミート演算子ではないが部分空間でエルミート演算子として振舞うものは、シンメトリック演算子を呼ばれており、シンメトリックな時間演算子の研究は数学の分野として今でも研究が盛んなようです。

それから何年か前の数理科学（？）という雑誌だったかと思いますが、電通大の長岡先生が量子推定の枠組みで厳密に証明できる時間とエネルギーの不確定性関係の不等式の話をされていたように思います。

「時間とエネルギーの不確定性」は大勢の物理学者、数学者が研究を重ねてきた問題だ。でも、それなりに根拠と自信があるからこのチームは論文を発表したのだろう。

時間とエネルギーの間に不確定性がないから、と切り捨ててしまうのは早計かもしれない。

公開されている論文はPDFだとAppendixを含めて12ページ。（うち本編は7ページ）ざっと見たところまるで歯が立たないというものではなさそうなので、時間があるときに読んでみたい。

Entanglement of quantum clocks through gravity
http://m.pnas.org/content/114/12/E2303

全文（HTML）
全文（PDF）

関連記事：

時：渡辺慧
http://blog.goo.ne.jp/ktonegaw/e/d149cf16bb9dd319f572e4228fdfe241

ハイゼンベルクの顕微鏡（不確定性原理は超えられるか）
http://blog.goo.ne.jp/ktonegaw/e/5597b85d83e795a22e97ca4d4ab97123

ブログ執筆のはげみになりますので、１つずつ応援クリックをお願いします。

↧

クラウド量子計算入門：中山茂：(2) ブログ記事の方針変更

March 24, 2017, 11:59 pm

≫ Next: 量子コンピュータ、量子アルゴリズムを学びたい高校生のために

≪ Previous: 正確な時計に影響を受け、周囲の時計が不正確になることを解明 - ウィーン大

「Ideal Quantum Processor」は量子コンピュータを古典コンピュータを使ってシミュレートするものである。これを選択するとComposerは次のような画面で表示されていた。

MEASUREというところに２つのアイコンがあることがおわかりになると思う。左は演算結果の量子ビットを測定するため、右はその測定をブロッホ球で表示するための測定のためのアイコンだ。そして、これら２つの測定アイコンは各量子ビットごと、複数配置することができる。量子ビット毎の測定結果を同じ画面で一度に表示させることができるわけだ。

そして測定結果のブロッホ球も、測定アイコンを配置した数だけ同じ画面で表示されるから、わかりやすいスクリーンショットを撮ることができる。

本書にも書かれているがComposerの選択画面で「Real Quantum Processor」を選択すると、配置できる測定アイコンはひとつだけなので、量子ビット毎に複数の測定アイコンを置くことができない。またブロッホ球測定のアイコンは現在の仕様では無くなってしまっている。

本書ではわかりやすいスクリーンショットを掲載するために、あえて「Ideal Quantum Proccessor」を選択しているのだと理解した。そして、現在はこの手法が使えないのである。

わかりやすく見せるためにスクリーンショットを加工して、複数の量子ビットを同じ画面に表示させると「嘘画面」を紹介することになるし、各量子ビット毎に画面を載せるのでは、記事はだらだらと長くなり、わかりづらい解説になってしまう。

理由の２つめは、現在の仕様で解説しているわかりやすいサイトやブログがあることに気が付いたことだ。僕が紹介したいことがすでに書かれているから、時間を割いて同じような記事を書く必要がなくなってしまった。特に最初のものはこのサービスを提供しているIBMの方による記事で3月17日に公開されたばかりだ。日本語版オフィシャルサイトといってよい。

読者のみなさんには、次のようなサイト、ブログでこのクラウドサービスの詳細を理解していただきたい。

IBM Quantum Computing で計算してみよう
https://www.ibm.com/developerworks/jp/cloud/library/cl-quantum-computing/

量子コンピュータと量子ゲートと私
http://qiita.com/eccyan/items/180fb909a55a59bb4e1b

主婦が始める量子コンピュータ
http://keropiyo3.hatenablog.com/

もちろん本書はこのクラウドサービスや量子ゲートや演算の詳細を具体的に学ぶのに良い本だと思う。いま第４章を読んでいるところだ。

ただし、上記３つのサイト、ブログは入門的なもので本書の第４章までの内容が中心である。第５章で解説される制御NOTゲート（CNOTゲート）を使うことで、はじめて量子ビットの「もつれ状態（EPR状態）」を作り出すことができ、量子コンピュータらしいアルゴリズムが実装可能になる。今後、これらのサイトに制御NOTゲートの使用例が追記されていくことを期待している。

英語のUser Guideのほうには、もちろん制御NOTゲートを使った「もつれ状態」、たとえば「ベル状態（説明１、説明２）の量子ゲート回路の構成の仕方が解説されている。

このようなわけでブログ記事のほうは方針変更させていただき、差し当たり全体を通読しながらこのサービスを試したうえで、後日感想記事を投稿させていただくことにする。

著者の中山先生は次の本も2年前にお書きになっている。目次を見ると本書の理論的側面を学べる本だということがわかる。合わせてお読みになるとよいだろう。

「量子アルゴリズム：中山茂」（目次）

量子コンピュータ関連の本： Amazonで検索

関連記事：

発売情報：クラウド量子計算入門：中山茂
http://blog.goo.ne.jp/ktonegaw/e/d360b69100fbe723c5b9410dbf3f5f4d

量子コンピュータ入門：宮野健次郎、古澤明
http://blog.goo.ne.jp/ktonegaw/e/ef75709187cf4b35a12f2d9fdf73a320

ファインマン計算機科学：ファインマン, A.ヘイ, R.アレン
http://blog.goo.ne.jp/ktonegaw/e/4f7f453019fd463ed2bfdeaa7b288d79

関連ページ：

IBMの量子コンピュータを使ってみた
http://kadora.hatenablog.com/entry/2016/09/10/230116

従来のPCの1億倍高速な量子コンピューターはどのような仕組みで動いて物理的限界を突破しているのかがわかるムービー
http://gigazine.net/news/20151210-quantum-computers-explained/

わかりやすい量子コンピュータ
http://matome.naver.jp/odai/2133630808407668301

「ITエンジニアのための量子コンピュータ入門」連載一覧
http://codezine.jp/article/corner/629

量子力学の反常識が創りだす量子コンピューティングの世界
?量子コンピュータの頭脳としての量子アルゴリズム?
http://www.kyoto-su.ac.jp/project/st/st14_03.html

米メリーランド大学、世界初となる「汎用計算可能量子コンピュータ」モジュールを開発
http://pc.watch.impress.co.jp/docs/news/1014034.html

関連動画：

量子論、量子テレポーテーション、量子コンピュータ

量子チェス（Quantum Chess）の解説動画（記事１記事２）

ホーキング教授と俳優ポール・ラッドが量子チェスで決闘（記事）

注意：量子チェスは量子コンピュータと直接の関係はありません。念のため。

ブログ執筆のはげみになりますので、１つずつ応援クリックをお願いします。

「クラウド量子計算入門―IBMの量子シミュレーションと量子コンピュータ：中山茂」

第1章　はじめてのIBMの5量子ビット実験
1.1　IBMの量子シミュレーションと量子コンピュータ実験
1.2　クラウド量子計算に期待されること
1.3　クラウド量子計算への歩み
1.4　はじめてのIBMのクラウド量子計算
1.5　はじめてのIBMの量子シミュレータ
1.6　はじめてのIBMの量子コンピュータ

第2章　パウリゲートの量子実験
2.1　パウリゲートとは
2.2　恒等ゲートとパウリゲートを使った量子シミュレータ実験

第3章　アダマールゲートの量子実験
3.1　アダマール変換とは
3.2　アダマール演算による量子シミュレータ実験

第4章　位相シフトゲートの量子実験
4.1　位相シフト演算とは
4.2　T深度による量子実験

第5章　制御NOTゲートの量子実験
5.1　制御NOTゲートと重ね合わせ状態
5.2　制御NOTゲートによるもつれ状態生成
5.3　制御NOTゲートにおけるパウリ演算子
5.4　制御NOTゲートによる交換ゲート
5.5　制御Uゲートの生成

第6章　トフォリゲートの量子実験
6.1　3量子ビットのもつれ状態
6.2　トフォリゲートの量子実験
6.3　フレッドキンゲートの量子実験

第7章　ドイチ・ジョザ問題の量子実験
7.1　ドイチ問題の量子実験
7.2　ドイチ・ジョザ問題の量子実験

第8章　ベルンシュタイン・ヴァジラニ問題の量子実験
8.1　関数f(x)=x・aの定数aを求めるベルンシュタイン・ヴァジラニ問題
8.2　n=1のベルンシュタイン・ヴァジラニ問題
8.3　n=2のベルンシュタイン・ヴァジラニ問題
8.4　n=3のベルンシュタイン・ヴァジラニ問題

第9章　サイモン問題の量子実験
9.1　サイモン問題とは
9.2　n=2のサイモン問題の量子実験

第10章　量子フーリエ変換の量子実験
10.1　量子フーリエ変換の定義
10.2　量子フーリエ変換に必要な制御Sゲートの作成
10.3　量子フーリエ変換ゲートの実装
10.4　逆量子フーリエ変換ゲート
10.5　量子フーリエ変換によるシフト不変性

第11章　位相・固有値・位数推定問題の量子実験
11.1　位相推定問題の量子実験
11.2　ユニタリ変換の固有値推定アルゴリズムの量子実験
11.3　位数発見アルゴリズムの量子実験

第12章　ショアの素因数分解問題の量子実験
12.1　因数分解とユークリッドの互除法
12.2　ショアの素因数分解アルゴリズム
12.3　ショアの素因数分解のための量子回路

第13章　グローバーの探索問題の量子実験
13.1　グローバーの探索問題とは
13.2　グローバーの振幅増幅手法の量子回路

第14章　量子非局所性の量子実験
14.1　量子非局所性とCHSH不等式
14.2　GHZ状態の量子非局所性実験

第15章　量子通信の量子実験
15.1　量子高密度符号
15.2　量子転送

第16章　量子エラーとスタビライザー測定
16.1　量子エラーとシンドローム診断
16.2　ビットパリティ識別
16.3　符号パリティ識別

第17章　量子誤り訂正の量子実験
17.1　量子誤り訂正のための符号化と複合化
17.2　量子誤り訂正ゲート

↧

量子コンピュータ、量子アルゴリズムを学びたい高校生のために

March 27, 2017, 8:55 am

≫ Next: Square root 54,756 using abacus (Double-root method 5)

≪ Previous: クラウド量子計算入門：中山茂：(2) ブログ記事の方針変更

量子コンピュータの説明で使われている難しそうな数式
拡大

「クラウド量子計算入門：中山茂」の紹介記事を読んで、自分も「IBMの量子コンピュータ計算サービス」を使いながら量子コンピュータを学んでみたいと思っている方がいらっしゃると思う。

けれども説明には記事トップの画像のように、なにやら意味不明な数式ばかり書かれていて、これが理解できないと歯が立たないのだとあきらめてしまうわけだ。

そして量子力学が量子コンピュータの基礎理論だと聞き、数式を使わない入門書をひもといてもイメージがつかめるだけで、専門書のレベルにはほど遠いことがすぐわかる。

- では、数学IIIを学んだレベルの高校生はどうしたらよいのか？
- 大学レベルの物理と数学の教科書を初めから全部学ばないとならないのか？

そう思うと気が遠くなってしまうことだろう。

でも、あきらめるのはまだ早い。近道があるのだ。今日はそれをお伝えしておこう。

量子コンピュータと量子アルゴリズムを学ぶための前提は「量子力学」と「線形代数」である。理系の大学生にとって、これは当たり前の常識なのだけれど、これらを学んでいない高校生や一般の方の多くがそのことを知らない。理系大学生の常識は世間の常識とは違うことがある。

数式付きで解説されているブルーバックス本を５冊、なるべくわかりやすく、楽しみながら読める本を紹介させていただこう。特に最初の３冊が重要だ。

これらを読み終えれば専門の教科書や以下の関連動画で紹介した専門的な15回の講義が理解できるようになるはずだ。数式を使いながら理解するための最短ルートである。

前提知識がない今のあなたをたとえてみるならば、それは数式をぼんやり見て複数の可能性を同時に考えて混乱している「量子状態」のようなもの。前提知識を得た上で、迷わず焦らず一歩ずつ進める「古典状態」になろう。

以下、紹介する順番にお読みになっていただきたい。

１）量子力学の本

『高校数学でわかるシュレディンガー方程式』（Kindle版）（紹介記事）

大学の物理学科のカリキュラムに沿って順に学ぼうというのならば、力学、電磁気学、解析力学を学んでからやっと量子力学を学び始めることになってしまう。しかし、この本であれば最初の３つを飛ばして量子力学の基礎を学ぶことができるのだ。複素数やオイラーの公式、三角関数や指数関数の微積分など初歩的なことから書かれている。まずこの本で量子の世界のイメージと数式を結び付けよう。量子コンピュータの原理で重要な「ケットベクトル」の意味や計算方法、量子状態の重ね合わせもカバーしている。

第1部シュレディンガー方程式への旅
1 量子力学の誕生
2 波を表す式
3 シュレディンガー方程式
4 波動関数とは

第2部原子の姿
1 波としての電子
2 量子数とはなにか
3 核と核分裂
4 エレクトロニクスと量子力学

第3部シュレディンガー方程式を解く――計算編
1 解析的に解く
2 数値的に解く
3 外からの影響がある場合

『量子もつれとは何か　「不確定性原理」と複数の量子を扱う量子力学』（Kindle版）（紹介記事）

量子コンピュータの計算で重要な量子の絡み合い（エンタングルメント、もつれ）は、この本で詳しく学ぼう。同じ著者の『「シュレーディンガーの猫」のパラドックスが解けた！』（Kindle版）（紹介記事）もお勧めである。猫の生きている状態と死んでいる状態の「重ね合わせ状態」のようなことを光子を使って実現させることができたという話だ。「重ね合わせ」と「絡み合い（もつれ）」の違いはしっかり区別して理解してほしい。

『量子もつれとは何か』の章立て
序章量子力学とは
第1章テクノロジーの進歩と量子化の必要性
第2章振り子の量子化
第3章光の量子化
第4章レーザー光と量子ゆらぎ
第5章量子エンタングルメント
第6章量子光学を用いてEPRペアを生成するための準備
第7章量子光学を用いてEPRペアを生成
第8章量子光学を用いた量子エンタングルメント検証実験
第9章単一光子状態の生成
第10章量子テレポーテーション
第11章多量子間エンタングルメントと量子エラーコレクション実験

２）線形代数の本

『高校数学でわかる線形代数』（Kindle版）

日ごろ数学を敬遠している人でも、上の量子力学の２冊を読み終える頃には線形代数を学ぶ必要性を感じ、モチベーションが高まっているはずだ。この本では固有値と固有ベクトルをはじめ線形代数の基礎的なことがらを学べる。量子コンピュータでは特に複素数の要素をもつ行列、エルミート行列、ユニタリー行列とそれらの計算手順が重要だ。これらをカバーしているのがこの本。読み終えるころには記事トップに掲載した画像の数式が理解できるはずだ。

第1章行列は方程式を解くためのツール
第2章単位行列と逆行列
第3章行列式の登場
第4章行列の数値計算
第5章空間とベクトルの不思議な関係
第6章固有値問題ってなに?
第7章複素数を含む行列
第8章量子力学との関わり

３）量子コンピュータの本

『量子コンピュータ―超並列計算のからくり』（Kindle版）

本格的な専門書に取りかかる前に量子コンピュータ、量子アルゴリズムの全体像をおさえておくと、複雑な「計算の森」で迷子になることが防げる。手っ取り早く知りたいという方にお勧めな本。

第1章量子計算でできること
第2章「量子」とはなにか
第3章量子の不思議
第4章「量子」を使った計算機
第5章量子アルゴリズム
第6章実現にむけた挑戦
第7章量子コンピュータの周辺に広がる世界と量子暗号

４）フーリエ変換の本

『高校数学でわかるフーリエ変換』（Kindle版）（紹介記事）

量子アルゴリズムのひとつに「量子フーリエ変換」がある。だから「フーリエ変換」自体を知らなければ理解できるはずがない。それを学ぶための本だ。量子アルゴリズムの代表格の「ショアの素因数分解アルゴリズム」には量子フーリエ変換アルゴリズム（厳密にいえば逆量子フーリエ変換アルゴリズム）が利用されているので、フーリエ変換は必須項目だ。

第1章フーリエ級数
第2章複素形式への拡張
第3章フーリエ変換への拡張
第4章代表的な関数のフーリエ変換
第5章フーリエ変換の性質
第6章ラプラス変換
第7章ラプラス変換を用いた演算子法

以上、５冊紹介させていただいた。焦らず、じっくり取り組んでほしい。

関連動画：

量子論、量子テレポーテーション、量子コンピュータ

量子の制御とコンピュータ（量子コンピュータの原理の概要説明）

量子コンピュータ授業 #1（15回の講義。本書で解説される量子ゲート、量子アルゴリズムのほとんどを学ぶことができる。）

15回の講義内容

ブログ執筆のはげみになりますので、１つずつ応援クリックをお願いします。

とね日記は長年放置されている科学ブログランキングの不正クリックに対し、次のランキングサイトには適切な運営を期待します。
「FC2自然科学ブログランキング」：不正の例１例２（クリックしてからTwitterアプリで開くと画像は鮮明に見れます。） New-不正の例３
（不正クリックブログの見分け方）

↧

Square root 54,756 using abacus (Double-root method 5)

March 31, 2017, 3:38 am

≫ Next: 開平と開立（第11回）：54,756の算盤による開平（倍根法５）

≪ Previous: 量子コンピュータ、量子アルゴリズムを学びたい高校生のために

[Set 54,756 on Mr. Square root]Zoom

[Japanese]

We will continue from where we ended in the last article, the article shows actual solutions to calculate Square root using abacus. Today's example is simple - basic Double-root method, root is 3-digits case. Please check the Theory page for your reference.

Square root methods: Double-root method, Double-root alternative method, half-multiplication table method, half-multiplication table alternative method, multiplication-subtraction method, constant number method, etc.

Abacus steps to solve Square root of 54,756 (Answer is 234)

"1st group number" is the left most numbers in the 2-digits groups of the given number for square root calculation. Number of groups is the number of digits of the Square root.

54,756 -> (05|47|56) : 5 is the 1st group number. The root digits is 3.

Step 1: Set 54756. 1st group is 5.

Step 2: Square number equal to or smaller than 5 is 4=2^2. 2 is the 1st root. Place 4 which is 2x of 1st root 2. This 4 is double root.

Step 3: Subtract 2^2 from the 1st group 5. 5-4=1 : -a^2

Step 4: Focus on 14 and divide it by double root 4.

Step 5: Answer=3 and this is 2nd root. Set second root 3 on E.

Step 6: Subtract double root 4 x 2nd root 3 from 14. 14-4x3=02.

Step 7: Focus on 27.

Step 8: Subtract (2nd root 3)^2 from 2nd group 27. 27-3^2=18

Step 9: Add 2x2nd root 3 to double root. Set 2x3=6 on B.

Step 10: Focus on double root 46 and 185.

Step 11: Divide 185 by double root 46. Answer=4 reminder 1. Set them on F and I.

Step 12: Subtract (3rd root 4)^2 from 3rd group 16. 16–4^2 =0: -b^2

Step 13: Square root of 54756 is 234.

Final state: Answer 234

Abacus state transition. (Click to Zoom)

Next article is also about Double-root method.

Related articles:

How to solve Cube root of 1729.03 using abacus? (Feynman v.s. Abacus man)
http://blog.goo.ne.jp/ktonegaw/e/cff5d6e7ecaa07230b9cc7af10b23aed

Please place your mouse on the buttons and click one by one. These are blog ranking sites.

↧

開平と開立（第11回）：54,756の算盤による開平（倍根法５）

March 31, 2017, 3:40 am

≫ Next: 発売情報：一般相対性理論を一歩一歩数式で理解する：石井俊全

≪ Previous: Square root 54,756 using abacus (Double-root method 5)

「開平はん」に4,761を置いたところ拡大

[English]

前回に続き、算盤での開平の手順を解説する。今回も倍根法で、根が３桁の場合だ。理論編も参考にしていただきたい。

開平（平方根）：倍根法(2商法)、倍根法別法、半九九法、半九九法別法、乗減法、定数法(折衷法) 、過大数開平、省略開平など

算盤による54,756の2乗根の解法（答は234）

第１群の数とは平方根を求める数を２桁ずつ区切り、いちばん大きい（いちばん左）の２桁のことである。群の数が根の桁数となる。

54756 -> (05|47|56) : 5が第１群の数、根の桁数は3

手順１：54756を置く。第1群は5。

手順２：5以下の平方数は4=2x2。2を初根としてDに立てる。初根2の2倍の4をAに置き、倍根とする。

手順３：2の平方を第1群の5から引く。5-4=1となる。： -a^2

手順４：14に注目し、倍根4で割る。

手順５：商3を得て、割止め、この商を次根とする。次根3をEに置く。： ÷2a

手順６：倍根4と商3の積を14から引く。14-4x3=02。

手順７：27に注目する。

手順８：次根3の平方=9を第2群の27から引く。

手順９：次根3の2倍=6を倍根に加える。つまり2x3=6をBに置く。

手順１０：倍根46と185に注目する。

手順１１：185を倍根46で割り、商4と余り1を得る。第3根の4と余り1をＦ，Ｉに置く。

手順１２：第3根4の平方=16を第3群の16から引く。16-16=00をIJに置く。： -b^2

手順１３：根は234と求まる。

最終状態：答 234

珠の状態推移を表にすると次のようになる。（クリックで拡大）

第１２回も引き続き倍根法による開平を行う。

関連記事：

ファインマン v.s. 算盤の達人：ファインマン先生に立方根計算の雪辱を果たそう
http://blog.goo.ne.jp/ktonegaw/e/89a0b907577f03ef6132cf9664bdcddb

ブログ執筆のはげみになりますので、１つずつ応援クリックをお願いします。

とね日記は長年放置されている科学ブログランキングの不正クリックに対し、次のランキングサイトには適切な運営を期待します。
「FC2自然科学ブログランキング」：不正の例１例２
「にほんブログ村、科学ブログランキング」：New-不正の例１
（不正クリックブログの見分け方）

↧

発売情報：一般相対性理論を一歩一歩数式で理解する：石井俊全

April 1, 2017, 1:18 am

≫ Next: 発売情報：量子プログラミングの基礎：イン・ミンシェン

≪ Previous: 開平と開立（第11回）：54,756の算盤による開平（倍根法５）

「一般相対性理論を一歩一歩数式で理解する：石井俊全」 - 出版社のページ

内容紹介：
いわゆる相対性理論にはアタマに「特殊」と「一般」とつくものがあります。「一般」というのは簡単に言うと、どのような条件でも成り立つ理論という意味であり、「特殊」な状況を切り取った理論より、はるかに複雑で難解なものになります。いまからおよそ100年前、アインシュタインはこの「一般相対性理論」を導きました。これは表面的な概念だけで語れるようなものではありません。それを表現する言語は「数式」以外にないのです。本書は、相対性理論を理解するのに必要な知識を獲得するところから始まり、はじめから一歩一歩着実に、「一般相対性理論」を数式で理解できるよう、徹底的に詳しく解説していきます。
この本は、高校の数学・物理を履修した人向けに書かれています。まず、専門の内容に入る前に、数学、物理の準備をしましょう。次に、相対論を読むときの第一関門となる「テンソル」を具体的な計算をしながら説明します。直線のテンソルを分かったところで、いったん特殊相対性理論に進みます。次に直線のテンソルの話を曲線・曲面のテンソルに拡張し、その中で第二関門である「共変微分」をじっくりと説明します。最後に一般相対論のキーコンセプトとなる曲率の概念を手に入れれば、あとは一気に一般相対性理論を理解することができます。重力場の方程式の一番単純な解から、重力波の方程式までを解説します。
2017年3月27日刊行、672ページ。

著者について：
石井俊全（いしい　としあき）
1965年、東京生まれ。
東京大学建築学科卒、東京工業大学数学科修士課程卒。
大人のための数学教室「和」講師。確率・統計、線形代数から、金融工学、動学マクロ経済に至るまでの幅広い分野で、難しいことを分かりやすく講義している。
石井先生の著書： Amazonで検索

本書のカバーの「そで」には次のように書かれている。

一般相対性理論の発表から100年が経過しました。もうそろそろ、一般相対性理論を数式レベルで理解する人たちが爆発的に増えてもいい頃ではないでしょうか。

爆発的増加は無理としても小規模爆発くらいはしてほしいと僕も思うわけで、著者の石井先生と同じ気持ちから8年前に「一般相対性理論に挑戦しよう！」という記事を書いたことがある。この記事の中核になるのが広江克彦さんがお書きになった「趣味で相対論」という本だ。数式を使わない科学教養書と数式だらけの専門書の中間的位置づけの「副読本」、「準教科書」のような切り口で、2008年の発売以来多くの物理ファンの心をつかんできた。

今日紹介する「一般相対性理論を一歩一歩数式で理解する：石井俊全」も教養書と専門書の間をつなぐ位置付けにある本で先月末に発売されたばかりだ。これまで刊行された石井先生の著書が素晴らしかっただけに、期待できる本なのだろう。さっそく中身を調べてみた。

相対性理論の教科書、副読本（準専門書）の種類

相対性理論を解説した教科書、副読本は、いくつかのタイプに分類できる。

１）物理学的視点から書かれた本、数学的視点から書かれた本

著者の石井先生は数学がご専門なので本書は数学的視点から解説した本である。同様に数学的視点から書かれた本では「時空の幾何学：特殊および一般相対論の数学的基礎」が知られている。

その他の教科書のほとんどは物理学的視点から書かれた本だ。

２）アインシュタインの重力場の方程式の扱い方の違い

一般相対性理論の根幹はアインシュタインの重力場の方程式だ。その導出にはリーマン幾何学の複雑なテンソル計算が必要である。この部分を詳しく解説するか、しないかで本の特色の違いがでてくる。

本書はこの方程式の導出を省略することなく解説している。「時空の幾何学：特殊および一般相対論の数学的基礎」と「趣味で相対論」もこの点については同様だ。

物理現象、応用に焦点、数値相対論に重点を置いた本ではこの方程式の導出は大まかにしか行われない。ハートルの「重力（上）（下）」、柴田先生の「一般相対論の世界を探る―重力波と数値相対論」などがこれに該当する。

方程式の導出を読者の演習として学ばせる本もある。中級レベルの教科書として知られている須藤先生の「一般相対論入門：須藤靖」、「もうひとつの一般相対論入門：須藤靖」がこれに該当する。

上級者向けに、より発展的な内容に重点を置いた本がある。内山先生の「一般相対性理論」、「一般ゲージ場論序説」がこれに該当し、Reissner-Weyl解（荷電粒子のまわりの静的・球対称な時空）や、Kerr解などの導出、重力のゲージ場理論までを解説している。

百科事典的な本もある。「重力理論 Gravitation-古典力学から相対性理論まで、時空の幾何学から宇宙の構造へ」はほぼすべての項目を含み、「黒い電話帳」として学生、専門家の間で重宝されている。ただし日本語版は翻訳の質がよくないので、英語版をお勧めしたい。

相対性理論の本は、この他ここに紹介できないほどたくさんあるのは言うまでもない。

本書の構成、特色

- 構成、数学と物理の割合

670ページの分厚い本になったのは相対性理論を解説するために必要な数学の解説をすべて含めたためだ。これ１冊で完結しているコンプリートな本である。ページ占有率は数学６、物理学４という割合。章立ては次のとおりだ。

第1章数学の準備
第2章物理の準備
第3章テンソルと直線座標のテンソル場
第4章特殊相対性理論
第5章曲線座標のテンソル場
第6章曲率
第7章一般相対性理論

- 安い

ページ数がこれだけあり、相対性理論を理解するためのすべてが詰まっているのに定価は3500円（＋消費税）。居酒屋、焼き肉屋１回分のお金で相対性理論を自分のものにできるのだから激安である。

- テンソルの解説を前倒しにしていること

ベクトル解析、テンソル解析を前倒しに解説しているのが他の本に見られない特色だ。数学と物理の記述は章ごとに交互になるよう置かれているが、ベクトル場、テンソル場、リーマン幾何学など、それぞれなるべく早い時点で説明してから、それらを使う物理の解説を展開している。

テンソル場はまず直線のテンソル場を解説し、次に曲面のテンソル場への一般化、そして第二関門である「共変微分」、最終関門である「曲率の概念」へと進んでいく。

- 特殊相対性理論と一般相対性理論

本書がユニークなのは特殊相対性理論と一般相対性理論の連続的なつながりが理解できるところにある。特殊相対性理論で使われる数式は中学、高校レベルの易しいものであるのに対し、一般相対性理論ではテンソル解析、多次元微分幾何学という難易度が全く違う数学が使われる。したがって本書以外の本ではこの２つの理論が分断されている別々の理論のように思えてしまう。

けれども本書ではテンソルの説明を前倒しにすることで、特殊相対性理論と一般相対性理論の連続的なつながりが明らかになり、文字通り特殊相対性理論が一般相対性理論の特殊な場合であることが理解できるのだ。

- 電磁気学も解説、マックスウェル方程式の４元化

古典電磁気学、マックスウェル方程式を詳しく解説している。特殊相対性理論には欠かせない電磁気学を省略していないことはページ数が増えた理由のひとつだ。古典電磁気学は広江さんの著書では「趣味で物理学」に含まれている。そして「マックスウェル方程式を１本にまとめたのは誰？」という記事で紹介したような特殊相対性理論による電磁気学の４次元化、ローレンツ変換の解説へとつないでいる。

- 驚異の定理への言及

リーマン幾何学では「曲率の概念」は特に重要だ。数学がご専門だけにガウスの功績、「驚異の定理」への言及もされている。この定理については「宇宙の形、ガウスの曲面論と内在幾何」という連載記事をお読みいただきたい。

- 双子のパラドックス、重力波

科学教養書ではなかなか納得できない「双子のパラドックス」を数式でていねいに説明している。ページ数の都合でとかく省略されてしまいがちなこの現象が解説されているのはうれしい。

また、重力波の方程式が導出されているのも本書の長所だ。「重力波の直接観測に成功！」というニュースは昨年話題になったばかり。新しい本の強みだといえよう。

- ニュートンの場の理論

これもページ数の都合で割愛されてしまいがちな内容だ。ベクトル解析を解説した後、高校で習うニュートンの運動方程式を復習し、さらに高校では習わない場の方程式として紹介する。アインシュタインの場の方程式に対応するものがニュートン力学の段階ですでにあることをこの本を読む初学者は学ぶことができる。

- 数学といっても定理の証明をしているわけではない

数学としての解説が多いといっても、本書は高校３年レベルの数学と物理学を学んだ人を対象にしているわけだから、同じ著者の「ガロア理論の頂を踏む」のように定理、証明を厳密な形で積み重ねていくような専門書ではない。全体的に数式で埋め尽くされているページが多いが、それは詳しく手順を追って式変形を紹介しているからだ。本のタイトルにあるとおり「一歩一歩」進めば初学者でもついていける本だ。

「趣味で相対論」との比較

- ページ数の違いについて

アインシュタインの重力場の方程式の導出を「ごまかしなく解説する」という意味では「趣味で相対論」は本書と同じである。しかしこちらは273ページしかない。どういうことだろうか？

それは本書で解説されているニュートン力学と古典電磁気学を広江さんは「趣味で物理学」のほうにお書きになっているからだ。またベクトル解析は書籍化されていない「EMANの物理数学」の一部としてお書きになっている。

すべてを書籍化して１冊にまとめれば、広江さんの本のほうも本書と同じようなページ数になるのではないかと僕は思っている。

広江さんは大学で物理学を専攻されていたので、物理的な視点、発想で相対性理論を解説されている。ここは本書と大きく違うところだ。

また広江さんの本は本書と比べて文章が多い。ご自身への問いかけ、感動をそのままお書きになっているから読み物としての面白味や味わいがある。それに対し本書は「感情の露出」が控えめである。地道に一歩ずつ階段を上るようなイメージで読み進めることになる。

数式で学ぶ相対性理論の入門書としてどちらがよいのかは決められない。読者の好みや忍耐力に左右されるのだと思う。

「時空の幾何学：特殊および一般相対論の数学的基礎」との比較

数学からの視点から書かれたという意味で「時空の幾何学：特殊および一般相対論の数学的基礎」は本書と同じ側面をもっている。

けれども「時空の幾何学」は大学で数学を専攻している学生向けであり、本書のような高校卒業レベルの人を対象にしているわけではない。

特に「時空の幾何学」は相対性理論の幾何学的イメージを強調していて、特殊相対性理論では三角関数や双曲三角関数が多用されている。またリーマン幾何学に入る直前の章ではガウスの内在幾何の解説に多くのページを割いている。いかにも数学科の学生が好みそうな様相に仕上がっているのだ。ビジュアルで美しい図版が多いのも「時空の幾何学」の特色だ。

また「時空の幾何学」には電磁気学についての記述はマックスウェルの方程式とローレンツ変換について５ページの解説があるだけである。

著者からのメッセージ

本書のカバーの「そで」には著者からのメッセージが書かれている。この中で石井先生は「私は数学・物理学を専門にしている研究者ではない」と、しきりに「素人ぶり」を強調されている。「まえがき」には「大学受験の物理の問題を解ける自信もない」ともお書きになっている。

謙遜しすぎだと思ったが、たとえそれが本当だとしても石井先生は多くの人がもっている「一般相対性理論を理解したい」という夢をかなえたおひとりだということ、その感動を多くの人に感じてもらいたいという思いが込められている。カバーの「そで」に書かれているメッセージは本のページには含まれていないので、カバーはなくさずに持っておきたい。

僕の感触、感想

広江さんの「趣味で相対論」を読んだとき、こんなにわかりやすいの？と衝撃を受けたのだが、本書が登場したことで、もうひとつ選択肢が増えたことになる。

今の学生は幸せだなとつくづく思うのだ。どちらを先に読むかはあなた自身で決めていただきたい。どちらにも一長一短があるという言い方はあてはまらない。どちらの本を選ぶかは、相対性理論が到達した山頂を目指して数学の風景を見ながら登るか、物理学の風景を見ながら登るかの違いなのだ。

今回は大ざっぱにページをめくったうえでの紹介記事である。実際に読むとまた新しい発見や気づきがあることだろう。本書を通読してから正式な紹介記事を書くつもりだ。

関連記事：

一般相対性理論に挑戦しよう！
http://blog.goo.ne.jp/ktonegaw/e/ea7ad9292ce01ad4abbbc8c98f3303d0

趣味で物理学：広江克彦
http://blog.goo.ne.jp/ktonegaw/e/90aa60383b600ff4e4fd7bea6589deaa

趣味で相対論：広江克彦
http://blog.goo.ne.jp/ktonegaw/e/90aa60383b600ff4e4fd7bea6589deaa

時空の幾何学：特殊および一般相対論の数学的基礎
http://blog.goo.ne.jp/ktonegaw/e/ffc643a688ce45dec7460d107fe1392e

重力(上) アインシュタインの一般相対性理論入門：ジェームズ・B・ハートル
http://blog.goo.ne.jp/ktonegaw/e/d45a93d43478a133c6a514c980572632

重力(下) アインシュタインの一般相対性理論入門：ジェームズ・B・ハートル
http://blog.goo.ne.jp/ktonegaw/e/ae6e91eec0ecb404b3b77d46ca04b49b

重力理論 Gravitation-古典力学から相対性理論まで、時空の幾何学から宇宙の構造へ
http://blog.goo.ne.jp/ktonegaw/e/f838b8f6c2554000933187df89e08013

日本物理学会2016年度公開講座「一般相対性理論と宇宙－重力波研究の最前線－」
http://blog.goo.ne.jp/ktonegaw/e/d39ec747fb47e0c8418e7e167e2f60c4

マックスウェル方程式を１本にまとめたのは誰？
http://blog.goo.ne.jp/ktonegaw/e/226568b2c27822fb9fdfdb088e7018d3

マーミン相対論―新しい発想で学ぶ：デヴィッドマーミン
http://blog.goo.ne.jp/ktonegaw/e/6e47253b0622e867f57fb15b88d18149

ブログ執筆のはげみになりますので、１つずつ応援クリックをお願いします。

「一般相対性理論を一歩一歩数式で理解する：石井俊全」 - 出版社のページ

↧

発売情報：量子プログラミングの基礎：イン・ミンシェン

April 2, 2017, 2:42 am

≫ Next: 裳華房の基礎数学選書がKindle化され始めた件

≪ Previous: 発売情報：一般相対性理論を一歩一歩数式で理解する：石井俊全

「量子プログラミングの基礎：イン・ミンシェン」 - 出版社のページ

内容紹介：
本書は量子プログラミング分野について詳細かつ体系的な解説を与えることを意図している。特定の言語や技術に焦点を当てるよりも，基本的な概念，手法，数学的ツールに重点を置く。量子力学と量子計算の基本的知識から始めて，さまざまな量子プログラムの構成要素や一連の量子プログラミングモデルを詳しく紹介し，さらに量子プログラムの意味論や論理，検証解析技術を体系的に論じる。プログラミング言語に通じた人が理解しやすいよう，詳細を具体的に提示して可能な限り自己完結するように努めた。
2017年4月7日刊行、456ページ。

著者について：
イン・ミンシェン（Mingsheng Ying）HP: http://quantum-lab.org/mingsheng/
Mingsheng Ying (h-index: 34) is currently a Distinguished Professor at the University of Technology Sydney (UTS) and Research Director of the Center for Quantum Computation and Intelligent Systems, at UTS. He was the Cheung Kong Chair Professor, in the Department of Computer Science and the Scientific Director of the National Key Laboratory of Intelligent Technology and Systems at Tsinghua University. His research interests are quantum computation and quantum information, programming language theory and artificial intelligence. In 2008 he received The National Science and Technology Award for contributions in computer science from China.

He is an Associate Editor of Artificial Intelligence (Elsevier) and he has published more than 100 papers in top international journals and conferences such as ACM Transactions on Programming Languages and Systems, Artificial Intelligence, IEEE Transactions on Information Theory, IEEE Transactions on Software Engineering, Information and Computation, Journal of Computer and System Sciences, Physical Review Letters, POPL, CONCUR, IJCAI. He is also the author of the book Topology in Process Calculus - Approximate Correctness and Infinite Evolution of Concurrent Programs (Springer 2001).

「クラウド量子計算入門：中山茂」で量子アルゴリズムを学んでいるところなのだが、気になる本が発売されるそうなので発売情報としてお知らせすることにした。

プログラミング言語の設計や開発をするための本は、易しいものから専門家向けのものまでいくつも出版されているが、それらはすべて現在のコンピュータ用のものだ。でも本書は違う。なんと量子コンピュータ用のプログラミング言語の設計方法やプログラミングを解説した本である。本の紹介ツイートを見たとき「ええっ！何それ？？」と目を疑った。ツイートはてっきりエイプリルフールのネタかと。。。

早すぎる。だって今はやっと量子論理ゲートを組み合わせてひとつずつアルゴリズムを組み立てている段階でしょ？それを現在のコンピュータにたとえるならば学研の「電子ブロックFX-SYSTEM FX-マイコンR-165」や「４ビットマイコン GMC-4」の段階にもなっていないわけだから。これらのマイコンは16進数の機械語でプログラミングしてから実行するコンピュータだ。

FX-SYSTEM FX-マイコンR-165と４ビットマイコン GMC-4（クリックで拡大）

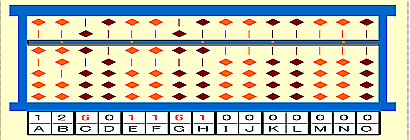
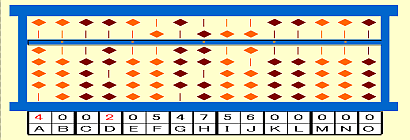
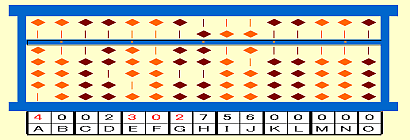
いま学んでいる五線譜のような「IBMの量子コンピュータ」のスコアにドラッグ＆ドロップして並べた量子アルゴリズムを眺めていると、やはりこれは古典的4ビットマイコン以前のやり方だと思った。

僕が量子論理ゲートを配置していく操作は「結線論理（ワイヤードロジック）」あるいは「ランダム論理」と同じようなものだ。なぜなら色のついた四角形であらわされるひとつひとつの量子論理ゲートが古典コンピュータのAND回路、OR回路のような論理ゲートに対応しているわけだから。

ランダム論理というのはICがまだ普及していなかった1960年代、卓上電卓がようやく登場したころに使われていた方法のこと。大多数のメーカーが電卓の回路として採用していたのは「ランダム論理」というもので計算手順をすべてトランジスターやコンデンサ、抵抗やダイオードを使って組み上げたAND、OR、NOT、NORなどの論理ゲートを組み合わせて配線するものだった。電卓は何かキーが押されるたびに内部の状態が推移していくのだが、その状態推移や計算そのものをすべて電子素子の回路として実現していたわけである。電子回路のトポロジーと部品そのものが加減乗除のアルゴリズムを実行していたのだ。そしてアルゴリズムごとに回路も違ってくる。いま学んでいる量子アルゴリズムで章ごとに回路を組みなおしているのと同じことだ。（参考記事：「電卓を作りたいという妄想」）

ほとんどの電卓メーカーがこのランダム論理を採用していたが、なかにはビジコン社のように現在のコンピュータのような「プログラム論理（Program Logic）」を採用した電卓を開発、販売しているメーカーもあった。ビジコン社の電卓はキー操作による状態推移や計算自体をマクロ化したプログラム論理を採用していた。つまりコンピュータ化しやすい設計方針だったのである。この手法が後にCPUやマイコンの誕生をもたらしたのだ。このことは「マイクロコンピュータの誕生―わが青春の4004：嶋正利」という記事で紹介したことがある。

もうひとつ気付いたことがある。「ファインマン計算機科学：ファインマン, A.ヘイ, R.アレン」の第５章の「可逆計算と計算の熱力学」に書かれていることだ。ファインマン先生はコンピュータの消費電力を最小限に抑えるために可逆な論理回路に基づく計算機の必要性を説いている。CPUから発生する熱は電流が流れることによるジュール熱の他、不可逆な計算処理に伴う熱エネルギーなのである。代表的な論理回路であるAND回路やOR回路は次の図に示すとおり２つのAとBという入力について計算を行なって１つの出力Xを得る。

これは情報から熱という形でエネルギーを取り出せることを意味している。

情報をエネルギーに変換することに成功！（2010年11月）
https://www.s.u-tokyo.ac.jp/ja/press/2010/42.html

このことの本質は「あらゆる不可逆な物理現象は熱の発生を伴う。」という「熱力学第２法則」だ。両手をこすったときの摩擦によって熱が出るのもその一例である。

「計算する」という現象も不可逆過程だ。「３＋２＝５」のような２項演算はすべて不可逆計算だということである。つまり３と２という２つの入力に対して５という１つの出力を得るわけだが、出力の５から入力が３と２だということが再現できない。もしかすると入力が４と１の可能性もあるわけだから。計算することで情報が失われているのである。そして失われた情報は熱として放出されるのだ。（人間が暗算で３＋２＝５を計算するときも同様で熱が放出されている。）

しかし、量子コンピュータの回路を見ると各ゲートの入力と出力の数は等しい。量子論理ゲートを五線譜上に配置しているだけだから。つまりこのコンピュータはファインマン科学の本で説明されている意味での「可逆コンピュータ」なのである。

ともあれ現在の量子コンピュータはこのように機械語以前の原始的な段階だということはおわかりだろう。もちろんアルゴリズムごとに量子ゲートを配置するのでは面倒極まりない。一度に実行できる量子ビット数が増え、アルゴリズムが複雑化すればお手上げになるのは目に見えていいる。

だから現在のコンピュータのC言語、Java言語のように人が理解できるプログラミング言語が量子コンピュータにも必要になるわけだ。そしてそのプログラミング言語はどのようなものであるべきなのか。

量子アルゴリズムは古典アルゴリズムと全く違う。量子プログラミング言語も現在のプログラミング言語とはずいぶん違うものになるのだろう。

将来を見据えて量子コンピュータ用のプログラミング言語のもとになる概念や理論、言語設計、プログラミングモデルを解説しているのが本書なのである。2003年に「Structured Quantum Programming」というPDF文書が書かれていたようだが、翻訳のもとになった原書も含めて、この分野の専門書が市販本として刊行されるのは初めてのことだと思う。章立ては以下のとおり。

-------------------------------------
I　量子プログラミングの概要と準備
-------------------------------------
1　はじめに
2　予備知識
--------------------------------------
II　古典的制御をもつ量子プログラム
--------------------------------------
3　量子プログラムの構文と意味論
4　量子プログラムの論理
5　量子プログラムの解析
---------------------------------------
III　量子的制御をもつ量子プログラム
---------------------------------------
6　量子的場合分け文
7　量子的再帰
------------------
IV　今後の展望
------------------
8　今後の展望

記事のいちばん下に載せた詳細目次を見ると「ヒルベルト空間」や「フォック空間」などの数学用語が目に入る。どちらも関数解析という分野の数学的な空間で、それぞれ量子力学、量子場（多粒子系の量子力学）を数学的に定式化するものだ。どちらも数理物理という分野である。なぜフォック空間のようなものが必要になるのかなと思ったが、目次を見ると「量子的再帰プログラム」に使われるようだ。

ヒルベルト空間に関する教科書では次の記事を書いたことがある。

ヒルベルト空間と量子力学：新井朝雄
http://blog.goo.ne.jp/ktonegaw/e/fa4d9da634afbdb8a9dfc1ac162f7afe

発売情報：ヒルベルト空間と量子力学改訂増補版：新井朝雄
http://blog.goo.ne.jp/ktonegaw/e/84313bfed4331fe0c1343a55a531809a

量子力学の数学的構造 I：新井朝雄、江沢洋
http://blog.goo.ne.jp/ktonegaw/e/196b59dc50fca361ba523036e7eeb908

量子力学の数学的構造 II：新井朝雄、江沢洋
http://blog.goo.ne.jp/ktonegaw/e/a4ef01e94a8c0384cec353ebe4d542e4

フォック空間は１粒子ヒルベルト空間のテンソル積の直和で作られるヒルベルト空間として定義されるものだ。まだ読んでいないが、次の本で学ぶことができる。

フォック空間と量子場(上)：新井朝雄
https://www.nippyo.co.jp/shop/book/1356.html
https://www.nippyo.co.jp/shop/book/6224.html

フォック空間と量子場(上)：新井朝雄
https://www.nippyo.co.jp/shop/book/1357.html
https://www.nippyo.co.jp/shop/book/7190.html

このようなわけで、本書を読み解くためには量子コンピュータだけでなく量子力学やそれを定式化するヒルベルト空間、フォック空間などの数学、プログラミング言語設計と開発など多方面の知識が必要だ。なかなか手ごわそうである。

翻訳のもとになった英語版は昨年3月に刊行されたばかり。米国アマゾンで見てもまだ読者レビューが書かれていないどころか、星マークもつけられていない。買うのには少し勇気がいる。

「Foundations of Quantum Programming (2016): Mingsheng Ying」（Kindle版）

このように未来の技術を先取りした本を、いち早く紹介するために日本語版の翻訳をしてくださった川辺治之氏（@p314159265）に感謝したい。ネットで調べるとわかるが、たくさんの本をこれまでに翻訳されている方だ。

川辺治之氏の訳書： Amazonで検索

未来のプログラミングの世界を垣間見たい方は、ぜひお買い求めいただきたい。（レベルが高い本のようだから、書店で立ち読みしてからにしたほうがよいかもしれないが。）

発売前なので、今日の記事の前半は本書の内容の周辺の話になってしまった。本の内容は以下の詳細目次から想像していただきたい。

関連記事：

発売情報：クラウド量子計算入門：中山茂
http://blog.goo.ne.jp/ktonegaw/e/d360b69100fbe723c5b9410dbf3f5f4d

量子コンピュータ、量子アルゴリズムを学びたい高校生のために
http://blog.goo.ne.jp/ktonegaw/e/1b2940b648bda682aa27192eb8261972

ファインマン計算機科学：ファインマン, A.ヘイ, R.アレン
http://blog.goo.ne.jp/ktonegaw/e/4f7f453019fd463ed2bfdeaa7b288d79

マイクロコンピュータの誕生―わが青春の4004：嶋正利
http://blog.goo.ne.jp/ktonegaw/e/fe74cdf21a2be8999cb101cc62018f8b

安田寿明先生の「マイ・コンピュータ」３部作（ブルーバックス）
http://blog.goo.ne.jp/ktonegaw/e/e54e4eb38380ff2ff2f51747ca7b4f75

ブログ執筆のはげみになりますので、１つずつ応援クリックをお願いします。

「量子プログラミングの基礎：イン・ミンシェン」 - 出版社のページ

-------------------------------------
　I　量子プログラミングの概要と準備
-------------------------------------

1　はじめに
　1.1　量子プログラミング研究のおおまかな歴史
　　1.1.1　量子プログラミング言語の設計
　　1.1.2　量子プログラミング言語の意味論
　　1.1.3　量子プログラムの検証と解析
　1.2　量子プログラミングへのアプローチ
　　1.2.1　データの重ね合わせ―古典的制御をもつ量子プログラム
　　1.2.2　プログラムの重ね合わせ―量子的制御をもつ量子プログラム
　1.3　本書の構成

2　予備知識
　2.1　量子力学
　　2.1.1　ヒルベルト空間
　　2.1.2　線形作用素
　　2.1.3　ユニタリ変換
　　2.1.4　量子測定
　　2.1.5　ヒルベルト空間のテンソル積
　　2.1.6　密度作用素
　　2.1.7　量子操作
　2.2　量子回路
　　2.2.1　基本的定義
　　2.2.2　1量子ビットゲート
　　2.2.3　制御ゲート
　　2.2.4　量子マルチプレクサ
　　2.2.5　量子ゲートの万能性
　　2.2.6　回路中での測定
　2.3　量子アルゴリズム
　　2.3.1　量子並行性と量子干渉
　　2.3.2　ドイチュ-ジョザのアルゴリズム
　　2.3.3　グローバーの探索アルゴリズム
　　2.3.4　量子ウォーク
　　2.3.5　量子ウォーク探索アルゴリズム
　　2.3.6　量子フーリエ変換
　　2.3.7　位相推定
　2.4　文献等についての補足

--------------------------------------
　II　古典的制御をもつ量子プログラム
--------------------------------------

3　量子プログラムの構文と意味論
　3.1　構文
　3.2　操作的意味
　3.3　表示的意味
　　3.3.1　意味関数の基本性質
　　3.3.2　量子プログラムの意味領域
　　3.3.3　ループの意味関数
　　3.3.4　量子変数の変更とアクセス
　　3.3.5　停止確率と発散確率
　　3.3.6　量子操作としての意味関数
　3.4　量子プログラミングにおける古典的再帰
　　3.4.1　構文
　　3.4.2　操作的意味
　　3.4.3　表示的意味
　　3.4.4　不動点による特徴づけ
　3.5　例を用いた説明：グローバーの量子探索
　3.6　補題の証明
　3.7　文献等についての補足

4　量子プログラムの論理
　4.1　量子述語
　　4.1.1　量子最弱事前条件
　4.2　量子プログラムのフロイド-ホーア論理
　　4.2.1　正当性論理式
　　4.2.2　量子プログラムの最弱事前条件
　　4.2.3　部分正当性の証明系
　　4.2.4　全正当性の証明系
　　4.2.5　例による説明：グローバーのアルゴリズムの正当性
　4.3　量子的最弱事前条件の可換性
　4.4　文献等についての補足

5　量子プログラムの解析
　5.1　量子的whileループの停止性の解析
　　5.1.1　ユニタリ変換を本体とする量子的whileループ
　　5.1.2　一般の量子的whileループ
　　5.1.3　平均実行時間の計算例
　5.2　量子グラフ理論
　　5.2.1　基本的定義
　　5.2.2　底強連結成分
　　5.2.3　状態ヒルベルト空間の分解
　5.3　量子マルコフ連鎖の到達可能性解析
　　5.3.1　到達可能性確率
　　5.3.2　反復到達可能性確率
　　5.3.3　永続性確率
　5.4　補題の証明
　5.5　文献等についての補足

---------------------------------------
　III　量子的制御をもつ量子プログラム
---------------------------------------

6　量子的場合分け文
　6.1　古典的場合分け文から量子的場合分け文へ
　6.2　量子的場合分け文をもつ言語QuGCL
　6.3　量子操作のガード付き合成
　　6.3.1　ユニタリ作用素のガード付き合成
　　6.3.2　作用素値関数
　　6.3.3　作用素値関数のガード付き合成
　　6.3.4　量子操作のガード付き合成
　6.4　QuGCLプログラムの意味論
　　6.4.1　古典的状態
　　6.4.2　QuGCLの準古典的意味論
　　6.4.3　純粋量子的意味論
　　6.4.4　最弱事前条件の意味論
　　6.4.5　例
　6.5　量子選択
　　6.5.1　古典的選択から確率的選択を経て量子選択へ
　　6.5.2　確率的選択の量子的実装
　6.6　代数的規則
　6.7　例による説明
　　6.7.1　量子ウォーク
　　6.7.2　量子位相推定
　6.8　考察
　　6.8.1　量子操作のガード付き合成の係数
　　6.8.2　部分空間をガードとする量子的場合分け文
　6.9　補題，命題，定理の証明
　6.10　文献等についての補足

7　量子的再帰
　7.1　量子的再帰プログラムの構文
　7.2　再帰的量子ウォーク
　　7.2.1　再帰的量子ウォークの仕様
　　7.2.2　いかにして量子的再帰式を解くか
　7.3　第二量化子
　　7.3.1　多粒子状態
　　7.3.2　フォック空間
　　7.3.3　フォック空間の観測量
　　7.3.4　フォック空間の時間発展
　　7.3.5　粒子の生成と消滅
　7.4　自由フォック空間における再帰式の解
　　7.4.1　自由フォック空間の作用素の意味領域
　　7.4.2　プログラム図式の意味汎関数
　　7.4.3　不動点を用いた意味論
　　7.4.4　構文的近似
　7.5　対称性および反対称性の回復
　　7.5.1　対称化汎関数
　　7.5.2　量子的再帰プログラムの意味関数の対称化
　7.6　量子的再帰の主量子系の意味論
　7.7　例による説明：再帰的量子ウォーク
　7.8　（量子的制御をもつ）量子的whileループ
　7.9　文献等についての補足

------------------
　IV　今後の展望
------------------

8　今後の展望
　8.1　量子プログラムと量子機械
　8.2　量子プログラミング言語の実装
　8.3　関数型量子プログラミング
　8.4　量子プログラムの圏論的意味論
　8.5　並列量子プログラムから量子的並列性へ
　8.6　量子プログラミングにおける量子もつれ
　8.7　量子系のモデル検査
　8.8　物理学への量子プログラミングの適用

参考文献

索引

↧

裳華房の基礎数学選書がKindle化され始めた件

April 5, 2017, 9:03 am

≫ Next: Square root 237,169 using abacus (Double-root method 6)

≪ Previous: 発売情報：量子プログラミングの基礎：イン・ミンシェン

Kindle化された裳華房の基礎数学選書

先日「裳華房の基礎数学選書がKindle化されている！」とツイートしたところ思わぬ反響があった。ついに専門書、大学の教科書レベルの本も電子書籍化が始まったのかと期待させてくれるからかもしれない。他社について、状況はどうなのだろうか？

工学系、化学系の本にくらべて物理学系、数学系の専門書の電子書籍化は遅れているようである。

「出版社名＋物理」、「出版社名＋数学」という検索キーで理数系書籍を多く刊行している出版社別に調べてみた。今のところ裳華房以外は期待外れだったが、これから力を入れ始める出版社がでてくるかもしれないので、ときどきこの記事を開いて検索してみるとよいだろう。

すでにKindle化されている物理、数学書については「電子書籍（Kindle）で読める日本語の理数系書籍の検索ページ」から検索していただきたい。

なお、Kindle本のキーワード検索結果ではマッチするすべての本が表示されないようだ。あくまでKindle本がでているかどうかの目安としてお考えいいただきたい。ご自身で検索ワードをいろいろ変えて検索しなおしてみることをおすすめする。

Kindle化されている本が見つかった出版社

裳華房：：物理　化学　量子化学　数学

いくつもの物理学、数学のシリーズが思い浮かぶ。順に電子書籍化してほしい。

講談社：物理　数学

電子書籍化がいちばん進んでいる。ブルーバックスだけでなく専門書、教科書レベルの本も電子書籍化が始まったようだ。

筑摩書房：（ちくま学芸文庫）

ちくま学芸文庫の電子書籍化が始まったのが特にうれしい。

技術評論社：物理　数学

専門書、教科書レベルの本のKindle化はまだのようだが、準教科書レベルの良書が多い。

秀和システム：物理　数学

準教科書レベルの物理学書が中心。Kindle化が少しずつ始まっている。

ベレ出版：物理　数学

準教科書レベルの数学書でKindle化が始まったようだ。特に石井俊全先生の本をKindle化してほしいところ。

岩波書店：物理　数学

非常に多くの物理学、数学書のシリーズをもっている出版社。数学からKindle化が始まったようだ。新書や文庫だけでなく専門書の電子書籍化に期待したい。

日本評論社：物理　数学

準教科書レベルの数学書Kindle版が１冊見つかっただけ。

共立出版：物理　数学

非常に多くの物理学、数学の専門書があるのに、Kindle化されているのは「マンガでわかる統計学」のような本だけ。

みすず書房：物理　数学

理数系だけでなく人文・社会系も含めて素晴らしい本が多い出版社。いまのところ数学(?)の教養書が１冊Kindle版で見つかっただけなので、ぜひ電子書籍化を進めてほしい。

Kindle化されている本が見つからなかった出版社

以下も物理学徒、数学徒ならば必ず知っている出版社。それぞれ専門書のシリーズ名がいくつか思い浮かぶことだろう。裳華房に続き、ぜひ電子書籍化に力を入れてほしい。

朝倉書店：物理　数学

吉岡書店：物理　数学

東京図書：物理　数学

東京大学出版会：物理　数学

森北出版：物理　数学

培風館：物理　数学

丸善出版：物理　数学

関連記事：

電子書籍（Kindle）で読める日本語の理数系書籍の検索ページ
http://blog.goo.ne.jp/ktonegaw/e/347122df8d808286fd47e6fe9788de2d

ブログ執筆のはげみになりますので、１つずつ応援クリックをお願いします。

↧

Square root 237,169 using abacus (Double-root method 6)

April 8, 2017, 2:10 am

≫ Next: 開平と開立（第12回）：237,169の算盤による開平（倍根法６）

≪ Previous: 裳華房の基礎数学選書がKindle化され始めた件

[Set 237,169 on Mr. Square root]Zoom

[Japanese]

We will continue from where we ended in the last article, the article shows actual solutions to calculate Square root using abacus. Today's example is simple - basic Double-root method, root is 3-digits case. We require root reduction in the steps. Please check the Theory page for your reference.

Square root methods: Double-root method, Double-root alternative method, half-multiplication table method, half-multiplication table alternative method, multiplication-subtraction method, constant number method, etc.

Abacus steps to solve Square root of 237,169 (Answer is 487)

"1st group number" is the left most numbers in the 2-digits groups of the given number for square root calculation. Number of groups is the number of digits of the Square root.

237169 -> (23|71|69) : 23 is the 1st group number. The root digits is 3.

Step 1: Set 237169. 1st group is 23.

Step 2: Square number smaller than or equal to 23 is 16=4^2. 4 is the 1st root.

Step 3: Subtract 4^2 from the 1st group 23. 23-16=07

Step 4: Place 8 which is 2x of 1st root 4. This 8 is double root. Focus on 77.

Step 5: Divide 77 by 8. Answer=9 and this is 2nd root.

Step 6: Subtract 8x9=72 from 77. Place 05 on FG.

Step 7: You cannot subtract 9^2 (=81) from the 51 on GH, so the 2nd root 9 is over-root. Subtract 1 from 2nd root 9 then replace the 2nd root as 8, give back the double-root 8. Place 05+08=13 on FG.

Step 8: Focus on 2nd root 8 and 131 on FGH.

Step 9: Subtract 8^2 from 131 (FGH) and set the answer 067 to FGH.

Step 10: Focus on double-root 80 and 2nd root 8.

Step 11: Add 2 x 2nd root 8 (=16) to double-root 80. Place 2x8+80=96 on AB.

Step 12: Divide 676 on GHI by double-root 96.

Step 13: Answer=7 and this is 3rd root. Place 3rd root 7 on F. Place remainder 676-96x7=004 on GHI.

Step 14: Focus on 3rd root 7 and 3rd group 49 on IJ.

Step 15: Subtract 7^2 from 3rd group 49. Place 49-49=00 on IJ.

Step 16: Square root of 237169 is 487.

Final state: Answer 487

Abacus state transition. (Click to Zoom)

↧

開平と開立（第12回）：237,169の算盤による開平（倍根法６）

April 8, 2017, 2:13 am

≫ Next: クラウド量子計算入門：中山茂：(3) 前回の記事の訂正

≪ Previous: Square root 237,169 using abacus (Double-root method 6)

「開平はん」に237,169を置いたところ拡大

[English]

前回に続き、算盤での開平の手順を解説する。今回も倍根法で、根が３桁、過大根が生じ途中で根を還元する必要がでてくる。理論編も参考にしていただきたい。

開平（平方根）：倍根法(2商法)、倍根法別法、半九九法、半九九法別法、乗減法、定数法(折衷法) 、過大数開平、省略開平など

算盤による237,169の2乗根の解法（答は487）

第１群の数とは平方根を求める数を２桁ずつ区切り、いちばん大きい（いちばん左）の２桁のことである。群の数が根の桁数となる。

237169 -> (23|71|69) : 23が第１群の数、根の桁数は3

手順１：237169を置く。第1群は23。

手順２：23以下の平方数は16=4x4。4を初根としてDに立てる。

手順３：4の平方を第1群の23から引く。23-16=07となる。： -a^2

手順４：初根4の2倍8をAに置き、倍根とする。77に注目する。

手順５：77を倍根8で割る。商9を得て、割止める。次根9をEに置く。

手順６：FGの77から倍根8と次根9の積を引く。77-8x9=05をFGに置く。

手順７：9の平方=81を第2群の51から引けないので9は過大根だとわかる。よって次根9から1を引き8をEに置く。そして倍根8を還元して05+08=13をFGに置く。

手順８：次根8とFGHの131に注目する。

手順９：次根8の平方=64をFGHの131から引く。131-64=67をGHに置く。

手順１０：倍根80と次根8に注目する。

手順１１：次根8の2倍(=16)を倍根80に加える。2x8+80=96をABに置く。

手順１２：GHIの676を倍根96で割る。

手順１３：商7を得て、割止め、この商を第3根とする。第3根の7をFに置き、余り676-96x7=004をGHIに置く。

手順１４：第3根7と第3群IJの49に注目する。

手順１５：第3根7の平方=49を第3群の49から引く。49-49=00をIJに置く。

手順１６：根は487と求まる。

最終状態：答 487

珠の状態推移を表にすると次のようになる。（クリックで拡大）

第１３回も引き続き倍根法による開平を行う。

関連記事：

ファインマン v.s. 算盤の達人：ファインマン先生に立方根計算の雪辱を果たそう
http://blog.goo.ne.jp/ktonegaw/e/89a0b907577f03ef6132cf9664bdcddb

ブログ執筆のはげみになりますので、１つずつ応援クリックをお願いします。

↧

クラウド量子計算入門：中山茂：(3) 前回の記事の訂正

April 8, 2017, 10:53 pm

≫ Next: Square root 323,761 using abacus (Double-root method 7)

≪ Previous: 開平と開立（第12回）：237,169の算盤による開平（倍根法６）

またブロッホ測定のアイコンがComposer上に配置できないというのは本当だが、現在の仕様でブロッホ球は測定結果のページに自動的に表示されるようになっている。ただし、本書が書かれていたときの表示方法とは違うので、注意が必要だ。たとえばこの画像のように３つの量子ビットが１つのブロッホ球に表示されるのが現在の仕様だ。

上にあげた２つのスクリーンショットは本書の268ページで説明されている「GHZ状態のZZZ測定」という実験を行った結果だ。

これは多粒子（この場合は３粒子）のもつれ状態であるGHZ状態を用いて量子非局所性状態を証明するための実験である。ベル状態よりもGHZ状態を用いたほうが局所実在性の破れが強く出て、ベル状態の局所実在性の確率論的な破れよりも、GHZ状態の局所実在性のほうが決定論的な破れがあるとされている。

ということで、本書に解説されているすべての実験は現在公開されている量子コンピュータで実験可能であることがわかった。けれども、章ごとにすべて実験して紹介すると１年くらいかかってしまう。であるから、いくつかめぼしい実験を紹介をするにとどめ、本全体の感想記事として後日書かせていただくことにしたい。

著者の中山先生は次の本も2年前にお書きになっている。目次を見ると本書の理論的側面を学べる本だということがわかる。合わせてお読みになるとよいだろう。Kindle版は固定レイアウトなのでご注意。

「量子アルゴリズム：中山茂」（Kindle版）（目次）

量子コンピュータ関連の本： Amazonで検索

関連記事：

発売情報：クラウド量子計算入門：中山茂
http://blog.goo.ne.jp/ktonegaw/e/d360b69100fbe723c5b9410dbf3f5f4d

量子コンピュータ入門：宮野健次郎、古澤明
http://blog.goo.ne.jp/ktonegaw/e/ef75709187cf4b35a12f2d9fdf73a320

ファインマン計算機科学：ファインマン, A.ヘイ, R.アレン
http://blog.goo.ne.jp/ktonegaw/e/4f7f453019fd463ed2bfdeaa7b288d79

量子コンピュータ、量子アルゴリズムを学びたい高校生のために
http://blog.goo.ne.jp/ktonegaw/e/1b2940b648bda682aa27192eb8261972

発売情報：量子プログラミングの基礎：イン・ミンシェン
http://blog.goo.ne.jp/ktonegaw/e/27e4d9a10982d4d69c0029fc4c801708

関連ページ：

IBMの量子コンピュータを使ってみた
http://kadora.hatenablog.com/entry/2016/09/10/230116

従来のPCの1億倍高速な量子コンピューターはどのような仕組みで動いて物理的限界を突破しているのかがわかるムービー
http://gigazine.net/news/20151210-quantum-computers-explained/

わかりやすい量子コンピュータ
http://matome.naver.jp/odai/2133630808407668301

「ITエンジニアのための量子コンピュータ入門」連載一覧
http://codezine.jp/article/corner/629

量子力学の反常識が創りだす量子コンピューティングの世界
?量子コンピュータの頭脳としての量子アルゴリズム?
http://www.kyoto-su.ac.jp/project/st/st14_03.html

米メリーランド大学、世界初となる「汎用計算可能量子コンピュータ」モジュールを開発
http://pc.watch.impress.co.jp/docs/news/1014034.html

関連動画：

量子論、量子テレポーテーション、量子コンピュータ

量子の制御とコンピュータ（量子コンピュータの原理の概要説明）

量子コンピュータ授業 #1（15回の講義。本書で解説される量子ゲート、量子アルゴリズムのほとんどを学ぶことができる。）

15回の講義内容

ブログ執筆のはげみになりますので、１つずつ応援クリックをお願いします。

「クラウド量子計算入門―IBMの量子シミュレーションと量子コンピュータ：中山茂」

↧

Square root 323,761 using abacus (Double-root method 7)

April 15, 2017, 3:06 am

≫ Next: 開平と開立（第13回）：323,761の算盤による開平（倍根法７）

≪ Previous: クラウド量子計算入門：中山茂：(3) 前回の記事の訂正

[Set 323,761 on Mr. Square root]Zoom

[Japanese]

We will continue from where we ended in the last article, the article shows actual solutions to calculate Square root using abacus. Today's example is simple - basic Double-root method, root is 3-digits case. We require 9 as root in the middle of calculation. Please check the Theory page for your reference.

Square root methods: Double-root method, Double-root alternative method, half-multiplication table method, half-multiplication table alternative method, multiplication-subtraction method, constant number method, etc.

Abacus steps to solve Square root of 323,761
(Answer is 569)

"1st group number" is the left most numbers in the 2-digits groups of the given number for square root calculation. Number of groups is the number of digits of the Square root.

323761 -> (32|37|61) : 32 is the 1st group number. The root digits is 3.

Step 1: Set 323761. 1st group is 32.。

Step 2: Square number smaller than or equal to 32 is 25=5^2. 5 is the 1st root.

Step 3: Subtract 5^2 from the 1st group 32. 32-25=07

Step 4: Place 10 which is 2x of 1st root 5. This 10 is double root. Focus on 73.

Step 5: Divide 73 by 10. Answer=6 and this is 2nd root. Subtract 10x6 from 73. 73-10x6=13

Step 6: Place 2x double root 12 on BC. Focus on 37.

Step 7: Subtract 6^2 from 37. 37-6x6=01。

Step 8: Focus on 2nd root 8 and 131 on FGH.

Step 9: Divide 1016 by 12. Answer=9. 9 is the 3rd root on G.

Step 10: Set 1016-112x9=0008 on HIJK.

Step 11: Focus on 3rd root 9 and 81 on KL.

Step 12: Subtract 9^2 from 81 on KL. Set 81-81=00 on KL.

Step 13: Square root of 323761 is 569.

Final state: Answer 569

Abacus state transition. (Click to Zoom)

↧

開平と開立（第13回）：323,761の算盤による開平（倍根法７）

April 15, 2017, 3:09 am

≫ Next: 発売情報：ファインマン物理学問題集 1、2

≪ Previous: Square root 323,761 using abacus (Double-root method 7)

「開平はん」に323,761を置いたところ拡大

[English]

前回に続き、算盤での開平の手順を解説する。今回も倍根法で、根が3桁、途中で9を立根する場合だ。理論編も参考にしていただきたい。

開平（平方根）：倍根法(2商法)、倍根法別法、半九九法、半九九法別法、乗減法、定数法(折衷法) 、過大数開平、省略開平など

算盤による323,761の2乗根の解法（答は569）

第１群の数とは平方根を求める数を２桁ずつ区切り、いちばん大きい（いちばん左）の２桁のことである。群の数が根の桁数となる。

323,761 -> (32|37|61) : 32が第１群の数、根の桁数は3

手順１：323761を置く。第1群は32。

手順２：32以下の平方数は25=5x5。5を初根としてEに立てる。

手順３：5の平方を第1群の32から引く。32-25=07となる。

手順４：初根5の2倍10をABに置き、倍根とする。73に注目する。

手順５：73を倍根10で割る。商6を得て、割止める。次根6をFに置く。HIの73から倍根10と次根6の積60を引き13を得る。

手順６：次根6の2倍、12をBCに置く。37に注目する。

手順７：次根6の平方36をIJの37から引く。

手順８：倍根112とHIJKの1016に注目する。

手順９：1016を12で割り、商9を得て割止め、商9を第3根としGに置く。

手順１０：1016-112x9=0008をHIJKに置く。

手順１１：第3根9とKLの81に注目する。

手順１２：第3根9の平方=81をKLの81から引く。81-81=00をKLに置く。

手順１３：根は569と求まる。

最終状態：答 569

珠の状態推移を表にすると次のようになる。（クリックで拡大）

第１４回も引き続き倍根法による開平を行う。

関連記事：

ファインマン v.s. 算盤の達人：ファインマン先生に立方根計算の雪辱を果たそう
http://blog.goo.ne.jp/ktonegaw/e/89a0b907577f03ef6132cf9664bdcddb

ブログ執筆のはげみになりますので、１つずつ応援クリックをお願いします。

↧

発売情報：ファインマン物理学問題集 1、2

April 15, 2017, 9:44 pm

≫ Next: クラウド量子計算入門：中山茂：(4) 全体の感想

≪ Previous: 開平と開立（第13回）：323,761の算盤による開平（倍根法７）

「ファインマン物理学問題集 1」
「ファインマン物理学問題集 2」

内容紹介：
名著『ファインマン物理学』に完全準拠する初の問題集。ファインマン自身が講義した当時の演習問題を再現し、ほとんどの問題に解答を付した。
『問題集1』は、主として『ファインマン物理学』のI、II巻に対応して、力学、光・熱・波動を扱う。
『問題集2』は、主として『ファインマン物理学』のIII～V巻に対応して、電磁気学、電磁波と物性、量子力学を扱う。学習者の為に、日本語版独自の「ヒントと略解」を加えた。
学習者のために標準的な問題に限って、日本語版独自の「ヒントと略解」を加えた。
2017年4月12日刊行、208ページ、160ページ。

著者について：
R.P.ファインマン（Richard P. Feynman：1918-1988）: ウィキペディアの記事　HP: www.feynman.com
1918‐1988。ニューヨーク市に生まれる。1939年マサチューセッツ工科大学卒業。プリンストン大学大学院に学び、1942年博士号を取得。その後、原爆開発のマンハッタン計画に参加。1945‐50年コーネル大学助教授。1950年以後はカリフォルニア工科大学教授。1965年、量子電気力学の構成の業績で、シュヴィンガー、朝永振一郎と共にノーベル物理学賞を受賞。学部学生向けの教科書「ファインマン物理学」シリーズ(岩波書店)や、『ファインマン統計力学』(シュプリンガー・ジャパン)をはじめとする独創的で魅力溢れる物理学書は世界中で読まれている。『物理法則はいかにして発見されたか』(ダイヤモンド社、のち岩波現代文庫)、『光と物質のふしぎな理論──私の量子電磁力学』『ご冗談でしょう、ファインマンさん──ノーベル賞物理学者の自伝』(いずれも岩波書店)などの著作も多くの読者に親しまれている。

訳者について：
河辺哲次（かわべ　てつじ）
九州大学名誉教授。1949年福岡市生まれ。東北大学工学部原子核工学科卒。九州大学大学院理学研究科博士課程修了（理学博士）。その後、高エネルギー物理学研究所（KEK）助手、九州芸術工科大学教授、九州大学大学院教授を務める。この間、コペンハーゲン大学ニールス・ボーア研究所に留学。専門は素粒子論、場の理論におけるカオス現象、非線形振動・波動現象。著書に『スタンダード力学』『ベーシック電磁気学』『工科系のための解析力学』『物理と工学のベーシック数学』（以上、裳華房）ほか、訳書に『マクスウェル方程式』『物理のためのベクトルとテンソル』『算数でわかる天文学』『波動力学・電磁気学・量子力学』（以上、岩波書店）、『量子論の果てなき境界』（共立出版）。

ファインマン先生の生誕100年（没後としては30年）を来年に控え、待望の問題集が岩波書店から発売された。みすず書房も「【新版】量子力学と経路積分：R.P.ファインマン、A.R.ヒッブス」を先月出したばかりである。今年から来年にかけてファインマン先生関連本の出版ラッシュになるのかもしれない。

来年は生誕100周年記念版として赤い表紙のハードカバーで日本語版を復刻してほしいものだ。

また、ニュートンムック（別冊Newton）は物理学、数学、宇宙関連、その他の自然科学に分けて刊行されているが、いっそ科学者、数学者の伝記シリーズとしてファインマン先生を第一弾で取り上げてみてはいかがだろうか？経営再建を目指すニュートンプレスさんへの提案である。

今回発売されたのはこの２冊。すでに書店に並んでいる。

「ファインマン物理学問題集 1」
「ファインマン物理学問題集 2」

翻訳のもとになった英語版は2014年に刊行されたこの本だ。ちなみにフランス語版は2015年3月に刊行されている。（参考記事：「発売情報：フランス語版「ファインマン物理学」の新版」）

「Exercises for the Feynman Lectures on Physics (2014)」（発売情報記事）

1961年から1963年にかけて行われたファインマン先生の講義は教科書を使わずに行われた。その代わりに講義を受講した学生や先生によって講義資料が急ピッチで作成された。この貴重な資料は現在ネット公開されていて、講義の要約、実験の手順、実験の説明、宿題、試験やクイズから構成されている。宿題や試験の解答は含まれていない。今回発売された演習問題集のルーツはこれらの資料ということになる。

The Feynman Lectures on Physics - Original Course Handouts
http://www.feynmanlectures.info/FLP_Original_Course_Notes/

すでに刊行済みのテキストや別冊本はこちらだ。

「ファインマン物理学 I 力学」(1986)
「ファインマン物理学 II 光・熱・波動」(1986)
「ファインマン物理学 III 電磁気学」(1986)
「ファインマン物理学 IV 電磁波と物性〔増補版〕」(2002)
「ファインマン物理学 V 量子力学」(1986)

「ファインマン流物理がわかるコツ増補版：リチャード・P.ファインマン」（発売情報記事）

以下は有名な動画。YouTubeだと英語字幕を表示できるが、日本語字幕が必要な方はオリジナルのサイトでご覧になるとよい。

レナード・サスキンド：友人リチャード・ファインマン

その他のファインマン先生の動画はこちらのリンク集からご覧いただける。

Richard Feynman videos
http://www.richard-feynman.net/videos.htm

関連記事：

ファインマン先生の自伝本と講演本
http://blog.goo.ne.jp/ktonegaw/e/9bf47cf51085c74caf34a11068a17285

ファインマン物理学（英語版）が全巻ネット公開されました。
http://blog.goo.ne.jp/ktonegaw/e/e94dd49d7d8cc395e29d37927e30173d

The Feynman Lectures on Physics: The New Millennium Edition
http://blog.goo.ne.jp/ktonegaw/e/cb58141ade509fb63952d49ef57c70c7

発売情報： Exercises for the Feynman Lectures on Physics
http://blog.goo.ne.jp/ktonegaw/e/03397d514b604c07f24f484a6663fc1a

ファインマン物理学：英語版とフランス語版
http://blog.goo.ne.jp/ktonegaw/e/1dbcd1e1b02616ef1363ced99a912072

発売情報：フランス語版「ファインマン物理学」の新版
http://blog.goo.ne.jp/ktonegaw/e/daf630deb00e6c315897d6f47ba3dd5a

発売情報：ファインマン流物理がわかるコツ増補版：リチャード・P.ファインマン
http://blog.goo.ne.jp/ktonegaw/e/83a568c20b540ef2a55bed0d7929dcc2

ファインマン計算機科学：ファインマン, A.ヘイ, R.アレン
http://blog.goo.ne.jp/ktonegaw/e/4f7f453019fd463ed2bfdeaa7b288d79

開平と開立（第５回）：ファインマン先生に立方根計算の雪辱を果たそう
http://blog.goo.ne.jp/ktonegaw/e/89a0b907577f03ef6132cf9664bdcddb

ブログ執筆のはげみになりますので、１つずつ応援クリックをお願いします。

「ファインマン物理学問題集 1」
「ファインマン物理学問題集 2」

序文
I
第１章　動くアトム
第２章　エネルギーの保存
第３章　万有引力の理論
第４章　運　動
第５章　ニュートンの力学法則
第６章　運動量の保存
第７章　ベクトル
第８章　非相対論的な2体衝突問題
第９章　力の性質
第10章　ポテンシャルと場
第11章　単位と次元
第12章　特殊相対性理論
第13章　相対論的エネルギーと運動量
第14章　2次元の回転質量中心
第15章　角運動量慣性モーメント
第16章　3次元空間における回転
第17章　調和振動子と線形微分方程式
第18章　代　数
第19章　減衰のある強制振動
第20章　幾何光学
第21章　電磁放射――干渉
第22章　電磁放射――回折
第23章　電磁放射――屈折，分散，吸収
第24章　電磁放射――放射減衰，散乱
第25章　電磁放射偏光
第26章　電磁放射相対論的効果
第27章　量子の振る舞い――波，粒子，光子
第28章　気体分子運動論
第29章　統計力学の原理
第30章　運動論の応用等分配則
第31章　運動論の応用輸送現象
第32章　熱力学
第33章　熱力学の説明
第34章　波動方程式，音
第35章　線形な系うなり，モード
第36章　波のフーリエ解析

付録A　単位と次元
付録B　物理定数と（丸め）値
解答
標準的な問題を解くためのヒントと略解（河辺哲次）
訳者あとがき

II
第37章　電磁気学
第38章　ベクトル場の微分法
第39章　ベクトル場の積分法
第40章　静電気
第41章　ガウスの法則の応用
第42章　さまざまな状況での電場
第43章　さまざまな状況での電場（続き）
第44章　静電エネルギー
第45章　誘電体
第46章　誘電体の内部
第47章　静電アナログ
第48章　静磁場
第49章　さまざまな条件下での磁場
第50章　ベクトルポテンシャル
第51章　電磁誘導の法則
第52章　自由空間でのマクスウェル方程式の解
第53章　電流と電荷のある場合のマクスウェル方程式の解
第54章　AC回路
第55章　空洞共振器
第56章　導波管
第57章　電磁気学の相対論的記述
第58章　場のローレンツ変換
第59章　場のエネルギーと場の運動量
第60章　電磁的な質量
第61章　電磁場内での電荷の運動
第62章　密な物質の屈折率
第63章　表面反射
第64章　物質の磁性
第65章　常磁性と磁気共鳴
第66章　磁性体
第67章　弾性体
第68章　粘性のない流れ
第69章　粘性のある流れ
　
III
第70章　確率振幅
第71章　同種粒子
第72章　スピン1
第73章　スピン1/2
第74章　振幅の時間依存性
第75章　ハミルトニアン行列
第76章　アンモニア・メーザー
第77章　他の2状態系
第78章　さらに2状態系について
第79章　水素原子の超微細構造
第80章　結晶格子内における伝播
第81章　半導体
第82章　独立粒子近似
第83章　振幅の位置依存性
第84章　角運動量
第85章　水素原子と周期表

付録A　単位と次元
付録B　物理定数と（丸め）値
解答
標準的な問題を解くためのヒントと略解（河辺哲次）
訳者あとがき

↧

クラウド量子計算入門：中山茂：(4) 全体の感想

April 22, 2017, 4:18 am

≫ Next: ラジオ談義３：外国語講座、ラジオドラマなど

≪ Previous: 発売情報：ファインマン物理学問題集 1、2

「クラウド量子計算入門―IBMの量子シミュレーションと量子コンピュータ：中山茂」

内容紹介：
IBMから提供される無料の量子計算プラットフォームを体験する!大学での講義を想定した豊富な例題、演習、実験で理解を深める。16の量子実験を通して、量子アルゴリズムを学び、量子シミュレーションで実行する。
2016年10月10日刊行、331ページ。

著者について：
中山茂（なかやましげる）
京都生まれ。京都大学大学院工学研究科博士課程修了後、上智大学、英国Reading大学、京都工芸繊維大学、兵庫教育大学、英国Oxford大学、鹿児島大学を経て、2014年に定年退職。京都大学工学博士。

理数系書籍のレビュー記事は本書で329冊目。

IBM Quantum Experience（入口）
http://www.research.ibm.com/quantum/

その後、ヒマを見つけては本書を頼りに量子コンピュータで実験を繰り返していた。うまくいく実験もあれば、できない実験もあった。行列とケット・ベクトルの計算もできるようになったし、章別に紹介されているアルゴリズムも理解できた。当初の目的は果たせたのだと思う。

さて、紹介記事を書く段になって困ってしまった。いくつも実験をしたのでどれを取り上げて紹介したらよいか迷うのだ。全部紹介するのはもちろん無理で、かといって本の真ん中あたりのアルゴリズムを紹介するのも難しい。章を追うごとに前の章の結果を使った形で次のアルゴリズムが紹介されているからだ。途中の章をいきなり紹介したところでブログの読者には何のことかわからなくなる。

しばらく考えて思いついたのが「量子現象の基礎的な原理を象徴的に示している実験」に限定して紹介するということだ。量子アルゴリズムにも興味があるが、自然科学の基本原理により強い興味を持っている僕には「萌え度」が高まるからだ。

つまり「基本的な量子ゲートの紹介」、「量子の絡み合い（エンタングルメント）」、「量子テレポーテーション」の３つをこの記事で紹介することにした。基本的な量子ゲートのひとつ「アダマールゲート」が生成する量子の重ね合わせ、そして「トフォリゲート」が可能にする量子の絡み合いの２つが古典コンピュータにはない利点を量子コンピュータに与えている原理なのである。

差し当たり本書の章立てはこうなっている。

第1章　はじめてのIBMの5量子ビット実験
第2章　パウリゲートの量子実験
第3章　アダマールゲートの量子実験
第4章　位相シフトゲートの量子実験
第5章　制御NOTゲートの量子実験
第6章　トフォリゲートの量子実験
第7章　ドイチ・ジョザ問題の量子実験
第8章　ベルンシュタイン・ヴァジラニ問題の量子実験
第9章　サイモン問題の量子実験
第10章　量子フーリエ変換の量子実験
第11章　位相・固有値・位数推定問題の量子実験
第12章　ショアの素因数分解問題の量子実験
第13章　グローバーの探索問題の量子実験
第14章　量子非局所性の量子実験
第15章　量子通信の量子実験
第16章　量子エラーとスタビライザー測定
第17章　量子誤り訂正の量子実験

第6章までは基本的な量子ゲートの解説と実験にあてられている。そして第7章から第17章までは量子アルゴリズムの解説と実験だ。

古典コンピュータではANDゲート、ORゲート、NOTゲート、NORゲートなどが用意されていて、これらを組み合わせて論理回路を構成する。原理的にはANDゲートとNOTゲートだけ、あるいはNORゲートだけを使ってあらゆる論理回路を作ることができる。その最小構成を万能ゲートと呼んでいる。

基本的な量子ゲート

量子コンピュータにも万能ゲートを考えることができるわけだが、公開されているIBMの量子コンピュータでは次のようなゲートが用意されている。

グループ別に紹介しよう。

まず、恒等演算を行うidゲート、そしてX、Y、Zであらわされるパウリゲートだ。

たとえば状態0や状態1を表すケット・ベクトルに対してXやZの演算を行うと演算後の状態ベクトルは次のように計算される。ちなみにXゲートが古典コンピュータのNOTゲートに対応している。

Hゲートはアダマールゲートと呼ばれ、「重ね合わせ状態」を作るために使われる。行列では次のようにあらわされる。量子コンピュータが現在のスパコンをはるかに凌ぐ速度で計算できるのも量子の重ね合わせ状態を使うからである。

SとTそしてそれらにタガーがついたものは位相シフトゲートと呼ばれ、次のような行列であらわされる。

そして〇の中に十字が描かれたアイコンであらわされるのが制御NOTゲートだ。CNOTゲートと書かれることもある。このゲートを使うと「絡み合い状態」を作ることができる。本書では絡み合い状態のことを「もつれ状態」と呼んでいる。量子通信（つまり量子テレポーテーション）はこのゲートを使って実現される。

第6章で紹介されるトフォリゲートは制御NOTゲートを２つ使って構成する「制御制御NOTゲート（CCNOTゲート）」のことである。制御NOTゲートが2粒子の絡み合い状態を作るのに対し、トフォリゲートでは3粒子の絡み合い状態を作ることができる。そしてゲートを増やせば多粒子の絡み合い状態を作れる。

実験１：量子の絡み合い

この実験は前回の記事で紹介した。本書の第14章「量子非局所性の量子実験」で説明されている「GHZ状態のZZZ測定」という実験のことだ。

これは多粒子（この場合は３粒子）の絡み合い状態である「GHZ状態」を用いて量子非局所性状態を証明するための実験だ。２粒子系の「ベル状態」よりも３粒子系の「GHZ状態」を用いたほうが局所実在性の破れが強く出て、ベル状態の局所実在性の確率論的な破れよりも、GHZ状態の局所実在性のほうが決定論的な破れがあるとされている。

この実験でアインシュタインが「不可解な遠隔作用」、「EPRパラドックス」として忌み嫌った状況が量子コンピュータ内に再現できたことになる。

量子回路（アルゴリズム）：第6章で解説されているトフォリゲートが使われている。

実験結果（クリックで拡大）

実験２：量子テレポーテーション

そもそもこのブログが物理ブログになったのは量子テレポーテーションの実験が成功していることに衝撃を受けたのがきっかけだ。本書の第15章「量子通信の量子実験」とは量子テレポーテーション、量子転送のことである。（参考記事：「テレポーテーションは実現している。（リンク集）」）

IBMの量子コンピュータでは状態0、状態1のようなシンプルな状態の量子転送（つまり通常の意味での量子テレポーテーション）だけでなく、重ね合わせ状態の量子転送や絡み合い状態の量子転送を行うことができる。
　
ここでは重ね合わせ状態の量子転送実験を紹介しよう。

転送するのはXゲートとHゲートを使って生成した重ね合わせ状態だ。

つまり量子ビット0にあるこの状態を転送することになる。

そのまま測定すると、このように量子ビット0は状態0と状態1が半々の重ね合わせの状態であることがわかる。棒グラフの下の5つの数字のいちばん右が量子ビット0である。

量子ビット0の重ね合わせ状態を量子ビット2に転送するのがこの実験だ。

量子転送では量子の絡み合いを利用するから量子転送ゲートの中にトフォリゲートがあるのがおわかりいただけるだろう。赤枠で囲った部分が量子転送ゲートである。測定アイコンは量子ビット2の量子転送ゲートの後ろに置く。

量子回路（アルゴリズム）

実験結果

量子ビット2（5つ並んでいる数字の右から3番目）がもとの量子状態と同じく状態0と状態1が半々の重ね合わせの状態であることがわかるだろう。つまり重ね合わせ状態の転送に成功したことがわかるのだ。量子ビット0から量子ビット2へのほんのわずかな距離の量子テレポーテーションである。

5つの量子ビットが搭載されたIBMの量子コンピュータ心臓部

その他の感想、考えたこと

ファインマン先生は著書「ファインマン計算機科学：ファインマン, A.ヘイ, R.アレン」で量子コンピュータのアイデアを公表したが、それは原子サイズの素子を使ったコンピュータ、可逆計算ができるコンピュータという意味においてである。重ね合わせ状態を使った超超高速並列計算に関して言えばファインマン先生は気が付いていなかった。この点において量子コンピュータの本当の発案者はドイチェ・ジョザのアルゴリズムを考案者のうちのひとり、ドイチェである。

量子アルゴリズムの研究は始まったばかりだ。本書には「古典コンピュータのアルゴリズムのすべてが量子コンピュータで実現できるわけではない。」と書かれている。汎用量子コンピュータができるかどうかは原理的な問題なのか、研究を続ければ実現可能なのかは僕にはわからないが、後者であることを願いたい。「量子プログラミングの基礎：イン・ミンシェン」という本が出たばかりだが、現在のコンピュータのようにプログラミング言語を使って自在に開発を行えるような量子コンピュータが実現するのはもう少し先のようである。

量子アルゴリズムは本書を読みながらやっと理解できた。自分でアルゴリズムを考え量子ゲートを組み上げることはできないことを実感した。僕は古典コンピュータの論理ゲートを使ったデジタル回路さえ作ったことがないのだから、当然と言えば当然である。（参考記事：「電卓を作りたいという妄想」）

また、IBMの量子コンピュータで公開されているUser Guideだけ読んで量子アルゴリズムの実験をして遊ぶのも初心者には無理だ。専門書で学ぶか本書のような解説本を参照しながらであれば、高校生でも実験を楽しむことができる。ぜひ、ご自身で試してみてほしい。

ブログを始めて12年。現実の世界、ニューヨークに置かれた量子コンピュータを使って僕はようやく自分で量子テレポーテーションの実験を行なったことになる。小さいながらも今日は記念日だ。

著者の中山先生は次の本も2年前にお書きになっている。目次を見ると本書の理論的側面を学べる本だということがわかる。合わせてお読みになるとよいだろう。Kindle版は固定レイアウトなのでご注意。

「量子アルゴリズム：中山茂」（Kindle版）（目次）

量子コンピュータ関連の本： Amazonで検索

関連記事：

発売情報：クラウド量子計算入門：中山茂
http://blog.goo.ne.jp/ktonegaw/e/d360b69100fbe723c5b9410dbf3f5f4d

量子コンピュータ入門：宮野健次郎、古澤明
http://blog.goo.ne.jp/ktonegaw/e/ef75709187cf4b35a12f2d9fdf73a320

ファインマン計算機科学：ファインマン, A.ヘイ, R.アレン
http://blog.goo.ne.jp/ktonegaw/e/4f7f453019fd463ed2bfdeaa7b288d79

量子コンピュータ、量子アルゴリズムを学びたい高校生のために
http://blog.goo.ne.jp/ktonegaw/e/1b2940b648bda682aa27192eb8261972

発売情報：量子プログラミングの基礎：イン・ミンシェン
http://blog.goo.ne.jp/ktonegaw/e/27e4d9a10982d4d69c0029fc4c801708

関連ページ：

IBMの量子コンピュータを使ってみた
http://kadora.hatenablog.com/entry/2016/09/10/230116

従来のPCの1億倍高速な量子コンピューターはどのような仕組みで動いて物理的限界を突破しているのかがわかるムービー
http://gigazine.net/news/20151210-quantum-computers-explained/

わかりやすい量子コンピュータ
http://matome.naver.jp/odai/2133630808407668301

「ITエンジニアのための量子コンピュータ入門」連載一覧
http://codezine.jp/article/corner/629

量子力学の反常識が創りだす量子コンピューティングの世界
～量子コンピュータの頭脳としての量子アルゴリズム～
http://www.kyoto-su.ac.jp/project/st/st14_03.html

米メリーランド大学、世界初となる「汎用計算可能量子コンピュータ」モジュールを開発
http://pc.watch.impress.co.jp/docs/news/1014034.html

関連動画：

量子論、量子テレポーテーション、量子コンピュータ

量子の制御とコンピュータ（量子コンピュータの原理の概要説明）

量子コンピュータ授業 #1（15回の講義。本書で解説される量子ゲート、量子アルゴリズムのほとんどを学ぶことができる。）

15回の講義内容

ブログ執筆のはげみになりますので、１つずつ応援クリックをお願いします。

「クラウド量子計算入門―IBMの量子シミュレーションと量子コンピュータ：中山茂」

↧

ラジオ談義３：外国語講座、ラジオドラマなど

April 24, 2017, 8:52 pm

≫ Next: Square root 164,836 using abacus (Double-root method 8)

≪ Previous: クラウド量子計算入門：中山茂：(4) 全体の感想

前回の記事で紹介した「Radikool」は大活躍している。４月になりNHKの外国語会話の放送が始まったので通勤時間に聞いている。この他にもふだん聞いている番組を紹介しておこう。

まいにち中国語、まいにちロシア語（入門編）

まいにち中国語
https://cgi2.nhk.or.jp/gogaku/chinese/kouza/

まいにちロシア語（入門編）
https://cgi2.nhk.or.jp/gogaku/russian/kouza/

いまのところ毎日聞けている。この２つは通勤時に駅までの15分間の徒歩を利用。行きと帰りでちょうど１日分だ。購入したKindle版のテキストをスマホでチラ見しながら歩いている。住宅街なので車はほとんど通らない。

中国語は1990年代前半に少しだけ友達から教えてもらっていたし、ロシア語は大学３年のときに第３外国語として授業を受けていたのでもともと馴染みがある。

中国語のほうは月曜から金曜まで週５回、ロシア語の基礎編は月曜から水曜までの週３回である。こういうこつこつ毎日聞く番組を継続しやすい性格なのでありがたい。

それぞれ辞書を買おうかと思ったが、辞書を引いている時間がとれない。それに無料辞書が公開されているから、今のところこれで用は足りそうである。便利な時代だ。

中国語オンライン辞書まとめ
http://start-chugoku.com/diconline/

ロシア語辞書
http://cblle.tufs.ac.jp/dic/ru/

ロシア語日本語辞書オンライン
https://ja.glosbe.com/ru/ja

ロシア語エキサイト翻訳
http://www.excite.co.jp/world/russian/

米朝開戦が危惧される昨今だが、奇しくも開戦反対の働きかけや仲裁ができそうな２つの国の言語を選んでいることに後から気がついた。もちろん僕の今のレベルは自己紹介や挨拶をしたりする程度なのだが。

あとは毎晩ウォーキングしながら英語ニュースを聞いたり、実践ビジネス英語、ラジオ英会話などを聞いている。フランス語講座応用編は自分のレベルよりだいぶ低いので、とりあえず今回はお休み。

NHKオーディオドラマ

NHKオーディオドラマ
http://www.nhk.or.jp/audio/

NHKのラジオドラマもいくつかの種類が放送されている。最近放送されたのでハマったのは青春アドベンチャーの「つばき、時跳び」。とてもよかったので原作のKindle本も買ってしまった。昨日から「エイレーネーの瞳シンドバッド23世の冒険（再）（全10回）」が放送されている。再放送なのできっと評判がよかったのだろう。

つばき、時跳び青春アドベンチャー
http://www.nhk.or.jp/audio/html_se/se2017005.html

ここから聞けるようだ。（全話: スマホからだとリンクエラーになるので「つばき　時跳び」の文字列で検索してください。）
http://www.dailymotion.com/video/x5duwtn

Peace of Mind 土曜の朝のサラ・オレイン

いい番組を見つけた！なぜ、これまで気がつかなかったのだろう？早起きはできないから、僕にとっては「土曜の午後のサラ・オレイン」だ。サラさんはEテレの「おとなの基礎英語」にもレギュラー出演されている。

Peace of Mind 土曜の朝のサラ・オレイン
http://www.tfm.co.jp/peace/

こんな感じの番組である。

Peace Of Mind SarahAlainn 2015 5 23 part2

動画を２つだけ紹介するが説明の必要はないだろう。

サラ・オレイン『ANIMA』収録曲「Animus」

サラ・オレイン「Little Doll」

続きは：ミックスリストで再生

壇蜜さんのラジオ番組

「あなたのお耳の愛人壇蜜です…」この言葉で始まる官能的な夜のしゃべり場「壇蜜の耳蜜」。お気に入りである。ｗ

壇蜜の耳蜜： http://radioupdate.net/category/joqr/mitsu/

放送は毎週月曜日 19:30 - 20:00 だ。画像の放送時間は過去のものと思われる。

NHK高校講座（保健体育）： http://www.nhk.or.jp/kokokoza/radio/r2_hoken/

YouTubeからは「壇蜜の耳蜜で検索する」と聴けるようである。直近の放送回はradiko.jpのタイムシフリー機能で聴ける。

NHK高校講座（保健体育）は番組のホームページから聞けるようになっている。

関連記事：

ラジオ談義
http://blog.goo.ne.jp/ktonegaw/e/5196ea330c001a2b803f632a0d1f8456

ラジオ談義２： Radikoolによるラジオ放送の予約録音など
http://blog.goo.ne.jp/ktonegaw/e/d7fa18444e35592f468d01c360742c2e

関連ページ：

ラジオ番組表：ＡＭ　ＦＭ　

ラジオドラマ： NHK FMのオーディオドラマ

お勧め：地下鉄のアリス（1978年放送のFMラジオドラマ、脚本は別役実）

NHKゴガク： https://www2.nhk.or.jp/gogaku/

ブログ執筆のはげみになりますので、１つずつ応援クリックをお願いします。

↧

Square root 164,836 using abacus (Double-root method 8)

April 26, 2017, 8:02 am

≫ Next: 開平と開立（第14回）：164,836の算盤による開平（倍根法８）

≪ Previous: ラジオ談義３：外国語講座、ラジオドラマなど

[Set 164,836 on Mr. Square root]Zoom

[Japanese]

We will continue from where we ended in the last article, the article shows actual solutions to calculate Square root using abacus. Today's example is simple - basic Double-root method, root is 3-digits case. There is Zero in root. Please check the Theory page for your reference.

Square root methods: Double-root method, Double-root alternative method, half-multiplication table method, half-multiplication table alternative method, multiplication-subtraction method, constant number method, etc.

Abacus steps to solve Square root of 164,836
(Answer is 406)

"1st group number" is the left most numbers in the 2-digits groups of the given number for square root calculation. Number of groups is the number of digits of the Square root.

164836 -> (16|48|36) : 16 is the 1st group number. The root digits is 3.

Step 1: Set 164836. 1st group is 16.

Step 2: Square number smaller than or equal to 16 is 16=4^2. 4 is the 1st root.

Step 3: Subtract 4^2 from the 1st group 16. 16-16=00

Step 4: Place 8 which is 2x of 1st root 4. This 8 is double root. Focus on 48.

Step 5: Cannot divide 04 by 8. Place 0 on E as 2nd root.

Step 6: Divide 483 by double root 80.

Step 7: Answer is 6 and this is 3rd root.

Step 8: Place 483-80x6=003 on GHI.

Step 9: Subtract square of 3rd root 6 from 36 on IJ.

Step 10: Place 36-6x6=00 on IJ.

Step 11: Square root of 164836 is 406.

Final state: Answer 406

Abacus state transition. (Click to Zoom)

↧

開平と開立（第14回）：164,836の算盤による開平（倍根法８）

April 26, 2017, 8:03 am

≫ Next: 量子コンピュータ―超並列計算のからくり：竹内繁樹

≪ Previous: Square root 164,836 using abacus (Double-root method 8)

「開平はん」に164,836を置いたところ拡大

[English]

前回に続き、算盤での開平の手順を解説する。今回も倍根法で、根が3桁、根に0が含まれる場合だ。理論編も参考にしていただきたい。

開平（平方根）：倍根法(2商法)、倍根法別法、半九九法、半九九法別法、乗減法、定数法(折衷法) 、過大数開平、省略開平など

算盤による164,836の2乗根の解法（答は406）

第１群の数とは平方根を求める数を２桁ずつ区切り、いちばん大きい（いちばん左）の２桁のことである。群の数が根の桁数となる。

164,836 -> (16|48|36) : 16が第１群の数、根の桁数は3

手順１：164836を置く。第1群は16。

手順２：16以下の平方数は16=4x4。4を初根としてDに立てる。

手順３：4の平方を第1群の16から引く。16-16=00となる。

手順４：初根4の2倍8をAに置き、倍根とする。04に注目する。

手順５：FGの04を倍根8で割れないので次根を0とし、Eに置く。

手順６：倍根を80とし、483をこの倍根で割る。

手順７：Fに商6を得て、これを第3根とする。

手順８：483-80x6=003をGHIに置く。

手順９：IJの36から第3根の平方を引く。

手順１０：36-6x6=00をIJに置く。

手順１１：根は406と求まる。

最終状態：答 406

珠の状態推移を表にすると次のようになる。（クリックで拡大）

第１５回も引き続き倍根法による開平を行う。

関連記事：

ファインマン v.s. 算盤の達人：ファインマン先生に立方根計算の雪辱を果たそう
http://blog.goo.ne.jp/ktonegaw/e/89a0b907577f03ef6132cf9664bdcddb

ブログ執筆のはげみになりますので、１つずつ応援クリックをお願いします。

↧