「マイ・コンピュータをつくる―組み立てのテクニック:安田寿明」
内容:
“人工頭脳”とあがめられていたコンピュータが、「マイコン」という、だれもが気軽に使え、持つことができる、じつに楽しい機械となって出現した。
「マイ・コンピュータ入門」の続篇としての本書は、マイ・コンピュータのつくり方の初歩テキストである。どうせ手づくりするなら、本格的なコンピュータが良い。そこで、昭和52年春に開発されたばかりの、最も優秀な性能を有するLSI(大規模集積回路)を利用して、最終的には、大型電子計算機メーカー顔負けの本格的コンピュータを手づくりする方法について、くわしく解説しよう。
著者略歴(1977年、本書出版当時の情報)
安田寿明(やすだ・としあき):昭和10年、兵庫県に生まれる。昭和34年、電気通信大学経営工学科卒業後、読売新聞社に勤務。編集局社会部員、米国特派員、社長直属総合計画室員などを経て、昭和45年退社。現在東京電機大学工学部電気通信工学科助教授。『知識産業』(ダイヤモンド社)などのほか、情報産業、漢字情報処理システム、有線テレビジョンに関する著書、論文が多数ある。
理数系書籍のレビュー記事は本書で226冊目。(マイコンは電子工学系だが広い意味で理系としておく。)
1976年にマイコンキットが登場する4年も前から、自分用のコンピュータを6台も作り上げた著者によるマイコン入門の書。この本によって多くの人がマイコンによって何ができるのかを正しく理解するようになった。未来への夢が生き生きと語られている安田寿明先生が42歳のときにお書きになった「マイ・コンピュータ3部作」の1冊目のレビュー記事。
章立てと大まかな内容は次のとおり。(詳細な目次は記事のいちばん下に書いておいた。)
第1章:ひろがるマイ・コンピュータ時代
1971年に登場したマイクロ・コンピュータには4ビットのものと8ビットものがある。4ビットのものは炊飯器や全自動洗濯機などに組み込むのに適し、それらの電気製品を制御するためのプログラムを焼きこんで大量生産して使われることが多い。それに対し8ビット型は自由にプログラムを書き換える「汎用型」に向いている。マイコンキットは後者のCPUが使われる。
第2章:マイ・コンピュータの基礎
この章ではCPUやメモリーについて基礎的なことが解説される。
世界で初めて開発されたCPUは4ビットのi4004で、すぐ8ビットのi8008が開発された。これらは第一世代のマイクロ・コンピュータである。第二世代はインテル社のi8080やモトローラ社のM6800とされている。
この章ではマイコンの基本3要素(CPU、メモリー、インタフェース)についての説明がなされる。コンピュータはCPUの小型化だけでなく、メモリーやコンピュータ制御システム、周辺機器とのインタフェースなどの回路のLSI化や、それぞれのCPUに対応したメモリー用LSI、インタフェースLSIなどが「ファミリー」として提供され、それらを使うことで小型化が格段に進み「ワンボード・コンピュータ」を作ることが可能になった。第一世代のCPUでコンピュータを作ったときは周辺回路のために12枚ものプリント基板が必要だったのである。
第3章:ワンボードからワンチップ・コンピュータへ
コンピュータの小型化はさらに進む。CPU内にメモリーやインタフェースを組み込んでしまう「コンピュータのワンチップ化」がこの章で解説される。またCPUの動作の基本となる「クロック」の原理が解説される。
次にワンチップ・コンピュータとまではいかなくてもLSIが3個だけで構成されるコンピュータが紹介される。CPUにi8085、256バイトのRAMと3つのインタフェースを備えたi8155、2キロバイトのPROMと2つのインタフェースを備えたi8755という3つのLSIによる構成だ。これはMCS85というコンピュータ・システムの構成例である。
さらにこの章ではこれら3つのLSIを使ってワンボード・マイコンを作るための配線パターンやプリント基板の工作手順が解説される。
第4章:電子ソロバンをつくろう
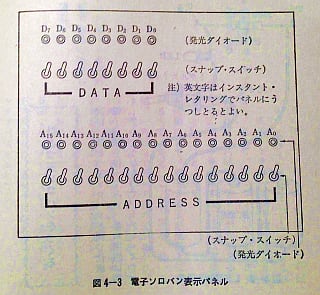
コンピュータの動作原理の基礎、2進法による計算手順を学ぶ。説明には発光ダイオード(LED)を使った「電子ソロバン」が使われる。まず紙の上で2進法の原理を説明し、その後LEDを使った16桁表示パネルとスナップ・スイッチをつないだ回路、安定化電源装置の自作方法が解説される。
2進数16桁の電子ソロバンの表示、入力装置(クリックで拡大)
![]()
第5章:コンピュータ本体をつくる
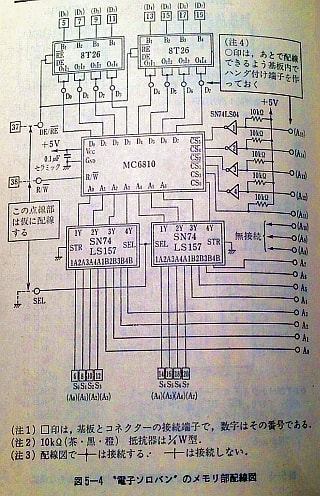
前の章で作った電子ソロバンを使って加算器や減算器を作るのかな?と思っていたら全く違った。次に工作するのはコンピュータのメモリ部なのだ。MOS・LSIを使ってメモリー回路を作る手順が示される。そして次にスナップ・スイッチによる電子ソロバン操作パネルとつなぐためのインタフェース回路の作り方が解説される。そして最後にCPUまわりの回路を作り上げる。CPUはMC6810だ。
これで2進数16桁表示の8ビット・マイコンが完成し、簡単なプログラムを入力して動作確認をする。メモリーはたったの127バイトだが、周辺機器を自在に制御することのできる立派なコンピュータである。マイコンキットを使わずともコンピュータは自作できるのだ。
メモリー回路(クリックで拡大)
![]()
インタフェース回路(クリックで拡大)
![]()
CPUのまわりの回路(クリックで拡大)
![]()
第6章:マイ・コンピュータのいろいろ
せっかく作った自作マイコンも周辺機器とのインタフェースを作るためには知識や時間、そしてお金もかかる。はじめてマイコン制作にチャレンジするのであればキットを買って始めるのがよいだろう。この章では各メーカーから販売されているマイコンキットが紹介される。それぞれ特色があって興味深い。
当時のマイコンキットの性能はCPUクロック2MHz、メモリーは512バイト〜2キロバイト、フロッピーディスクやハードディスクはなく、プログラムやデータの読み書きはカセットテープレコーダが使われていた。
次のようなマイコンキットが写真付きで紹介されている。
- インテル SDK-85(詳細)
- NEC TK-80(詳細)
- モトローラ MEK6800II(詳細)
- 日立 H68/TR(詳細)
- IMSAI-8048(詳細)
- ロジック・システムズ MP-80(詳細)
- NS SC/MPキット(詳細)
- FCI F8キット(詳細)
- インターシル・サンプラー・キット(詳細)
- 東芝 TLCS12A・EX-12/05(詳細)
- パナファコムLKIT/16(詳細)
- その他のマイコン・キット
この章の最後ではアメリカのマイコン事情についても解説している。日本でマイコンキットが発売される2年ほど前の1974年、アメリカでは世界初のホーム・コンピュータALTAIR 8800が発売されブームのきっかけとなった。
ALTAIR 8800 (1974年)、左に少しだけ映っているのはApple I (1976年)
![]()
さらに1977年にはコモドール社がタイプライター型キーボードとキャラクタ表示モニターを備えたPET-2001を発売する。このように個人用コンピュータはプリント基板むき出しの形からスマートな形、使いやすい形に進化していった。パソコンという言葉が定着するのはまだ先のことだが、パソコン時代の幕開けである。
PET 2001 (1977年)
![]()
日本で最初のパソコンNEC PC-8001が発売されるのは本書の出版から2年後の1979年のことである。
NEC PC-8001 (1979年)
![]()
本書は中学3年のときに読んでいたはずだが、覚えていたのは後半、各社から発売されていたマイコンキットの説明の部分だけで、前半はほとんど覚えていなかった。当時はデジタル回路を学んでいなかったので前半を理解できたとは思えない。ただワクワク感は第1作の夢のような話から実際の回路の話になったので「難しい〜。僕にはできそうもない。」と思いながら読んでいたことだろう。
もし本書を読むのであれば前もって「改訂版 電子回路の「しくみ」と「基本」 :小峯龍男」や「改訂版 デジタル回路の「しくみ」と「基本」:小峯龍男」などを読んでおくとよいだろう。
第1作の内容をさらに深く解説し、当時のコンピュータの状況が詳しく読み取れる好書である。コンピュータの原理を学ぶという意味では、現代でも入門用として使えそうな1冊だ。
「マイ・コンピュータ入門―コンピュータはあなたにもつくれる:安田寿明」(リンク2)
「マイ・コンピュータをつくる―組み立てのテクニック:安田寿明」(リンク2)
「マイコンピュータをつかう―周辺機器と活用の実際:安田寿明」
![]()
![]()
![]()
関連記事:
安田寿明先生の「マイ・コンピュータ」3部作(ブルーバックス)
http://blog.goo.ne.jp/ktonegaw/e/e54e4eb38380ff2ff2f51747ca7b4f75
マイ・コンピュータ入門―コンピュータはあなたにもつくれる:安田寿明
http://blog.goo.ne.jp/ktonegaw/e/997e2c40fda774b25ebd5561336a7bfe
NEC TK-80やワンボードマイコンのこと
http://blog.goo.ne.jp/ktonegaw/e/36db2417701c58efa1ac81343e70227b
真空管式コンピュータへのノスタルジア(EDSAC)
http://blog.goo.ne.jp/ktonegaw/e/14c9aeedfcda78c9fd9ff4b677435283
ファインマン計算機科学:ファインマン, A.ヘイ, R.アレン
http://blog.goo.ne.jp/ktonegaw/e/4f7f453019fd463ed2bfdeaa7b288d79
量子コンピュータ入門:宮野健次郎、古澤明
http://blog.goo.ne.jp/ktonegaw/e/ef75709187cf4b35a12f2d9fdf73a320
応援クリックをお願いします!このブログのランキングはこれらのサイトで確認できます。
![にほんブログ村 科学ブログ 物理学へ]()
![人気ブログランキングへ]()
![]()
![]()
「マイ・コンピュータをつくる―組み立てのテクニック:安田寿明」
![]()
まえがき
第1章:ひろがるマイ・コンピュータ時代
- プロローグ/マイクロ・コンピュータの成長性
- マイクロ・コンピュータの種別
- マイコンの主役は4ビット型コンピュータ
- 工場向けの4ビット型/マイ・コンピュータには8ビット以上を
- マイコン・キットの二つの目的/汎用性の8ビット型
- コンピュータ・ホビイストの誕生
第2章:マイ・コンピュータの基礎
- 高級電卓用のi4004/複雑怪奇な手づくり1号機
- i8008のターヘル・アナトミア
- 超小型誇示?のi8008/複雑怪奇なi8008の動作
- 時間分割多重化のしくみ/電極数現象でキャラメル大に
- 小さくしたため周囲は複雑化
- 第二世代マイクロ・コンピュータの誕生
- わずか大学ノート大のコンピュータ
- ワンボード・コンピュータの構成
- プリント基板とは/マイコン・キットの生い立ち
- コンピュータの三要素/インタフェース機能とは
- 「ノイマン・マシン」とは/メモリの効用
- 頭脳の秘密は記憶装置に?/メモリの種別
- 記憶の消失/どれだけ記憶できるか
- ROMとPROM
第3章:ワンボードからワンチップ・コンピュータへ
- 8080型の最小構成
- “脳波発生”のクロック・ジェネレータ
- 動作基準時間の尺度/CPUの動作状態
- システム制御と時間整合/集積回路の区分
- コンピュータかプロセッサか/たった一個でコンピュータ
- 機械のためだけのマイ・コンピュータ
- i8085コンピュータ/i8085の機能
- LSI3個で構成/プリント基板のつくり方
第4章:電子ソロバンをつくろう
- 手足のないダルマ・コンピュータ
- 2進法なんかこわくない/ソロバンは5進/10進法
- ソロバンで練習してみよう/ひとつ玉ソロバンをつくる
- 電源装置のつくり方/電子ソロバンで練習しよう
第5章:コンピュータ本体をつくる
- 事前準備は入念に/配線作業の注意点
- メモリ部の制作/事前の点検整備
- MOS・LSIの装着/メモリの動作チェック
- CPUはMC6802/マイ・コンピュータの構成
- 手づくり向きの1石コンピュータ
第6章:マイ・コンピュータのいろいろ
- 育て上げるには時間と費用が
- メーカー製の組み立てキットもある
- インテル SDK-85
- NEC TK-80
- モトローラ MEK6800II
- 日立 H68/TR
- IMSAI-8048
- ロジック・システムズ MP-80
- NS SC/MPキット
- FCI F8キット
- インターシル・サンプラー・キット
- 東芝 TLCS12A・EX-12/05
- パナファコムLKIT/16
- その他のマイコン・キット
- マイコンからハンサム・コンピュータへ
- 最初のホーム・コンピュータ ALTAIR8800
- アマチュア向けのSWTP
- 動き出した巨大資本
- ホーム・コンピュータへの旅
内容:
“人工頭脳”とあがめられていたコンピュータが、「マイコン」という、だれもが気軽に使え、持つことができる、じつに楽しい機械となって出現した。
「マイ・コンピュータ入門」の続篇としての本書は、マイ・コンピュータのつくり方の初歩テキストである。どうせ手づくりするなら、本格的なコンピュータが良い。そこで、昭和52年春に開発されたばかりの、最も優秀な性能を有するLSI(大規模集積回路)を利用して、最終的には、大型電子計算機メーカー顔負けの本格的コンピュータを手づくりする方法について、くわしく解説しよう。
著者略歴(1977年、本書出版当時の情報)
安田寿明(やすだ・としあき):昭和10年、兵庫県に生まれる。昭和34年、電気通信大学経営工学科卒業後、読売新聞社に勤務。編集局社会部員、米国特派員、社長直属総合計画室員などを経て、昭和45年退社。現在東京電機大学工学部電気通信工学科助教授。『知識産業』(ダイヤモンド社)などのほか、情報産業、漢字情報処理システム、有線テレビジョンに関する著書、論文が多数ある。
理数系書籍のレビュー記事は本書で226冊目。(マイコンは電子工学系だが広い意味で理系としておく。)
1976年にマイコンキットが登場する4年も前から、自分用のコンピュータを6台も作り上げた著者によるマイコン入門の書。この本によって多くの人がマイコンによって何ができるのかを正しく理解するようになった。未来への夢が生き生きと語られている安田寿明先生が42歳のときにお書きになった「マイ・コンピュータ3部作」の1冊目のレビュー記事。
章立てと大まかな内容は次のとおり。(詳細な目次は記事のいちばん下に書いておいた。)
第1章:ひろがるマイ・コンピュータ時代
1971年に登場したマイクロ・コンピュータには4ビットのものと8ビットものがある。4ビットのものは炊飯器や全自動洗濯機などに組み込むのに適し、それらの電気製品を制御するためのプログラムを焼きこんで大量生産して使われることが多い。それに対し8ビット型は自由にプログラムを書き換える「汎用型」に向いている。マイコンキットは後者のCPUが使われる。
第2章:マイ・コンピュータの基礎
この章ではCPUやメモリーについて基礎的なことが解説される。
世界で初めて開発されたCPUは4ビットのi4004で、すぐ8ビットのi8008が開発された。これらは第一世代のマイクロ・コンピュータである。第二世代はインテル社のi8080やモトローラ社のM6800とされている。
この章ではマイコンの基本3要素(CPU、メモリー、インタフェース)についての説明がなされる。コンピュータはCPUの小型化だけでなく、メモリーやコンピュータ制御システム、周辺機器とのインタフェースなどの回路のLSI化や、それぞれのCPUに対応したメモリー用LSI、インタフェースLSIなどが「ファミリー」として提供され、それらを使うことで小型化が格段に進み「ワンボード・コンピュータ」を作ることが可能になった。第一世代のCPUでコンピュータを作ったときは周辺回路のために12枚ものプリント基板が必要だったのである。
第3章:ワンボードからワンチップ・コンピュータへ
コンピュータの小型化はさらに進む。CPU内にメモリーやインタフェースを組み込んでしまう「コンピュータのワンチップ化」がこの章で解説される。またCPUの動作の基本となる「クロック」の原理が解説される。
次にワンチップ・コンピュータとまではいかなくてもLSIが3個だけで構成されるコンピュータが紹介される。CPUにi8085、256バイトのRAMと3つのインタフェースを備えたi8155、2キロバイトのPROMと2つのインタフェースを備えたi8755という3つのLSIによる構成だ。これはMCS85というコンピュータ・システムの構成例である。
さらにこの章ではこれら3つのLSIを使ってワンボード・マイコンを作るための配線パターンやプリント基板の工作手順が解説される。
第4章:電子ソロバンをつくろう
コンピュータの動作原理の基礎、2進法による計算手順を学ぶ。説明には発光ダイオード(LED)を使った「電子ソロバン」が使われる。まず紙の上で2進法の原理を説明し、その後LEDを使った16桁表示パネルとスナップ・スイッチをつないだ回路、安定化電源装置の自作方法が解説される。
2進数16桁の電子ソロバンの表示、入力装置(クリックで拡大)
第5章:コンピュータ本体をつくる
前の章で作った電子ソロバンを使って加算器や減算器を作るのかな?と思っていたら全く違った。次に工作するのはコンピュータのメモリ部なのだ。MOS・LSIを使ってメモリー回路を作る手順が示される。そして次にスナップ・スイッチによる電子ソロバン操作パネルとつなぐためのインタフェース回路の作り方が解説される。そして最後にCPUまわりの回路を作り上げる。CPUはMC6810だ。
これで2進数16桁表示の8ビット・マイコンが完成し、簡単なプログラムを入力して動作確認をする。メモリーはたったの127バイトだが、周辺機器を自在に制御することのできる立派なコンピュータである。マイコンキットを使わずともコンピュータは自作できるのだ。
メモリー回路(クリックで拡大)
インタフェース回路(クリックで拡大)

CPUのまわりの回路(クリックで拡大)

第6章:マイ・コンピュータのいろいろ
せっかく作った自作マイコンも周辺機器とのインタフェースを作るためには知識や時間、そしてお金もかかる。はじめてマイコン制作にチャレンジするのであればキットを買って始めるのがよいだろう。この章では各メーカーから販売されているマイコンキットが紹介される。それぞれ特色があって興味深い。
当時のマイコンキットの性能はCPUクロック2MHz、メモリーは512バイト〜2キロバイト、フロッピーディスクやハードディスクはなく、プログラムやデータの読み書きはカセットテープレコーダが使われていた。
次のようなマイコンキットが写真付きで紹介されている。
- インテル SDK-85(詳細)
- NEC TK-80(詳細)
- モトローラ MEK6800II(詳細)
- 日立 H68/TR(詳細)
- IMSAI-8048(詳細)
- ロジック・システムズ MP-80(詳細)
- NS SC/MPキット(詳細)
- FCI F8キット(詳細)
- インターシル・サンプラー・キット(詳細)
- 東芝 TLCS12A・EX-12/05(詳細)
- パナファコムLKIT/16(詳細)
- その他のマイコン・キット
この章の最後ではアメリカのマイコン事情についても解説している。日本でマイコンキットが発売される2年ほど前の1974年、アメリカでは世界初のホーム・コンピュータALTAIR 8800が発売されブームのきっかけとなった。
ALTAIR 8800 (1974年)、左に少しだけ映っているのはApple I (1976年)

さらに1977年にはコモドール社がタイプライター型キーボードとキャラクタ表示モニターを備えたPET-2001を発売する。このように個人用コンピュータはプリント基板むき出しの形からスマートな形、使いやすい形に進化していった。パソコンという言葉が定着するのはまだ先のことだが、パソコン時代の幕開けである。
PET 2001 (1977年)

日本で最初のパソコンNEC PC-8001が発売されるのは本書の出版から2年後の1979年のことである。
NEC PC-8001 (1979年)

本書は中学3年のときに読んでいたはずだが、覚えていたのは後半、各社から発売されていたマイコンキットの説明の部分だけで、前半はほとんど覚えていなかった。当時はデジタル回路を学んでいなかったので前半を理解できたとは思えない。ただワクワク感は第1作の夢のような話から実際の回路の話になったので「難しい〜。僕にはできそうもない。」と思いながら読んでいたことだろう。
もし本書を読むのであれば前もって「改訂版 電子回路の「しくみ」と「基本」 :小峯龍男」や「改訂版 デジタル回路の「しくみ」と「基本」:小峯龍男」などを読んでおくとよいだろう。
第1作の内容をさらに深く解説し、当時のコンピュータの状況が詳しく読み取れる好書である。コンピュータの原理を学ぶという意味では、現代でも入門用として使えそうな1冊だ。
「マイ・コンピュータ入門―コンピュータはあなたにもつくれる:安田寿明」(リンク2)
「マイ・コンピュータをつくる―組み立てのテクニック:安田寿明」(リンク2)
「マイコンピュータをつかう―周辺機器と活用の実際:安田寿明」



関連記事:
安田寿明先生の「マイ・コンピュータ」3部作(ブルーバックス)
http://blog.goo.ne.jp/ktonegaw/e/e54e4eb38380ff2ff2f51747ca7b4f75
マイ・コンピュータ入門―コンピュータはあなたにもつくれる:安田寿明
http://blog.goo.ne.jp/ktonegaw/e/997e2c40fda774b25ebd5561336a7bfe
NEC TK-80やワンボードマイコンのこと
http://blog.goo.ne.jp/ktonegaw/e/36db2417701c58efa1ac81343e70227b
真空管式コンピュータへのノスタルジア(EDSAC)
http://blog.goo.ne.jp/ktonegaw/e/14c9aeedfcda78c9fd9ff4b677435283
ファインマン計算機科学:ファインマン, A.ヘイ, R.アレン
http://blog.goo.ne.jp/ktonegaw/e/4f7f453019fd463ed2bfdeaa7b288d79
量子コンピュータ入門:宮野健次郎、古澤明
http://blog.goo.ne.jp/ktonegaw/e/ef75709187cf4b35a12f2d9fdf73a320
応援クリックをお願いします!このブログのランキングはこれらのサイトで確認できます。




「マイ・コンピュータをつくる―組み立てのテクニック:安田寿明」

まえがき
第1章:ひろがるマイ・コンピュータ時代
- プロローグ/マイクロ・コンピュータの成長性
- マイクロ・コンピュータの種別
- マイコンの主役は4ビット型コンピュータ
- 工場向けの4ビット型/マイ・コンピュータには8ビット以上を
- マイコン・キットの二つの目的/汎用性の8ビット型
- コンピュータ・ホビイストの誕生
第2章:マイ・コンピュータの基礎
- 高級電卓用のi4004/複雑怪奇な手づくり1号機
- i8008のターヘル・アナトミア
- 超小型誇示?のi8008/複雑怪奇なi8008の動作
- 時間分割多重化のしくみ/電極数現象でキャラメル大に
- 小さくしたため周囲は複雑化
- 第二世代マイクロ・コンピュータの誕生
- わずか大学ノート大のコンピュータ
- ワンボード・コンピュータの構成
- プリント基板とは/マイコン・キットの生い立ち
- コンピュータの三要素/インタフェース機能とは
- 「ノイマン・マシン」とは/メモリの効用
- 頭脳の秘密は記憶装置に?/メモリの種別
- 記憶の消失/どれだけ記憶できるか
- ROMとPROM
第3章:ワンボードからワンチップ・コンピュータへ
- 8080型の最小構成
- “脳波発生”のクロック・ジェネレータ
- 動作基準時間の尺度/CPUの動作状態
- システム制御と時間整合/集積回路の区分
- コンピュータかプロセッサか/たった一個でコンピュータ
- 機械のためだけのマイ・コンピュータ
- i8085コンピュータ/i8085の機能
- LSI3個で構成/プリント基板のつくり方
第4章:電子ソロバンをつくろう
- 手足のないダルマ・コンピュータ
- 2進法なんかこわくない/ソロバンは5進/10進法
- ソロバンで練習してみよう/ひとつ玉ソロバンをつくる
- 電源装置のつくり方/電子ソロバンで練習しよう
第5章:コンピュータ本体をつくる
- 事前準備は入念に/配線作業の注意点
- メモリ部の制作/事前の点検整備
- MOS・LSIの装着/メモリの動作チェック
- CPUはMC6802/マイ・コンピュータの構成
- 手づくり向きの1石コンピュータ
第6章:マイ・コンピュータのいろいろ
- 育て上げるには時間と費用が
- メーカー製の組み立てキットもある
- インテル SDK-85
- NEC TK-80
- モトローラ MEK6800II
- 日立 H68/TR
- IMSAI-8048
- ロジック・システムズ MP-80
- NS SC/MPキット
- FCI F8キット
- インターシル・サンプラー・キット
- 東芝 TLCS12A・EX-12/05
- パナファコムLKIT/16
- その他のマイコン・キット
- マイコンからハンサム・コンピュータへ
- 最初のホーム・コンピュータ ALTAIR8800
- アマチュア向けのSWTP
- 動き出した巨大資本
- ホーム・コンピュータへの旅