「
プリンストン 数学大全(朝倉書店)」
内容:
【「読める」数学レファレンス】
「数学とは何か」「数学の起源とは」から現代数学の全体像,数学と他分野との連関までをカバーする,初学者でもアクセスしやすい総合事典。
プリンストン大学出版局刊行の大著「Princeton Companion to Mathematics」の全訳。
ティモシー・ガワーズ,テレンス・タオ,マイケル・アティヤほか多数のフィールズ賞受賞者を含む一流の数学者・数学史家がやさしく読みやすいスタイルで数学の諸相を紹介する。数学愛好家から数学系学生,研究者まで幅広く活用できる一冊。
純粋数学を俯瞰するだけでなく,数学が隣接諸科学(経済学,金融,統計学,情報工学ほか)にどのような基礎を与えているかについても詳述した,「読める」数学総合事典。「ピタゴラス」「ゲーデル」など96人の数学者の評伝付き。
2015年11月刊行、1200ページ。
朝倉書店さんから「
プリンストン 数学大全」という数学大事典が発売されたので発売情報としてお知らせしておこう。(朝倉書店のホームページには11月20日発売と書かれているがAmazonではすでに購入可能になっている。)
今週末から「
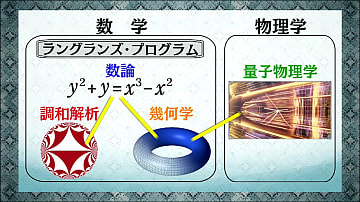
NHK数学ミステリー白熱教室」が始まるので現代数学に対する世間の関心は高まるだろう。数学事典を発売するにはちょうどよいタイミングだ。
とはいえ1200ページ(重量は2.15キログラム)あるから通読するのは難しそう。僕は書店で実物を見てから購入を検討したい。地元に大型書店がない人は実物を確認できないので、このような大著はサンプルページがホームページやオンライン書店から見れるとよいのにと思った。(朝倉書店さまから連絡があり、見本ページを掲載してくださるそうです。またTwitterでは見本ページを公開していただきました。
ここをクリックしてください。)
僕のブログでは読み終えた本について紹介記事(感想記事)を書いているが、このページ数だときついと思う。でも座右に置いていつでも調べられるようにしておきたい本であるには違いない。目次を見ると「第 III 部 数学の概念」は翻訳前の英語の順番で項目が並んでいるようだ。
本の詳細は朝倉書店のホームページで確認してほしい。
「プリンストン 数学大全」:朝倉書店のホームページ
http://www.asakura.co.jp/books/isbn/978-4-254-11143-9/
ご購入はこちらからどうぞ。
「
プリンストン 数学大全(朝倉書店)」
![]()
編集部から
「数学愛好者にとっての優れた道しるべとして」
森重文先生(京都大学教授、国際数学連合総裁、1990年フィールズ賞受賞)ご推薦
「数学愛好者にとっての優れた道しるべとして、プロの数学者にとっては専門外の分野の理解に、本書は頼りになる一冊である。古今東西の数学を見渡し、多岐にわたる分野を網羅して、それぞれ選りすぐりの世界的権威が分かりやすく解説している。そのような著書が、数学を知り尽くした翻訳陣のおかげで、日本語で提供されることになった。本書を拠り所として数学への親しみと理解が一層深まるに違いない。」
数学を「全体として」引き受ける
森田真生先生(独立研究者)ご推薦
「数学世界の全景を一望してみたい。数学を志したことのある人ならば、誰もが一度は心に抱く願いだろう。本書はそんな無謀な願いを、形にしたような本である。数学のすべてが描かれているわけでは無論ないが、遠近様々な視点から編まれた数学の一大パノラマだ。専門分化が著しい現代において、自分なりの数学の「眺望」を得ることは容易ではない。それでも数学を「全体として」引き受けようという稀有な情熱がこの本を貫いている。溢れる数学的思考の流れに身をまかせるように、好きな場所からページを繰ってみてほしい。「数学をもっと勉強したい」と心に火がつくこと請け合いである。」
翻訳の元になった原書はこちら。原書は重量2.7キログラムもあるそうなのでKindle版をiPadに入れて読めるのがうれしい。
「
The Princeton Companion to Mathematics」(
Kindle版)
![]()
応援クリックをお願いします!
![にほんブログ村 科学ブログ 物理学へ]()
![人気ブログランキングへ]()
![]()
![]()
![]()
![]()
![]()
「
プリンストン 数学大全(朝倉書店)」
![]()
目次
第 I 部 イントロダクション
I.1 数学とは何か?
I.2 数学における言語と文法
I.3 いくつかの基本的な数学的定義
I.4 数学研究の一般的目標
第 II 部 現代数学の起源
II.1 数から数体系へ
II.2 幾何学
II.3 抽象代数学の発展
II.4 アルゴリズム
II.5 解析学における厳密さの発展
II.6 証明の考え方の発展
II.7 数学の基礎における危機
第 III 部 数学の概念
III.1 選択公理
III.2 決定性公理
III.3 ベイズ解析
III.4 組ひも群
III.5 ビルディング
III.6 カラビ-ヤウ多様体
III.7 基数
III.8 圏
III.9 コンパクト性とコンパクト化
III.10 計算量クラス
III.11 可算および非可算集合
III.12 C*環
III.13 曲率
III.14 デザイン
III.15 行列式
III.16 微分形式と積分
III.17 次元
III.18 超関数
III.19 双対性
III.20 力学系とカオス
III.21 楕円曲線
III.22 ユークリッド互除法と連分数
III.23 オイラー方程式とナヴィエ-ストークス方程
III.24 エクスパンダー
III.25 指数関数と対数関数
III.26 高速フーリエ変換
III.27 フーリエ変換
III.28 フックス群
III.29 関数空間
III.30 ガロア群
III.31 ガンマ関数
III.32 母関数
III.33 種数
III.34 グラフ
III.35 ハミルトニアン
III.36 熱方程式
III.37 ヒルベルト空間
III.38 ホモロジーとコホモロジー
III.39 ホモトピー群
III.40 イデアル類群
III.41 無理数超越数
III.42 イジングモデル
III.43 ジョルダン標準形
III.44 結び目多項式
III.45 K理論
III.46 リーチ格子
III.47 L関数
III.48 リー理論
III.49 線形および非線形波動とソリトン
III.50 線形作用素とその性質
III.51 数論における局所と大域
III.52 マンデルブロ集合
III.53 多様体
III.54 マトロイド
III.55 測度
III.56 距離空間
III.57 集合論のモデル
III.58 合同式の算法
III.59 モジュラー形式
III.60 モジュライ空間
III.61 モンスター群
III.62 ノルム空間とバナッハ空間
III.63 数体
III.64 最適化とラグランジュ未定乗数法
III.65 軌道体
III.66 順序数
III.67 ペアノの公理系
III.68 置換群
III.69 相転移
III.70 π
III.71 確率分布
III.72 射影空間
III.73 2次形式
III.74 量子計算
III.75 量子群
III.76 四元数,八元数,ノルム斜体
III.77 表現
III.78 リッチ流
III.79 リーマン面
III.80 リーマンのゼータ関数
III.81 環,イデアル,加群
III.82 概型(スキーム)
III.83 シュレーディンガー方程式
III.84 シンプレクス法
III.85 特殊関数
III.86 スペクトル
III.87 球面調和関数
III.88 シンプレクティック多様体
III.89 テンソル積
III.90 位相空間
III.91 変換
III.92 三角関数
III.93 普遍被覆空間
III.94 変分法
III.95 代数多様体
III.96 ベクトル束
III.97 フォンノイマン環
III.98 ウェーブレット
III.99 ツェルメロ-フレンケルの公理系
第 IV 部 数学の諸分野
IV.1 代数的数
IV.2 解析的整数論
IV.3 計算数論
IV.4 代数幾何学
IV.5 数論幾何学
IV.6 代数的位相幾何学
IV.7 微分位相幾何学
IV.8 モジュライ空間
IV.9 表現論
IV.10 幾何学的組合せ群論
IV.11 調和解析
IV.12 偏微分方程式
IV.13 一般相対論とアインシュタイン方程式
IV.14 力学系理論
IV.15 作用素環
IV.16 ミラー対称性
IV.17 頂点作用素代数
IV.18 数え上げ組合せ論と代数的組合せ論
IV.19 極値的および確率的な組合せ論
IV.20 計算複雑さ
IV.21 数値解析
IV.22 集合論
IV.23 ロジックとモデル理論
IV.24 確率過程
IV.25 臨界現象の確率モデル
IV.26 高次元幾何と確率論的アナロジー
第 V 部 定理と問題
V.1 ABC予想
V.2 アティヤ-シンガーの指数定理
V.3 バナッハ-タルスキの逆理
V.4 バーチ-スウィナートン=ダイヤー予想
V.5 カールソンの定理
V.6 中心極限定理
V.7 有限単純群の分類
V.8 ディリクレの定理
V.9 エルゴード定理
V.10 フェルマーの最終定理
V.11 不動点定理
V.12 4色定理
V.13 代数学の基本定理
V.14 算術の基本定理
V.15 ゲーデルの定理
V.16 グロモフの多項式増大度定理
V.17 ヒルベルトの零点定理
V.18 連続体仮説の独立性
V.19 不等式
V.20 停止問題の非可解性
V.21 5 次方程式の非可解性
V.22 リューヴィルの定理とロスの定理
V.23 モストフの強剛性定理
V.24 P対NP問題
V.25 ポアンカレ予想
V.26 素数定理とリーマン予想
V.27 加法的整数論における問題と結果
V.28 平方剰余の相互法則から類体論へ
V.29 曲線上の有理点とモーデル予想
V.30 特異点解消
V.31 リーマン-ロッホの定理
V.32 ロバートソン-セイモアの定理
V.33 3体問題
V.34 一意化定理
V.35 ヴェイユ予想
第 VI 部 数学者
VI.1 ピタゴラス(前569頃-前494頃)
VI.2 ユークリッド(前325頃-前265頃)
VI.3 アルキメデス(前287頃-前212頃)
VI.4 アポロニウス(前262頃-前190頃)
VI.5 アル・フワーリズミー(800-847)
VI.6 ピサのレオナルド(フィボナッチ)(1170頃-1250頃)
VI.7 ジロラモ・カルダーノ(1501-1576)
VI.8 ラファエル・ボンベッリ(1526-1572以降)
VI.9 フランソワ・ヴィエート(1540-1603)
VI.10 シモン・ステヴィン(1548-1620)
VI.11 ルネ・デカルト(1596-1650)
VI.12 ピエール・フェルマー(160?-1665)
VI.13 ブレーズ・パスカル(1623-1662)
VI.14 アイザック・ニュートン(1642-1727)
VI.15 ゴットフリート・ヴィルヘルム・ライプニッツ(1646-1716)
VI.16 ブルック・テイラー(1685-1731)
VI.17 クリスティアン・ゴールドバッハ(1690-1764)
VI.18 ベルヌーイ家の人々(18世紀頃)
VI.19 レオンハルト・オイラー(1707-1783)
VI.20 ジャン・ル・ロン・ダランベール(1717-1783)
VI.21 エドワード・ウェアリング(1735頃-1798)
VI.22 ジョゼフ・ルイ・ラグランジュ(1736-1813)
VI.23 ピエール=シモン・ラプラス(1749-1827)
VI.24 アドリアン=マリー・ルジャンドル(1752-1833)
VI.25 ジャン・バプティスト・ジョゼフ・フーリエ(1768-1830)
VI.26 カール・フリードリヒ・ガウス(1777-1855)
VI.27 シメオン=ドニ・ポアソン(1781-1840)
VI.28 ベルナルト・ボルツァーノ(1781-1848)
VI.29 オギュスタン=ルイ・コーシー(1789-1857)
VI.30 アウグスト・フェルディナント・メビウス(1790-1868)
VI.31 ニコライ・イワノヴィッチ・ロバチェフスキー(1792-1856)
VI.32 ジョージ・グリーン(1793-1841)
VI.33 ニールス・ヘンリク・アーベル(1802-1829)
VI.34 ヤーノシュ・ボヤイ(1802-1860)
VI.35 カール・グスタフ・ヤコブ・ヤコビ(1804-1851)
VI.36 ペーター・グスタフ・ルジューヌ・ディリクレ(1805-1859)
VI.37 ウィリアム・ローワン・ハミルトン(1805-1865)
VI.38 オーガスタス・ド・モルガン(1806-1871)
VI.39 ジョゼフ・リューヴィル(1809-1882)
VI.40 エドゥアルト・クンマー(1810-1893)
VI.41 エヴァリスト・ガロア(1811-1832)
VI.42 ジェームズ・ジョゼフ・シルヴェスター(1814-1897)
VI.43 ジョージ・ブール(1815-1864)
VI.44 カール・ワイエルシュトラス(1815-1897)
VI.45 パフヌティ・チェビシェフ(1821-1894)
VI.46 アーサー・ケイリー(1821-1895)
VI.47 シャルル・エルミート(1822-1901)
VI.48 レオポルト・クロネッカー(1823-1891)
VI.49 ゲオルク・フリードリヒ・ベルンハルト・リーマン(1826-1866)
VI.50 ユリウス・ヴィルヘルム・リヒャルト・デデキント(1831-1916)
VI.51 エミール・レオナール・マシュー(1835-1890)
VI.52 カミーユ・ジョルダン(1838-1922)
VI.53 ソフス・リー(1842-1899)
VI.54 ゲオルク・カントール(1845-1918)
VI.55 ウィリアム・キングダム・クリフォード(1845-1879)
VI.56 ゴットロープ・フレーゲ(1848-1925)
VI.57 クリスティアン・フェリックス・クライン(1849-1925)
VI.58 フェルディナント・ゲオルク・フロベニウス(1849-1917)
VI.59 ソーニャ・コワレフスカヤ(1850-1891)
VI.60 ウィリアム・バーンサイド(1852-1927)
VI.61 ジュール=アンリ・ポアンカレ(1854-1912)
VI.62 ジュゼッペ・ペアノ(1858-1932)
VI.63 ダーフィト・ヒルベルト(1858-1943)
VI.64 ヘルマン・ミンコフスキー(1864-1909)
VI.65 ジャック・アダマール(1865-1963)
VI.66 イヴァール・フレドホルム(1866-1927)
VI.67 シャルル=ジャン・ド・ラ・ヴァレ・プーサン(1866-1962)
VI.68 フェリックス・ハウスドルフ(1868-1942)
VI.69 エリー・ジョゼフ・カルタン(1869-1951)
VI.70 エミール・ボレル(1871-1956)
VI.71 バートランド・ラッセル(1872-1970)
VI.72 アンリ・ルベーグ(1875-1941)
VI.73 ゴッドフリー・ハロルド・ハーディ(1877-1947)
VI.74 フレデリック・リース(1880-1956)
VI.75 ライツェン・エヒベルトゥス・ヤン・ブラウアー(1881-1966)
VI.76 エミー・ネーター(1882-1935)
VI.77 ヴァツワフ・シェルピンスキ(1882-1969)
VI.78 ジョージ・バーコフ(1884-1944)
VI.79 ジョン・エデンサー・リトルウッド(1885-1977)
VI.80 ヘルマン・ワイル(1885-1955)
VI.81 トアルフ・スコーレム(1887-1963)
VI.82 シュリニヴァーサ・ラマヌジャン(1887-1920)
VI.83 リヒャルト・クーラント(1888-1972)
VI.84 ステファン・バナッハ(1892-1945)
VI.85 ノーバート・ウィーナー(1894-1964)
VI.86 エミール・アルティン(1898-1962)
VI.87 アルフレト・タルスキ(1901-1983)
VI.88 アンドレイ・ニコライヴィッチ・コルモゴロフ(1903-1987)
VI.89 アロンゾ・チャーチ(1903-1995)
VI.90 ウィリアム・ヴァランス・ダグラス・ホッジ(1903-1975)
VI.91 ジョン・フォン・ノイマン(1903-1957)
VI.92 クルト・ゲーデル(1906-1978)
VI.93 アンドレ・ヴェイユ(1906-1998)
VI.94 アラン・チューリング(1912-1954)
VI.95 アブラハム・ロビンソン(1918-1974)
VI.96 ニコラ・ブルバキ(1935-)
第 VII 部 数学の影響
VII.1 数学と化学
VII.2 数理生物学
VII.3 ウェーブレットとその応用
VII.4 ネットワークにおける交通の数学
VII.5 アルゴリズム設計の数理
VII.6 情報伝達の信頼性
VII.7 数学と暗号学
VII.8 数学と経済学的推論
VII.9 金融数学
VII.10 数理統計学
VII.11 数学と医学統計
VII.12 解析学と分析哲学
VII.13 数学と音楽
VII.14 数学と美術
第 VIII 部 展望
VIII.1 問題を解くこつ
VIII.2 「なぜ数学をするのか?」と問われたら
VIII.3 数学の普遍性
VIII.4 ニューメラシー
VIII.5 経験科学としての数学
VIII.6 若き数学者への助言
VIII.7 数学年表
索引