3次元の球
球と球面
この連載記事では多次元空間のお話をさせていただいているのですから、多次元の球と球面の話をしないわけにはいきません。この記事では前回の記事の最後でお約束したように、第7回や前回の記事で確認した「4次元空間に2次元物体を置くと一般的に3次元空間からは1次元の曲線として観測される。」が正しいことを、球と球面の話を使って説明させていただきます。
ところで大栗博司先生がお書きになった「重力とは何か」の第3章「重力はなぜ生じるか - 一般相対論の世界」のはじめのほうに「4次元の球体が私たちの世界を訪れたときの様子について書かれています。この本では「私たちには見ることのできない方向から突如として空間に「点」が現れ、それが徐々に広がって「球」になる。」と説明しています。今回の記事はその部分がよくわからなかった方にもお役に立つはずです。
3次元の球と2次元の球面
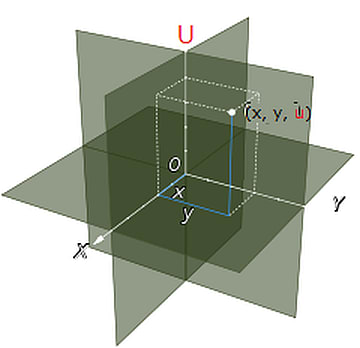
記事トップの画像は「3次元の球」です。見ることはできませんが中身も詰まっています。数学でこのような球を定義するときは、次のように表現します。
3次元空間の1点(たとえば座標の原点)からの距離が一定値以下にある点の集合
座標の原点は球の中心です。
そして球の表面は「球面」ですよね?3次元球の表面は「面」ですから2次元の曲面です。球の中身を空っぽにしたもので、次の画像の赤い曲面を8つ張り合わせた形になります。
![]()
この球面は数学では「2次元の球面」と呼び、次のように定義されます。
3次元空間の1点(たとえば座標の原点)からの距離が一定値にある点の集合
2次元の球面は3次元の球の外部との「境界」になっていますね。
2次元の球と1次元の球面
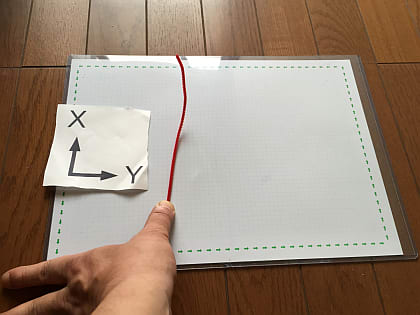
ひとつ次元を下げて2次元(平面)の世界で考えてみましょう。
次の画像は「円」ですが、「丸」とか「真ん丸」などいろいろな名前で呼ばれています。けれどもこれは3次元の球の次元を1つ下げたものですから「2次元の球」と呼ぶことにしましょう。
![]()
すると2次元の球の定義は次のようになります。
2次元空間の1点(たとえば座標の原点)からの距離が一定値以下にある点の集合
座標の原点は円の中心です。
2次元の球(すなわち円)の外周のことも「円」や「丸」と呼んでいますが、正しくは「円周」と呼びます。このような形です。
![]()
円周は1次元の曲線です。これは「2次元の球面」の外周(外との境界部分)のことですから「1次元の球面」と呼ぶことにしましょう。定義は次のようになります。
2次元空間の1点(たとえば座標の原点)からの距離が一定値にある点の集合
ここまでの説明で次の物体が登場しました。
3次元の球と、その境界としての2次元の球面
2次元の球と、その境界としての1次元の球面
さて、さらに次元を下げて1次元の空間には球や球面はあるのでしょうか?もちろんあります。2次元の球や1次元の球面の定義で次元を1つ下げればよいだけです。
1次元の球と0次元の球面
2次元の球の定義の次元をひとつ下げれば、次のようになりますね。これが「1次元の球」の定義です。
1次元空間の1点(たとえば座標の原点)からの距離が一定値以下にある点の集合
画像であらわすと、このようになります。つまり線分のことなのです。線分は1次元ですしね。奇妙に思えるかもしれませんが、これが定義から導かれる自然な形です。
![]()
座標の原点は線分の中点です。
同じようにして「0次元の球面」の定義はこうなります。
1次元空間の1点(たとえば座標の原点)からの距離が一定値にある点の集合
形はこうなります。座標の原点から等しい距離にある2つの点のことです。
![]()
N次元の球と(N-1)次元の球面
同じように考えて、球や球面の定義を4次元以上に拡張することもできます。残念ながらこのような球や球面を画像で示すことはできません。
4次元の球の定義:
4次元空間の1点(たとえば座標の原点)からの距離が一定値以下にある点の集合
3次元の球面の定義:
4次元空間の1点(たとえば座標の原点)からの距離が一定値にある点の集合
続けると球と球面はいくらでも高次元化できますね。
5次元の球と、その境界としての4次元の球面
6次元の球と、その境界としての5次元の球面
7次元の球と、その境界としての6次元の球面
8次元の球と、その境界としての7次元の球面
N次元の球と、その境界としての(N-1)次元の球面
ちなみに「ポアンカレ予想」は4次元の球の境界である「3次元の球面」についての話、「エキゾチックな球面」は8次元の球の境界である「7次元の球面」についての話です。どちらも私たちの3次元世界には存在できない高い次元の空間や物体の性質を述べているわけです。
~次元の球や~次元の球面という呼び方と、日常用語との対応がこんがらかってしまった方がいるかもしれませんので、表にまとめておきました。
![]()
次に球や球面を切断することを考えてみましょう。
2次元の球や1次元の球面の切断
2次元の球を直線で切ってみましょう。これは2次元空間にある2次元の球の話です。このようになりますね。
![]()
2次元の球を切ると青い線分があらわれます。これは「1次元の球」とも言えますよね?つまり「2次元の球を切断すると1次元の球が現れる。」と言えるのではないでしょうか?
1次元の球面も直線で切ってみます。このように2つの青い点が現れます。
![]()
2つの青い点は「0次元の球面」のことですから「1次元の球面を切断すると0次元の球面が現れる。」と言えそうです。
3次元の球や2次元の球面の切断
3次元の球を平面で切ってみましょう。これは3次元空間にある3次元の球の話です。このようになりますね。
![]()
現れたのは円ですから「2次元の球」と言えます。つまり「3次元の球を切断すると2次元の球が現れる。」と言えます。
2次元の球面も切ってみましょう。このようになります。この球の中は空っぽです。
![]()
現れたのは円周ですから「1次元の球面」です。これは「2次元の球面を切断すると1次元の球面が現れる。」ということです。
整理すると、次の2つのことが言えます。
2≦Nとするとき、N次元空間で:
- N次元の球を(N-1)次元の物体を使って切断すると(N-1)次元の球があらわれる。
- (N-1)次元の球面を(N-1)次元の物体を使って切断すると(N-2)次元の球面があらわれる。
表にしてみました。
![]()
また、この表から次のことが言えることがおわかりでしょうか?
- 4次元空間で4次元球を3次元物体(空間)で切断すると3次元の球が現れる。
これと大栗先生が「重力とは何か」の中で「4次元球が私たちの世界を訪れるとき、私たちには見ることのできない方向から突如として空間に「点」が現れ、それが徐々に広がって「球」になる。」が対応しているわけです。
表では黄色いセルの箇所で球の次元が3であることからそのように言えるのです。
![]()
それでは「4次元空間に2次元物体を置くと一般的に3次元空間からは1次元の曲線として観測される。」が正しいことは、この表からどのようにしてわかるのでしょうか?
いいえ、この表からはわかりません。この表は4次元空間に4次元球を置いた場合です。今回は2次元の曲面を置いた場合を知りたいわけですから、4次元空間に置くのは3次元球のはずです。
つまり、次元の数字をひとつずつ減らして、次の表を完成させます。さきほどの表と比べてみてください。
![]()
この表によると4次元空間に置いた2次元曲面(表の黄緑色のセル)を3次元空間で切断して見ると、1次元の曲線(黄色いセル)として見えることがわかります。
さて、次回の記事ですが3次元空間での話をする予定です。第5回までの記事では「ひもが絡まるのは3次元空間だけ」という話をしましたが、「ひもはなぜ絡まりやすいのか」については、まだ説明していません。次回はこれを説明いたします。
応援クリックをお願いします!
![にほんブログ村 科学ブログ 物理学へ]()
![人気ブログランキングへ]()
![]()
![]()
![]()
![]()
![]()
球と球面
この連載記事では多次元空間のお話をさせていただいているのですから、多次元の球と球面の話をしないわけにはいきません。この記事では前回の記事の最後でお約束したように、第7回や前回の記事で確認した「4次元空間に2次元物体を置くと一般的に3次元空間からは1次元の曲線として観測される。」が正しいことを、球と球面の話を使って説明させていただきます。
ところで大栗博司先生がお書きになった「重力とは何か」の第3章「重力はなぜ生じるか - 一般相対論の世界」のはじめのほうに「4次元の球体が私たちの世界を訪れたときの様子について書かれています。この本では「私たちには見ることのできない方向から突如として空間に「点」が現れ、それが徐々に広がって「球」になる。」と説明しています。今回の記事はその部分がよくわからなかった方にもお役に立つはずです。
3次元の球と2次元の球面
記事トップの画像は「3次元の球」です。見ることはできませんが中身も詰まっています。数学でこのような球を定義するときは、次のように表現します。
3次元空間の1点(たとえば座標の原点)からの距離が一定値以下にある点の集合
座標の原点は球の中心です。
そして球の表面は「球面」ですよね?3次元球の表面は「面」ですから2次元の曲面です。球の中身を空っぽにしたもので、次の画像の赤い曲面を8つ張り合わせた形になります。

この球面は数学では「2次元の球面」と呼び、次のように定義されます。
3次元空間の1点(たとえば座標の原点)からの距離が一定値にある点の集合
2次元の球面は3次元の球の外部との「境界」になっていますね。
2次元の球と1次元の球面
ひとつ次元を下げて2次元(平面)の世界で考えてみましょう。
次の画像は「円」ですが、「丸」とか「真ん丸」などいろいろな名前で呼ばれています。けれどもこれは3次元の球の次元を1つ下げたものですから「2次元の球」と呼ぶことにしましょう。

すると2次元の球の定義は次のようになります。
2次元空間の1点(たとえば座標の原点)からの距離が一定値以下にある点の集合
座標の原点は円の中心です。
2次元の球(すなわち円)の外周のことも「円」や「丸」と呼んでいますが、正しくは「円周」と呼びます。このような形です。

円周は1次元の曲線です。これは「2次元の球面」の外周(外との境界部分)のことですから「1次元の球面」と呼ぶことにしましょう。定義は次のようになります。
2次元空間の1点(たとえば座標の原点)からの距離が一定値にある点の集合
ここまでの説明で次の物体が登場しました。
3次元の球と、その境界としての2次元の球面
2次元の球と、その境界としての1次元の球面
さて、さらに次元を下げて1次元の空間には球や球面はあるのでしょうか?もちろんあります。2次元の球や1次元の球面の定義で次元を1つ下げればよいだけです。
1次元の球と0次元の球面
2次元の球の定義の次元をひとつ下げれば、次のようになりますね。これが「1次元の球」の定義です。
1次元空間の1点(たとえば座標の原点)からの距離が一定値以下にある点の集合
画像であらわすと、このようになります。つまり線分のことなのです。線分は1次元ですしね。奇妙に思えるかもしれませんが、これが定義から導かれる自然な形です。

座標の原点は線分の中点です。
同じようにして「0次元の球面」の定義はこうなります。
1次元空間の1点(たとえば座標の原点)からの距離が一定値にある点の集合
形はこうなります。座標の原点から等しい距離にある2つの点のことです。

N次元の球と(N-1)次元の球面
同じように考えて、球や球面の定義を4次元以上に拡張することもできます。残念ながらこのような球や球面を画像で示すことはできません。
4次元の球の定義:
4次元空間の1点(たとえば座標の原点)からの距離が一定値以下にある点の集合
3次元の球面の定義:
4次元空間の1点(たとえば座標の原点)からの距離が一定値にある点の集合
続けると球と球面はいくらでも高次元化できますね。
5次元の球と、その境界としての4次元の球面
6次元の球と、その境界としての5次元の球面
7次元の球と、その境界としての6次元の球面
8次元の球と、その境界としての7次元の球面
N次元の球と、その境界としての(N-1)次元の球面
ちなみに「ポアンカレ予想」は4次元の球の境界である「3次元の球面」についての話、「エキゾチックな球面」は8次元の球の境界である「7次元の球面」についての話です。どちらも私たちの3次元世界には存在できない高い次元の空間や物体の性質を述べているわけです。
~次元の球や~次元の球面という呼び方と、日常用語との対応がこんがらかってしまった方がいるかもしれませんので、表にまとめておきました。

次に球や球面を切断することを考えてみましょう。
2次元の球や1次元の球面の切断
2次元の球を直線で切ってみましょう。これは2次元空間にある2次元の球の話です。このようになりますね。

2次元の球を切ると青い線分があらわれます。これは「1次元の球」とも言えますよね?つまり「2次元の球を切断すると1次元の球が現れる。」と言えるのではないでしょうか?
1次元の球面も直線で切ってみます。このように2つの青い点が現れます。

2つの青い点は「0次元の球面」のことですから「1次元の球面を切断すると0次元の球面が現れる。」と言えそうです。
3次元の球や2次元の球面の切断
3次元の球を平面で切ってみましょう。これは3次元空間にある3次元の球の話です。このようになりますね。

現れたのは円ですから「2次元の球」と言えます。つまり「3次元の球を切断すると2次元の球が現れる。」と言えます。
2次元の球面も切ってみましょう。このようになります。この球の中は空っぽです。

現れたのは円周ですから「1次元の球面」です。これは「2次元の球面を切断すると1次元の球面が現れる。」ということです。
整理すると、次の2つのことが言えます。
2≦Nとするとき、N次元空間で:
- N次元の球を(N-1)次元の物体を使って切断すると(N-1)次元の球があらわれる。
- (N-1)次元の球面を(N-1)次元の物体を使って切断すると(N-2)次元の球面があらわれる。
表にしてみました。

また、この表から次のことが言えることがおわかりでしょうか?
- 4次元空間で4次元球を3次元物体(空間)で切断すると3次元の球が現れる。
これと大栗先生が「重力とは何か」の中で「4次元球が私たちの世界を訪れるとき、私たちには見ることのできない方向から突如として空間に「点」が現れ、それが徐々に広がって「球」になる。」が対応しているわけです。
表では黄色いセルの箇所で球の次元が3であることからそのように言えるのです。

それでは「4次元空間に2次元物体を置くと一般的に3次元空間からは1次元の曲線として観測される。」が正しいことは、この表からどのようにしてわかるのでしょうか?
いいえ、この表からはわかりません。この表は4次元空間に4次元球を置いた場合です。今回は2次元の曲面を置いた場合を知りたいわけですから、4次元空間に置くのは3次元球のはずです。
つまり、次元の数字をひとつずつ減らして、次の表を完成させます。さきほどの表と比べてみてください。

この表によると4次元空間に置いた2次元曲面(表の黄緑色のセル)を3次元空間で切断して見ると、1次元の曲線(黄色いセル)として見えることがわかります。
さて、次回の記事ですが3次元空間での話をする予定です。第5回までの記事では「ひもが絡まるのは3次元空間だけ」という話をしましたが、「ひもはなぜ絡まりやすいのか」については、まだ説明していません。次回はこれを説明いたします。
応援クリックをお願いします!