「宇宙と宇宙をつなぐ数学 IUT理論の衝撃： 加藤文元」（Kindle版）
内容紹介：
人類に残された最後の超難問、ABC予想に挑む!
人類に残された超難問、ABC予想の解決をも含むとするIUT(宇宙際タイヒミュラー)理論。
京都大学の望月新一教授によって構築された論文は、「未来から来た論文」と称されるなど、数学界のみならず、世界に衝撃をもたらした。
この論文は、世界で理解できるのは多く見積もっても数人、といわれるほどの難解さであり、論文の発表から6年以上たった現在もなおアクセプトに至っていないが、望月教授と、議論と親交を重ねてきた著者は、IUT理論は数学者ではない一般の人たちにもわかってもらえるような自然な考え方に根ざしていると考える。本書では、理論のエッセンスを一般の読者に向けてわかりやすく紹介。その斬新さと独創性を体感できる。理論の提者である望月新一教授の特別寄稿も収録!
2019年4月25日刊行、304ページ。
著者について：
加藤 文元: HP: http://www.math.titech.ac.jp/~bungen/index-j.html
1968年、宮城県生まれ。東京工業大学理学院数学系教授。97年、京都大学大学院理学研究科数学数理解析専攻博士後期課程修了。九州大学大学院助手、京都大学大学院准教授などを経て、2016年より現職。著書『ガロア 天才数学者の生涯』『物語 数学の歴史 正しさへの挑戦』『数学する精神 正しさの創造、美しさの発見』(以上、中公新書)『数学の想像力 正しさの深層に何があるのか』(筑摩選書)、『天に向かって続く数』(共著日本評論社)など。
加藤先生の著書： 書籍版 Kindle版
理数系書籍のレビュー記事は本書で408冊目。平成最後の紹介記事だ。
今年は「官房長官 新元号は「宇宙」と発表」というエイプリルフール記事を投稿していた。
「宇宙」という言葉は使い方や文脈によっては、「うさん臭さ」や「トンデモ」な印象を与えてしまうことがある。
提唱者の望月新一先生のホームページ（URL）内にある「IUT(宇宙際タイヒミュラー)理論」のページがあることは、数年前に気が付いていた。
宇宙際タイヒミューラー理論の拡がり
http://www.kurims.kyoto-u.ac.jp/~motizuki/project-2020-japanese.html
Image may be NSFW.
Clik here to view.
京大の先生がお書きになったページであるにも関わらず、僕は「うさん臭い」と誤解して詳しく読んでいなかったのだ。ページトップで切り替わる画像を見る限り、自分が理解できるシロモノではないことがすぐわかる。そして「日本人がABC予想を証明した」というニュースは知っていたものの、その日本人が望月先生だということに気が付いていなかったのだ。相変わらずの迂闊者である。
今回紹介する「宇宙と宇宙をつなぐ数学 IUT理論の衝撃： 加藤文元」（Kindle版）を知り、やっとIUT理論の価値に気が付かされた。
著者の加藤先生がお書きになった本は、これまで2冊紹介させていただいてとても好感を持っている。加藤先生がお書きになったのだから面白いに決まっている。案の定、本書は発売開始前からツイッター上で話題になっていて、発売開始まもなくアマゾンでは一般向け数学書の販売ランキング１位という好評ぶりだ。
加藤先生は望月先生の友人であり、2005年から2011年にかけて京大にあった加藤先生の研究室で、望月先生の新理論について議論していらっしゃったそうだ。IUT理論の誕生と成長過程を間近で見ていらっしゃったのが加藤先生なのだ。
本書は2017年に開催された「数学の祭典 MATH POWER 2017」というイベントの一部として加藤先生が行なったABC予想や宇宙際タイヒミュラー（IUT）理論の基本についての1時間25分の講演「ABC予想と新しい数学」に肉付けして書籍化したものだ。この講演動画と同じものは、その後英語字幕が付けられて、YouTubeからも見ることができる。
Inter-universal Teichmüller theory via Fumiharu Kato w/English subtitles [PROPER]
未来からきた論文、異世界の論文と呼ばれ、世界で理解している数学者はたった数名という超難解な理論であるにもかかわらず、動画をご覧になっていただくとわかるように、中学生でも理解できそうな講演だ。
数学という体系全体を私たちはひとつのものと見なしている。その世界は大まかに「数論（代数学）」、「幾何学」、「調和解析（解析学）」という３つの島に分かれ、それらの間にミステリアスなつながりがあることが、2015年に放送された「NHK数学ミステリー白熱教室」というテレビ番組や「数学の大統一に挑む：エドワード・フレンケル」という本で紹介された。
数学者の仕事は定理や予想を証明することである。それはジグソーパズルを解くように、ピースをひとつひとつ組み合わせて全体を完成させていく作業にたとえることができる。このように数学とは人類が数を数え始めて以来、数万年に渡って築き上げてきた「１つの巨大な体系」である。
難問の「ABC予想」を証明するためにも、既存の数学体系が使えるのかもしれない。しかし、望月先生はまったく違う考え方をした。これまでの数学体系は「たし算」と「かけ算」がとても複雑に絡み合っているため、ABC予想の証明を阻んでいるのだとお考えになった。証明するためにはまた別の数学体系が必要だというのだ。IUT理論や本書のタイトルで使われている「宇宙」がひとつの数学体系を意味し、本書ではこの宇宙を「数学一式」や「数学の舞台」と言い換えられている。
そして「国際」という言葉が「国と国の間の関係」を意味しているのと同じような意味で、複数の数学の舞台どうしの関係を「宇宙際（うちゅうさい）」と呼ぶことにしたわけだ。そして複素数の世界での「タイヒミュラー理論」を数論幾何学に適用したのが「IUT(宇宙際タイヒミュラー)理論」である。この新理論を応用することで、望月先生はABC予想を証明されたという。
2012年にその証明が発表されたわけだが、現在も査読中で世界中の数学者に受け入れられるまでには至っていない。その理由は主に次の３つである。
- これまでの数学ではない、新しく望月先生が創造した数学理論、数学手法が多用されているため、他の数学者ははじめから学びなおさなければならないから。
- 論文自体が難解なうえ、500ページにもおよぶから。
- この論文を理解する上で前提となる数学を理解している数学者の数が限られているから。
これまでの流れを要約すると、次のようになる。
2012年8月 IUT理論でABC予想が証明されたという論文が発表され、世界的ニュースになった。
2013年12月 論文を理解した研究者が2名あらわれた。
山下剛(京大講師)、モハメッド・サイディ(英エクセター大教授)
2014年12月 論文を理解した研究者が3名になった。
- 星裕一郎(京大講師)
- 星先生は論文の検証は数学的には終了したので、今後は理解者育成に移ると発表。検証終了宣言は2010年代後半を想定していると発言。
- 星先生によるIUT理論へ入門するための日本語の試料（PDFファイル）
http://www.kurims.kyoto-u.ac.jp/~yuichiro/intro_iut.pdf
2015年12月 英国で論文の研究集会が開催された。
- フェルマーの最終定理を解いたアンドリューワイルズや師匠のゲルトファルティングス他多数の著名な研究者含む約60名参加。
- 結果：準備論文の理解に重要な進展があったが、本体論文の検証は思うように進まなかった。
2016年7月 京大で論文の研究集会が開催。
- 主催者によると、理解者が10名以上になった。
- キランケドラヤ、ジェフリーラガリアスらが肯定的に検証継続を表明した。若手が独自の勉強会を開き、望月新一氏のもとに集い始めるなど普及が本格化している。
このように難解な数学理論を、一般人にもわかるように説明するというのが、本書のすごいところ。対象読者も中学生以上だ。
章立ては次のとおり。
第1章 IUTショック
第2章 数学者の仕事
第3章 宇宙際幾何学者
第4章 たし算とかけ算
第5章 パズルのピース
第6章 対称性通信
第7章 「行為」の計算
第8章 伝達・復元・ひずみ
第1章の「IUTショック」から僕は衝撃を受けた。難問として知られる「ABC予想」を解くために、望月先生はこれまでとはまったく違う数学を創り出したという話。この章から第3章までは講演動画には含まれていない内容だ。IUT理論がどのように誕生したか、数学の論文はどのようにして書かれ、アクセプトされていくかという話、望月先生の紹介と、これまでなされてきた加藤先生との交流が書かれている。
ここまで読むとIUT理論本体の説明がされていないにもかかわらず、これがとてつもない理論だということがわかる。加藤先生が強調なさればなさるほど、読者はやきもきしてきて「早く教えてよ！」という気分が高まっていくのだ。
理論本体の解説が始まるのは、本書を読み始めて半分くらいのところから始まる第4章「たし算とかけ算」からである。既存の数学体系では、この２つが複雑にからみあっているという話、どのようにこの２つを分離すればよいかという話である。一度目に読んだときは「２つを分離する方法」が説明されていることに気が付かなかった。後で講演動画を見て、次のようなことであると理解できた。
Image may be NSFW.
Clik here to view.![]()
Image may be NSFW.
Clik here to view.![]()
異なる２つの数学世界では、何らかの関係性をもつ必要がある。実世界の物理では２つのパラレルワールドの間で物のやり取りはできないのだが、数学のパラレルワールドでも「モノ」のやり取りはできない。しかし「コト」をやり取り（通信）はできるのだ。それが「群」として取り扱われる「対称性」という性質である。本書で解説されるのは、この3つの群だ。
- 位数4の巡回群
- 4次の二面体群
- 4次の対称群
中学生にもわかってもらうようにするため、本書では群論の説明に第6章と第7章で50ページをあてている。群論を学んでいる人は読まなくてもよいかもしれない。とりあえず読んでみたが、難しい専門用語や概念を持ち出さず、日常的な事例を使ってとても上手かつ効率的な解説がされていた。群論や創始者のガロアのことを、もっと知りたくなったら、加藤先生のこの本をお読みになるとよいだろう。
「ガロア―天才数学者の生涯 (中公新書)： 加藤文元」（Kindle版）
Image may be NSFW.
Clik here to view.![]()
最終章、第8章「伝達・復元・ひずみ」が本書でいちばん難しい。異なる２つの数学世界（舞台）でパズルのピースを合わせると「ひずみ」ができるのだ。「対称性」が舞台間で伝えられるのは部分的な情報である。この章ではどのように対称性を伝えるか、伝えられた情報からどのように復元するか、そして生じたひずみをどのように計算するかが解説される。内容が難解なだけに、比喩を使って説明するのには限界がどうしてもでてくる。それにも関わらず、大ざっぱなイメージはじゅうぶんつかむことができた。
そもそもIUT理論は本書の最後で紹介されるこの動画で視覚化されているように、常人にはとても理解できるものではないのだから。
Eteinne Farcot - The Multiradial Represenation of IUT
講演動画の最後で、加藤先生は「IUT理論は他の数学の問題に対しても使うことができると思う。」とおっしゃっている。また加藤先生が主催された「数学愛好家の集い」に参加して、直接お聞きしたのだが「今回の本は中学生以上を対象にして書いたが、理系大学生向けにもっと深く説明することもできる。」ということだそうだ。今後、IUT理論を解説した本が増えていくことを期待したい。
本書は期待をはるかに超えた本だった。一般社会のみならず数学界についてもIUT理論に対して抱かれがちな「トンデモ」なイメージを払拭し、よい意味で「とんでもない理論」、「とてつもない理論」であることを広めていくために大きな役割を果たすことだろう。
なお、理論の提者である望月新一教授の特別寄稿はKindle版のページから無料サンプルとして読むことができる。
加藤先生、興奮とスリルに満ちた本をお書きくださり、ありがとうございました。
関連記事：
数学する精神―正しさの創造、美しさの発見： 加藤文元
https://blog.goo.ne.jp/ktonegaw/e/4d706bf3aeba7eb5fe876b55b8a8496c
天に向かって続く数： 加藤文元、中井保行
https://blog.goo.ne.jp/ktonegaw/e/3d059b0a114b4bd712291a7fb81269e5
感想： NHK数学ミステリー白熱教室
https://blog.goo.ne.jp/ktonegaw/e/b0d53d030bf82e8016a1071fadb16063
数学の大統一に挑む：エドワード・フレンケル
https://blog.goo.ne.jp/ktonegaw/e/43ca100e56e15427613b009af55c8f7d
応援クリックをお願いします。
Image may be NSFW.
Clik here to view.![にほんブログ村 科学ブログ 物理学へ]()
Image may be NSFW.
Clik here to view.![人気ブログランキングへ]()
Image may be NSFW.
Clik here to view.![]()
Image may be NSFW.
Clik here to view.![]()
Image may be NSFW.
Clik here to view.![]()
Image may be NSFW.
Clik here to view.![]()
Image may be NSFW.
Clik here to view.![]()
「宇宙と宇宙をつなぐ数学 IUT理論の衝撃： 加藤文元」（Kindle版）
Image may be NSFW.
Clik here to view.![]()
はじめに
刊行によせて（望月新一：IUT理論提唱者、京都大学教授）
第1章 IUTショック
- 「イエス、グーグル！」
- 国際、銀河際、宇宙際
- 未来からやってきた論文
- 数学界の反応
- 共通の言語
- コミュニケーションパラダイム
- たし算とかけ算を分離する
- 「いざない」
- 最良のコミュニケーション
- IUT語
第2章 数学者の仕事
- 数学で新しいことができるのはなぜか？
- 数学が進歩するとは、どういうことなのか？
- 数学とは異種格闘技である！
- 論文の価値はなにで決まるのか？
- 数学は体力を使う学問である
- 「興味深い」ということ
- 理論はいかにして世界へ発信されるのか？
- 数学はお金がかかる学問である
- 数学のジャーナル
- 論文がアクセプトされるとはどういうことなのか？
- 紳士のゲーム
- そもそも人はなぜ数学するのか？
- 純粋と応用
- 楕円曲線とICカード
- ありふれたサクセスストーリー
- 数学の限りない可能性
第3章 宇宙際幾何学者
- 数学の変革
- 32歳で京大教授
- 焼肉とドラマ
- ディオファントス方程式
- 実効版モーデル予想
- タイヒミュラー理論
- 遠アーベル幾何学
- ホッジ・アラケロフ理論
- 自然であること
- アナロジー
第4章 たし算とかけ算
- 素数と素因数分解
- 根基
- ABCトリプル
- 例外的ABCトリプルとABC予想
- 強いABC予想
- その波及効果
- そもそも予想とはなにか？
- 予想はなぜ可能なのか？
- 気まぐれな素因数
- たし算的側面とかけ算的側面
- 素数が現れるタイミング
- たし算とかけ算の絡み合い
第5章 パズルのピース
- IUT理論の新しさ
- 数学の舞台
- ジグソーパズル
- 学校で教わる数学
- IUTパズル
- たし算とかけ算による正則構造
- 新しい柔軟性
- 入れ子宇宙
- 異なる舞台のピースをはめる
- テータリンク
第6章 対称性通信
- 複数の舞台で考える
- 舞台間の通信はどうするのか？
- 対称性
- 回転と鏡映
- 対称性による復元
- 復元ゲーム
- 対称性通信
- ひずみ
第7章 「行為」の計算
- 右向け右！
- 行為の合成
- 「動き」を計算する
- 「閉じている」ということ
- 記号の計算
- 記号化のご利益
- 対称性の群
- アーベル、非アーベル、遠アーベル
- 文字の置き換えゲーム
- 対称群
- 抽象的な群
- 対称性は壁を越える
- ガロア理論と「復元」
第8章 伝達・復元・ひずみ
- IUT理論がやろうとしていること
- 目指す不等式
- 異なる数学んお「舞台」のパズルのピース
- 対称性通信と計算
- テータ関数
- ひずみの計測
- 局所と大域
- 精密な同期
- まとめ
おわりにかえて 川上量生（株式会社ドワンゴ顧問）
内容紹介：
人類に残された最後の超難問、ABC予想に挑む!
人類に残された超難問、ABC予想の解決をも含むとするIUT(宇宙際タイヒミュラー)理論。
京都大学の望月新一教授によって構築された論文は、「未来から来た論文」と称されるなど、数学界のみならず、世界に衝撃をもたらした。
この論文は、世界で理解できるのは多く見積もっても数人、といわれるほどの難解さであり、論文の発表から6年以上たった現在もなおアクセプトに至っていないが、望月教授と、議論と親交を重ねてきた著者は、IUT理論は数学者ではない一般の人たちにもわかってもらえるような自然な考え方に根ざしていると考える。本書では、理論のエッセンスを一般の読者に向けてわかりやすく紹介。その斬新さと独創性を体感できる。理論の提者である望月新一教授の特別寄稿も収録!
2019年4月25日刊行、304ページ。
著者について：
加藤 文元: HP: http://www.math.titech.ac.jp/~bungen/index-j.html
1968年、宮城県生まれ。東京工業大学理学院数学系教授。97年、京都大学大学院理学研究科数学数理解析専攻博士後期課程修了。九州大学大学院助手、京都大学大学院准教授などを経て、2016年より現職。著書『ガロア 天才数学者の生涯』『物語 数学の歴史 正しさへの挑戦』『数学する精神 正しさの創造、美しさの発見』(以上、中公新書)『数学の想像力 正しさの深層に何があるのか』(筑摩選書)、『天に向かって続く数』(共著日本評論社)など。
加藤先生の著書： 書籍版 Kindle版
理数系書籍のレビュー記事は本書で408冊目。平成最後の紹介記事だ。
今年は「官房長官 新元号は「宇宙」と発表」というエイプリルフール記事を投稿していた。
「宇宙」という言葉は使い方や文脈によっては、「うさん臭さ」や「トンデモ」な印象を与えてしまうことがある。
提唱者の望月新一先生のホームページ（URL）内にある「IUT(宇宙際タイヒミュラー)理論」のページがあることは、数年前に気が付いていた。
宇宙際タイヒミューラー理論の拡がり
http://www.kurims.kyoto-u.ac.jp/~motizuki/project-2020-japanese.html
Image may be NSFW.
Clik here to view.
京大の先生がお書きになったページであるにも関わらず、僕は「うさん臭い」と誤解して詳しく読んでいなかったのだ。ページトップで切り替わる画像を見る限り、自分が理解できるシロモノではないことがすぐわかる。そして「日本人がABC予想を証明した」というニュースは知っていたものの、その日本人が望月先生だということに気が付いていなかったのだ。相変わらずの迂闊者である。
今回紹介する「宇宙と宇宙をつなぐ数学 IUT理論の衝撃： 加藤文元」（Kindle版）を知り、やっとIUT理論の価値に気が付かされた。
著者の加藤先生がお書きになった本は、これまで2冊紹介させていただいてとても好感を持っている。加藤先生がお書きになったのだから面白いに決まっている。案の定、本書は発売開始前からツイッター上で話題になっていて、発売開始まもなくアマゾンでは一般向け数学書の販売ランキング１位という好評ぶりだ。
加藤先生は望月先生の友人であり、2005年から2011年にかけて京大にあった加藤先生の研究室で、望月先生の新理論について議論していらっしゃったそうだ。IUT理論の誕生と成長過程を間近で見ていらっしゃったのが加藤先生なのだ。
本書は2017年に開催された「数学の祭典 MATH POWER 2017」というイベントの一部として加藤先生が行なったABC予想や宇宙際タイヒミュラー（IUT）理論の基本についての1時間25分の講演「ABC予想と新しい数学」に肉付けして書籍化したものだ。この講演動画と同じものは、その後英語字幕が付けられて、YouTubeからも見ることができる。
Inter-universal Teichmüller theory via Fumiharu Kato w/English subtitles [PROPER]
未来からきた論文、異世界の論文と呼ばれ、世界で理解している数学者はたった数名という超難解な理論であるにもかかわらず、動画をご覧になっていただくとわかるように、中学生でも理解できそうな講演だ。
数学という体系全体を私たちはひとつのものと見なしている。その世界は大まかに「数論（代数学）」、「幾何学」、「調和解析（解析学）」という３つの島に分かれ、それらの間にミステリアスなつながりがあることが、2015年に放送された「NHK数学ミステリー白熱教室」というテレビ番組や「数学の大統一に挑む：エドワード・フレンケル」という本で紹介された。
数学者の仕事は定理や予想を証明することである。それはジグソーパズルを解くように、ピースをひとつひとつ組み合わせて全体を完成させていく作業にたとえることができる。このように数学とは人類が数を数え始めて以来、数万年に渡って築き上げてきた「１つの巨大な体系」である。
難問の「ABC予想」を証明するためにも、既存の数学体系が使えるのかもしれない。しかし、望月先生はまったく違う考え方をした。これまでの数学体系は「たし算」と「かけ算」がとても複雑に絡み合っているため、ABC予想の証明を阻んでいるのだとお考えになった。証明するためにはまた別の数学体系が必要だというのだ。IUT理論や本書のタイトルで使われている「宇宙」がひとつの数学体系を意味し、本書ではこの宇宙を「数学一式」や「数学の舞台」と言い換えられている。
そして「国際」という言葉が「国と国の間の関係」を意味しているのと同じような意味で、複数の数学の舞台どうしの関係を「宇宙際（うちゅうさい）」と呼ぶことにしたわけだ。そして複素数の世界での「タイヒミュラー理論」を数論幾何学に適用したのが「IUT(宇宙際タイヒミュラー)理論」である。この新理論を応用することで、望月先生はABC予想を証明されたという。
2012年にその証明が発表されたわけだが、現在も査読中で世界中の数学者に受け入れられるまでには至っていない。その理由は主に次の３つである。
- これまでの数学ではない、新しく望月先生が創造した数学理論、数学手法が多用されているため、他の数学者ははじめから学びなおさなければならないから。
- 論文自体が難解なうえ、500ページにもおよぶから。
- この論文を理解する上で前提となる数学を理解している数学者の数が限られているから。
これまでの流れを要約すると、次のようになる。
2012年8月 IUT理論でABC予想が証明されたという論文が発表され、世界的ニュースになった。
2013年12月 論文を理解した研究者が2名あらわれた。
山下剛(京大講師)、モハメッド・サイディ(英エクセター大教授)
2014年12月 論文を理解した研究者が3名になった。
- 星裕一郎(京大講師)
- 星先生は論文の検証は数学的には終了したので、今後は理解者育成に移ると発表。検証終了宣言は2010年代後半を想定していると発言。
- 星先生によるIUT理論へ入門するための日本語の試料（PDFファイル）
http://www.kurims.kyoto-u.ac.jp/~yuichiro/intro_iut.pdf
2015年12月 英国で論文の研究集会が開催された。
- フェルマーの最終定理を解いたアンドリューワイルズや師匠のゲルトファルティングス他多数の著名な研究者含む約60名参加。
- 結果：準備論文の理解に重要な進展があったが、本体論文の検証は思うように進まなかった。
2016年7月 京大で論文の研究集会が開催。
- 主催者によると、理解者が10名以上になった。
- キランケドラヤ、ジェフリーラガリアスらが肯定的に検証継続を表明した。若手が独自の勉強会を開き、望月新一氏のもとに集い始めるなど普及が本格化している。
このように難解な数学理論を、一般人にもわかるように説明するというのが、本書のすごいところ。対象読者も中学生以上だ。
章立ては次のとおり。
第1章 IUTショック
第2章 数学者の仕事
第3章 宇宙際幾何学者
第4章 たし算とかけ算
第5章 パズルのピース
第6章 対称性通信
第7章 「行為」の計算
第8章 伝達・復元・ひずみ
第1章の「IUTショック」から僕は衝撃を受けた。難問として知られる「ABC予想」を解くために、望月先生はこれまでとはまったく違う数学を創り出したという話。この章から第3章までは講演動画には含まれていない内容だ。IUT理論がどのように誕生したか、数学の論文はどのようにして書かれ、アクセプトされていくかという話、望月先生の紹介と、これまでなされてきた加藤先生との交流が書かれている。
ここまで読むとIUT理論本体の説明がされていないにもかかわらず、これがとてつもない理論だということがわかる。加藤先生が強調なさればなさるほど、読者はやきもきしてきて「早く教えてよ！」という気分が高まっていくのだ。
理論本体の解説が始まるのは、本書を読み始めて半分くらいのところから始まる第4章「たし算とかけ算」からである。既存の数学体系では、この２つが複雑にからみあっているという話、どのようにこの２つを分離すればよいかという話である。一度目に読んだときは「２つを分離する方法」が説明されていることに気が付かなかった。後で講演動画を見て、次のようなことであると理解できた。
Image may be NSFW.
Clik here to view.
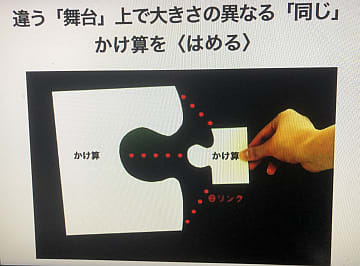
Image may be NSFW.
Clik here to view.
異なる２つの数学世界では、何らかの関係性をもつ必要がある。実世界の物理では２つのパラレルワールドの間で物のやり取りはできないのだが、数学のパラレルワールドでも「モノ」のやり取りはできない。しかし「コト」をやり取り（通信）はできるのだ。それが「群」として取り扱われる「対称性」という性質である。本書で解説されるのは、この3つの群だ。
- 位数4の巡回群
- 4次の二面体群
- 4次の対称群
中学生にもわかってもらうようにするため、本書では群論の説明に第6章と第7章で50ページをあてている。群論を学んでいる人は読まなくてもよいかもしれない。とりあえず読んでみたが、難しい専門用語や概念を持ち出さず、日常的な事例を使ってとても上手かつ効率的な解説がされていた。群論や創始者のガロアのことを、もっと知りたくなったら、加藤先生のこの本をお読みになるとよいだろう。
「ガロア―天才数学者の生涯 (中公新書)： 加藤文元」（Kindle版）
Image may be NSFW.
Clik here to view.
最終章、第8章「伝達・復元・ひずみ」が本書でいちばん難しい。異なる２つの数学世界（舞台）でパズルのピースを合わせると「ひずみ」ができるのだ。「対称性」が舞台間で伝えられるのは部分的な情報である。この章ではどのように対称性を伝えるか、伝えられた情報からどのように復元するか、そして生じたひずみをどのように計算するかが解説される。内容が難解なだけに、比喩を使って説明するのには限界がどうしてもでてくる。それにも関わらず、大ざっぱなイメージはじゅうぶんつかむことができた。
そもそもIUT理論は本書の最後で紹介されるこの動画で視覚化されているように、常人にはとても理解できるものではないのだから。
Eteinne Farcot - The Multiradial Represenation of IUT
講演動画の最後で、加藤先生は「IUT理論は他の数学の問題に対しても使うことができると思う。」とおっしゃっている。また加藤先生が主催された「数学愛好家の集い」に参加して、直接お聞きしたのだが「今回の本は中学生以上を対象にして書いたが、理系大学生向けにもっと深く説明することもできる。」ということだそうだ。今後、IUT理論を解説した本が増えていくことを期待したい。
本書は期待をはるかに超えた本だった。一般社会のみならず数学界についてもIUT理論に対して抱かれがちな「トンデモ」なイメージを払拭し、よい意味で「とんでもない理論」、「とてつもない理論」であることを広めていくために大きな役割を果たすことだろう。
なお、理論の提者である望月新一教授の特別寄稿はKindle版のページから無料サンプルとして読むことができる。
加藤先生、興奮とスリルに満ちた本をお書きくださり、ありがとうございました。
関連記事：
数学する精神―正しさの創造、美しさの発見： 加藤文元
https://blog.goo.ne.jp/ktonegaw/e/4d706bf3aeba7eb5fe876b55b8a8496c
天に向かって続く数： 加藤文元、中井保行
https://blog.goo.ne.jp/ktonegaw/e/3d059b0a114b4bd712291a7fb81269e5
感想： NHK数学ミステリー白熱教室
https://blog.goo.ne.jp/ktonegaw/e/b0d53d030bf82e8016a1071fadb16063
数学の大統一に挑む：エドワード・フレンケル
https://blog.goo.ne.jp/ktonegaw/e/43ca100e56e15427613b009af55c8f7d
応援クリックをお願いします。
Image may be NSFW.
Clik here to view.
Image may be NSFW.Clik here to view.
Image may be NSFW.Clik here to view.
Image may be NSFW.
Clik here to view.
Image may be NSFW.Clik here to view.
Image may be NSFW.
Clik here to view.
Image may be NSFW.Clik here to view.
「宇宙と宇宙をつなぐ数学 IUT理論の衝撃： 加藤文元」（Kindle版）
Image may be NSFW.
Clik here to view.
はじめに
刊行によせて（望月新一：IUT理論提唱者、京都大学教授）
第1章 IUTショック
- 「イエス、グーグル！」
- 国際、銀河際、宇宙際
- 未来からやってきた論文
- 数学界の反応
- 共通の言語
- コミュニケーションパラダイム
- たし算とかけ算を分離する
- 「いざない」
- 最良のコミュニケーション
- IUT語
第2章 数学者の仕事
- 数学で新しいことができるのはなぜか？
- 数学が進歩するとは、どういうことなのか？
- 数学とは異種格闘技である！
- 論文の価値はなにで決まるのか？
- 数学は体力を使う学問である
- 「興味深い」ということ
- 理論はいかにして世界へ発信されるのか？
- 数学はお金がかかる学問である
- 数学のジャーナル
- 論文がアクセプトされるとはどういうことなのか？
- 紳士のゲーム
- そもそも人はなぜ数学するのか？
- 純粋と応用
- 楕円曲線とICカード
- ありふれたサクセスストーリー
- 数学の限りない可能性
第3章 宇宙際幾何学者
- 数学の変革
- 32歳で京大教授
- 焼肉とドラマ
- ディオファントス方程式
- 実効版モーデル予想
- タイヒミュラー理論
- 遠アーベル幾何学
- ホッジ・アラケロフ理論
- 自然であること
- アナロジー
第4章 たし算とかけ算
- 素数と素因数分解
- 根基
- ABCトリプル
- 例外的ABCトリプルとABC予想
- 強いABC予想
- その波及効果
- そもそも予想とはなにか？
- 予想はなぜ可能なのか？
- 気まぐれな素因数
- たし算的側面とかけ算的側面
- 素数が現れるタイミング
- たし算とかけ算の絡み合い
第5章 パズルのピース
- IUT理論の新しさ
- 数学の舞台
- ジグソーパズル
- 学校で教わる数学
- IUTパズル
- たし算とかけ算による正則構造
- 新しい柔軟性
- 入れ子宇宙
- 異なる舞台のピースをはめる
- テータリンク
第6章 対称性通信
- 複数の舞台で考える
- 舞台間の通信はどうするのか？
- 対称性
- 回転と鏡映
- 対称性による復元
- 復元ゲーム
- 対称性通信
- ひずみ
第7章 「行為」の計算
- 右向け右！
- 行為の合成
- 「動き」を計算する
- 「閉じている」ということ
- 記号の計算
- 記号化のご利益
- 対称性の群
- アーベル、非アーベル、遠アーベル
- 文字の置き換えゲーム
- 対称群
- 抽象的な群
- 対称性は壁を越える
- ガロア理論と「復元」
第8章 伝達・復元・ひずみ
- IUT理論がやろうとしていること
- 目指す不等式
- 異なる数学んお「舞台」のパズルのピース
- 対称性通信と計算
- テータ関数
- ひずみの計測
- 局所と大域
- 精密な同期
- まとめ
おわりにかえて 川上量生（株式会社ドワンゴ顧問）