[Set 59,319 on Mr. Cube root]Zoom
[Japanese]
Following the last time, today's example is about actual solution of Cube root using abacus.
Today's example is simple - basic 1/3-multiplication table method, root is 2-digits case and and we require 9 as root in the steps. You can check the Index page of all articles.
Cube root methods: Triple-root method, constant number method, 3a^2 method, 1/3-division method, 1/3-multiplication table method, 1/3-multiplication table alternative method, Multiplication-Subtraction method, 3-root^2 method, Mixing method, Exceed number method, Omission Method, etc.
Abacus steps to solve Cube root of 59,3192
(Answer is 39)
"1st group number" is the left most numbers in the 3-digits groups of the given number for cube root calculation. Number of groups is the number of digits of the Cube root.
59,319 -> (59|319): 59 is the 1st group number. The root digits is 2.
![]()
Step 1: Place 59319 on HIJKL.
![]()
Step 2: The 1st group is 59.
![]()
Step 3: Cube number ≦ 59 is 27=3^3. Place 3 on C as the 1st root.
![]()
Step 4: Subtract 3^3 from the 1st group 59. Place 59-3^3=32 on HI.
![]()
Step 5: Focus on 32319 on HIJKL.
![]()
Step 6: Divide 32319 by 3. Place 32319/3=10773 on HIJKL.
![]()
Step 7: Focus on 10 on HI.
![]()
Step 8: Repeat division by triple root 4 until 4th digits next to 1st root. 10/3=3 remainder 1. Place 3 on E.
![]()
Step 9: Place remainder 01 on HI.
![]()
Step 10: Divide 17 on IJ by current root 3. 17/3=5 remainder 2
![]()
Step 11: Place 5 on F.
![]()
Step 12: Place 02 on IJ.
![]()
Step 13: Divide 27 on JK by current root 3. 27/3=9 remainder 0
![]()
Step 14: Place 9 on G.
![]()
Step 15: Place 00 on JK.
![]()
Step 16: As the last digit of EFG equals to the last digit of current root C x3, we set 9 on D as 2nd root.
![]()
Step 17: Divide 35 on EF by current root 9. 35/9=3 remainder 8.
![]()
Step 18: Place 02 on EF.
![]()
Step 19: Place 89-2nd root^2=89-9^2=08 on FG.
![]()
Step 20: 08 on FG x 1st root 3 + 00 on JK. Place 3x8+0=24 on JK.
![]()
Step 21: Subtract 2nd root 9^3/3 from 243 on JKL. 243-9^3/3=0
![]()
Step 22: Place 000 on JKL.
![]()
Step 23: Cube root of 59319 is 39.
![]()
Final state: Answer 39
Abacus state transition. (Click to Zoom)
![]()
It is interesting to compare with the Triple-root method.
Next article is also 1/3-multiplication table method.
Related articles:
How to solve Cube root of 1729.03 using abacus? (Feynman v.s. Abacus man)
https://blog.goo.ne.jp/ktonegaw/e/cff5d6e7ecaa07230b9cc7af10b23aed
Index: Square root and Cube root using Abacus
https://blog.goo.ne.jp/ktonegaw/e/f62fb31b6a3a0417ec5d33591249451b
Cube root 59,319 using abacus (Triple-root method 4)
https://blog.goo.ne.jp/ktonegaw/e/e5d49843b3bb4aa289d1f4faebd879d3
Please place your mouse on the buttons and click one by one. These are blog ranking sites.
![にほんブログ村 科学ブログ 物理学へ]()
![人気ブログランキングへ]()
![]()
[Japanese]
Following the last time, today's example is about actual solution of Cube root using abacus.
Today's example is simple - basic 1/3-multiplication table method, root is 2-digits case and and we require 9 as root in the steps. You can check the Index page of all articles.
Cube root methods: Triple-root method, constant number method, 3a^2 method, 1/3-division method, 1/3-multiplication table method, 1/3-multiplication table alternative method, Multiplication-Subtraction method, 3-root^2 method, Mixing method, Exceed number method, Omission Method, etc.
Abacus steps to solve Cube root of 59,3192
(Answer is 39)
"1st group number" is the left most numbers in the 3-digits groups of the given number for cube root calculation. Number of groups is the number of digits of the Cube root.
59,319 -> (59|319): 59 is the 1st group number. The root digits is 2.
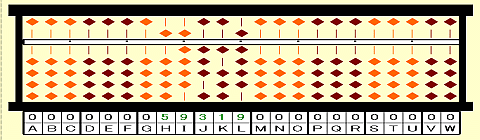
Step 1: Place 59319 on HIJKL.

Step 2: The 1st group is 59.
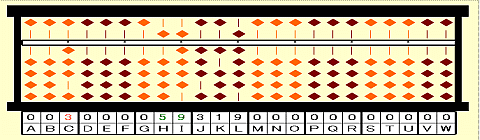
Step 3: Cube number ≦ 59 is 27=3^3. Place 3 on C as the 1st root.
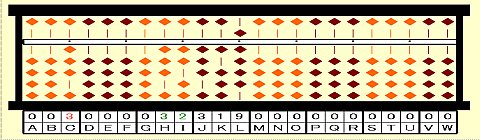
Step 4: Subtract 3^3 from the 1st group 59. Place 59-3^3=32 on HI.
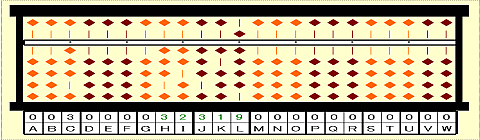
Step 5: Focus on 32319 on HIJKL.

Step 6: Divide 32319 by 3. Place 32319/3=10773 on HIJKL.

Step 7: Focus on 10 on HI.

Step 8: Repeat division by triple root 4 until 4th digits next to 1st root. 10/3=3 remainder 1. Place 3 on E.

Step 9: Place remainder 01 on HI.

Step 10: Divide 17 on IJ by current root 3. 17/3=5 remainder 2

Step 11: Place 5 on F.
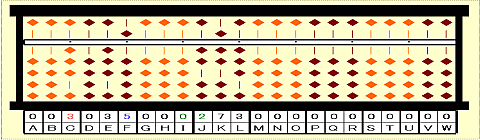
Step 12: Place 02 on IJ.

Step 13: Divide 27 on JK by current root 3. 27/3=9 remainder 0

Step 14: Place 9 on G.

Step 15: Place 00 on JK.

Step 16: As the last digit of EFG equals to the last digit of current root C x3, we set 9 on D as 2nd root.

Step 17: Divide 35 on EF by current root 9. 35/9=3 remainder 8.
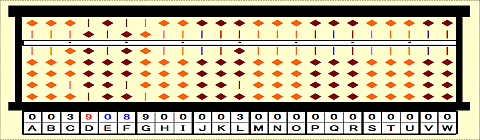
Step 18: Place 02 on EF.
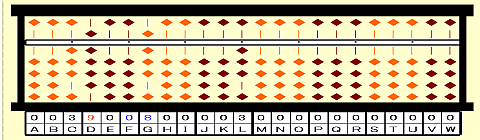
Step 19: Place 89-2nd root^2=89-9^2=08 on FG.

Step 20: 08 on FG x 1st root 3 + 00 on JK. Place 3x8+0=24 on JK.

Step 21: Subtract 2nd root 9^3/3 from 243 on JKL. 243-9^3/3=0
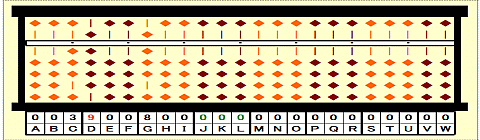
Step 22: Place 000 on JKL.
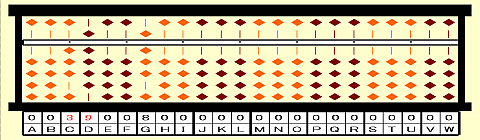
Step 23: Cube root of 59319 is 39.

Final state: Answer 39
Abacus state transition. (Click to Zoom)

It is interesting to compare with the Triple-root method.
Next article is also 1/3-multiplication table method.
Related articles:
How to solve Cube root of 1729.03 using abacus? (Feynman v.s. Abacus man)
https://blog.goo.ne.jp/ktonegaw/e/cff5d6e7ecaa07230b9cc7af10b23aed
Index: Square root and Cube root using Abacus
https://blog.goo.ne.jp/ktonegaw/e/f62fb31b6a3a0417ec5d33591249451b
Cube root 59,319 using abacus (Triple-root method 4)
https://blog.goo.ne.jp/ktonegaw/e/e5d49843b3bb4aa289d1f4faebd879d3
Please place your mouse on the buttons and click one by one. These are blog ranking sites.




















