[Set 421,875 on Mr. Cube root]Zoom
[Japanese]
Following the last time, today's example is about actual solution of Cube root using abacus.
Today's example is simple - basic 1/3-multiplication table method, root is 2-digits case. You can check the Index page of all articles.
Cube root methods: Triple-root method, constant number method, 3a^2 method, 1/3-division method, 1/3-multiplication table method, 1/3-multiplication table alternative method, Multiplication-Subtraction method, 3-root^2 method, Mixing method, Exceed number method, Omission Method, etc.
Abacus steps to solve Cube root of 421,875
(Answer is 75)
"1st group number" is the left most numbers in the 3-digits groups of the given number for cube root calculation. Number of groups is the number of digits of the Cube root.
421,875 -> (421|875): 421 is the 1st group number. The root digits is 2.
![]()
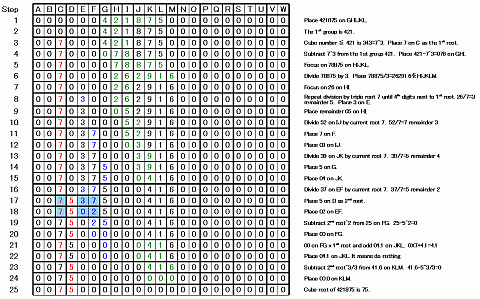
Step 1: Place 421875 on GHIJKL.
![]()
Step 2: The 1st group is 421.
![]()
Step 3: Cube number ≦ 421 is 343=7^3. Place 7 on C as the 1st root.
![]()
Step 4: Subtract 7^3 from the 1st group 421. Place 421-7^3=078 on GHI.
![]()
Step 5: Focus on 78875 on HIJKL.
![]()
Step 6: Divide 78875 by 3. Place 78875/3=26291.6 on HIJKLM.
![]()
Step 7: Focus on 26 on HI.
![]()
Step 8: Repeat division by triple root 7 until 4th digits next to 1st root. 26/7=3 remainder 5. Place 3 on E.
![]()
Step 9: Place remainder 05 on HI.
![]()
Step 10: Divide 52 on IJ by current root 7. 52/7=7 remainder 3
![]()
Step 11: Place 7 on F.
![]()
Step 12: Place 03 on IJ.
![]()
Step 13: Divide 39 on JK by current root 7. 39/7=5 remainder 4
![]()
Step 14: Place 5 on G.
![]()
Step 15: Place 04 on JK.
![]()
Step 16: Divide 37 on EF by current root 7. 37/7=5 remainder 2
![]()
Step 17: Place 5 on D as 2nd root.
![]()
Step 18: Place 02 on EF.
![]()
Step 19: Subtract 2nd root^2 from 25 on FG. 25-5^2=0
![]()
Step 20: Place 00 on FG.
![]()
Step 21: 00 on FG x 1st root and add 04.1 on JKL. 0X7+4.1=4.1
![]()
Step 22: Place 04.1 on JKL. It means do nothing.
![]()
Step 23: Subtract 2nd root^3/3 from 41.6 on KLM. 41.6-5^3/3=0
![]()
Step 24: Place 00.0 on KLM.
![]()
Step 25: Cube root of 421875 is 75.
![]()
Final state: Answer 75
Abacus state transition. (Click to Zoom)
![]()
It is interesting to compare with the Triple-root method.
Next article is also 1/3-multiplication table method.
Related articles:
How to solve Cube root of 1729.03 using abacus? (Feynman v.s. Abacus man)
http://blog.goo.ne.jp/ktonegaw/e/cff5d6e7ecaa07230b9cc7af10b23aed
Index: Square root and Cube root using Abacus
http://blog.goo.ne.jp/ktonegaw/e/f62fb31b6a3a0417ec5d33591249451b
Cube root 421,875 using abacus (Triple-root method 1)
http://blog.goo.ne.jp/ktonegaw/e/6a4c5516b2ede10271ac7e718daa4815
Please place your mouse on the buttons and click one by one. These are blog ranking sites.
![にほんブログ村 科学ブログ 物理学へ]()
![人気ブログランキングへ]()
![]()
[Japanese]
Following the last time, today's example is about actual solution of Cube root using abacus.
Today's example is simple - basic 1/3-multiplication table method, root is 2-digits case. You can check the Index page of all articles.
Cube root methods: Triple-root method, constant number method, 3a^2 method, 1/3-division method, 1/3-multiplication table method, 1/3-multiplication table alternative method, Multiplication-Subtraction method, 3-root^2 method, Mixing method, Exceed number method, Omission Method, etc.
Abacus steps to solve Cube root of 421,875
(Answer is 75)
"1st group number" is the left most numbers in the 3-digits groups of the given number for cube root calculation. Number of groups is the number of digits of the Cube root.
421,875 -> (421|875): 421 is the 1st group number. The root digits is 2.
Step 1: Place 421875 on GHIJKL.
Step 2: The 1st group is 421.
Step 3: Cube number ≦ 421 is 343=7^3. Place 7 on C as the 1st root.
Step 4: Subtract 7^3 from the 1st group 421. Place 421-7^3=078 on GHI.
Step 5: Focus on 78875 on HIJKL.
Step 6: Divide 78875 by 3. Place 78875/3=26291.6 on HIJKLM.
Step 7: Focus on 26 on HI.
Step 8: Repeat division by triple root 7 until 4th digits next to 1st root. 26/7=3 remainder 5. Place 3 on E.
Step 9: Place remainder 05 on HI.
Step 10: Divide 52 on IJ by current root 7. 52/7=7 remainder 3
Step 11: Place 7 on F.
Step 12: Place 03 on IJ.
Step 13: Divide 39 on JK by current root 7. 39/7=5 remainder 4
Step 14: Place 5 on G.
Step 15: Place 04 on JK.
Step 16: Divide 37 on EF by current root 7. 37/7=5 remainder 2
Step 17: Place 5 on D as 2nd root.
Step 18: Place 02 on EF.
Step 19: Subtract 2nd root^2 from 25 on FG. 25-5^2=0
Step 20: Place 00 on FG.
Step 21: 00 on FG x 1st root and add 04.1 on JKL. 0X7+4.1=4.1
Step 22: Place 04.1 on JKL. It means do nothing.
Step 23: Subtract 2nd root^3/3 from 41.6 on KLM. 41.6-5^3/3=0
Step 24: Place 00.0 on KLM.
Step 25: Cube root of 421875 is 75.
Final state: Answer 75
Abacus state transition. (Click to Zoom)
It is interesting to compare with the Triple-root method.
Next article is also 1/3-multiplication table method.
Related articles:
How to solve Cube root of 1729.03 using abacus? (Feynman v.s. Abacus man)
http://blog.goo.ne.jp/ktonegaw/e/cff5d6e7ecaa07230b9cc7af10b23aed
Index: Square root and Cube root using Abacus
http://blog.goo.ne.jp/ktonegaw/e/f62fb31b6a3a0417ec5d33591249451b
Cube root 421,875 using abacus (Triple-root method 1)
http://blog.goo.ne.jp/ktonegaw/e/6a4c5516b2ede10271ac7e718daa4815
Please place your mouse on the buttons and click one by one. These are blog ranking sites.
