[Set 11,943,936 on Mr. Square root]Zoom
[Japanese]
We will continue from where we ended in the last article, the article shows actual solutions to calculate Square root using abacus. Today's example is simple - basic Double-root method, root is 4-digits case.. Please check the Theory page for your reference.
Square root methods: Double-root method, Double-root alternative method, half-multiplication table method, half-multiplication table alternative method, multiplication-subtraction method, constant number method, etc.
Abacus steps to solve Square root of 11,943,936
(Answer is 3,456)
"1st group number" is the left most numbers in the 2-digits groups of the given number for square root calculation. Number of groups is the number of digits of the Square root.
11,943,936 -> (11|94|39|36) : 11 is the 1st group number. The root digits is 4.
Image may be NSFW.
Clik here to view.
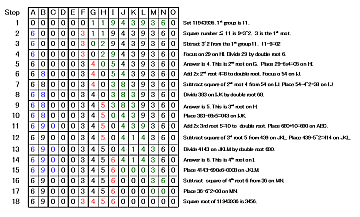
Step 1: Set 11943936. 1st group is 11.
Image may be NSFW.
Clik here to view.
Step 2: Square number smaller than or equal to 11 is 9=3^2. 3 is the 1st root.
Image may be NSFW.
Clik here to view.
Step 3: Sbtract 3^2 from the 1st group 11. 11-9=02
Image may be NSFW.
Clik here to view.
Step 4: Focus on 29 on HI. Divide 29 by double root 6.
Image may be NSFW.
Clik here to view.
Step 5: Answer is 4. This is 2nd root on G. Place 29-6x4=05 on HI.
Image may be NSFW.
Clik here to view.
Step 6: Add 2x 2nd root 4=8 to double root. Focus o 54 on IJ.
Image may be NSFW.
Clik here to view.
Step 7: Subtract square of 2nd root 4 from 54 on IJ. Place 54-4^2=38 on IJ.
Image may be NSFW.
Clik here to view.
Step 8: Divide 383 on IJK by double root 68.
Image may be NSFW.
Clik here to view.
Step 9: Answer is 5. This is 3rd root on H.
Image may be NSFW.
Clik here to view.
Step 10: Place 383-68x5=043 on IJK.
Image may be NSFW.
Clik here to view.
Step 11: Add 2x 3rd root 5=10 to double root. Place 680+10=690 on ABC.
Image may be NSFW.
Clik here to view.
Step 12: Subtract square of 3rd root 5 from 439 on JKL. Place 439-5^2=414 on JKL.
Image may be NSFW.
Clik here to view.
Step 13: Divide 4143 on JKLM by double root 690.
Image may be NSFW.
Clik here to view.
Step 14: Answer is 6. This is 4th root on I.
Image may be NSFW.
Clik here to view.
Step 15: Place 4143-690x6=0003 on JKLM.
Image may be NSFW.
Clik here to view.
Step 16: Subtract square of 4th root 6 from 36 on MN.
Image may be NSFW.
Clik here to view.
Step 17: Place 36-6^2=00 on MN.
Image may be NSFW.
Clik here to view.
Step 18: Square root of 11943936 is 3456.
Image may be NSFW.
Clik here to view.![]()
Final state: Answer 3456
Abacus state transition. (Click to Zoom)
Image may be NSFW.
Clik here to view.![]()
Next article is also about Double-root method.
Related articles:
How to solve Cube root of 1729.03 using abacus? (Feynman v.s. Abacus man)
http://blog.goo.ne.jp/ktonegaw/e/cff5d6e7ecaa07230b9cc7af10b23aed
Please place your mouse on the buttons and click one by one. These are blog ranking sites.
Image may be NSFW.
Clik here to view.![にほんブログ村 科学ブログ 物理学へ]() Image may be NSFW.
Image may be NSFW.
Clik here to view.![人気ブログランキングへ]() Image may be NSFW.
Image may be NSFW.
Clik here to view.![]()
[Japanese]
We will continue from where we ended in the last article, the article shows actual solutions to calculate Square root using abacus. Today's example is simple - basic Double-root method, root is 4-digits case.. Please check the Theory page for your reference.
Square root methods: Double-root method, Double-root alternative method, half-multiplication table method, half-multiplication table alternative method, multiplication-subtraction method, constant number method, etc.
Abacus steps to solve Square root of 11,943,936
(Answer is 3,456)
"1st group number" is the left most numbers in the 2-digits groups of the given number for square root calculation. Number of groups is the number of digits of the Square root.
11,943,936 -> (11|94|39|36) : 11 is the 1st group number. The root digits is 4.
Image may be NSFW.
Clik here to view.

Step 1: Set 11943936. 1st group is 11.
Image may be NSFW.
Clik here to view.

Step 2: Square number smaller than or equal to 11 is 9=3^2. 3 is the 1st root.
Image may be NSFW.
Clik here to view.

Step 3: Sbtract 3^2 from the 1st group 11. 11-9=02
Image may be NSFW.
Clik here to view.

Step 4: Focus on 29 on HI. Divide 29 by double root 6.
Image may be NSFW.
Clik here to view.

Step 5: Answer is 4. This is 2nd root on G. Place 29-6x4=05 on HI.
Image may be NSFW.
Clik here to view.

Step 6: Add 2x 2nd root 4=8 to double root. Focus o 54 on IJ.
Image may be NSFW.
Clik here to view.

Step 7: Subtract square of 2nd root 4 from 54 on IJ. Place 54-4^2=38 on IJ.
Image may be NSFW.
Clik here to view.

Step 8: Divide 383 on IJK by double root 68.
Image may be NSFW.
Clik here to view.

Step 9: Answer is 5. This is 3rd root on H.
Image may be NSFW.
Clik here to view.

Step 10: Place 383-68x5=043 on IJK.
Image may be NSFW.
Clik here to view.

Step 11: Add 2x 3rd root 5=10 to double root. Place 680+10=690 on ABC.
Image may be NSFW.
Clik here to view.

Step 12: Subtract square of 3rd root 5 from 439 on JKL. Place 439-5^2=414 on JKL.
Image may be NSFW.
Clik here to view.

Step 13: Divide 4143 on JKLM by double root 690.
Image may be NSFW.
Clik here to view.

Step 14: Answer is 6. This is 4th root on I.
Image may be NSFW.
Clik here to view.

Step 15: Place 4143-690x6=0003 on JKLM.
Image may be NSFW.
Clik here to view.

Step 16: Subtract square of 4th root 6 from 36 on MN.
Image may be NSFW.
Clik here to view.

Step 17: Place 36-6^2=00 on MN.
Image may be NSFW.
Clik here to view.

Step 18: Square root of 11943936 is 3456.
Image may be NSFW.
Clik here to view.

Final state: Answer 3456
Abacus state transition. (Click to Zoom)
Image may be NSFW.
Clik here to view.
Next article is also about Double-root method.
Related articles:
How to solve Cube root of 1729.03 using abacus? (Feynman v.s. Abacus man)
http://blog.goo.ne.jp/ktonegaw/e/cff5d6e7ecaa07230b9cc7af10b23aed
Please place your mouse on the buttons and click one by one. These are blog ranking sites.
Image may be NSFW.
Clik here to view.
 Image may be NSFW.
Image may be NSFW.Clik here to view.
 Image may be NSFW.
Image may be NSFW.Clik here to view.
