「クラウド量子計算入門―IBMの量子シミュレーションと量子コンピュータ: 中山茂」
内容紹介:
IBMから提供される無料の量子計算プラットフォームを体験する!大学での講義を想定した豊富な例題、演習、実験で理解を深める。16の量子実験を通して、量子アルゴリズムを学び、量子シミュレーションで実行する。
2016年10月10日刊行、331ページ。
著者について:
中山茂(なかやましげる)
京都生まれ。京都大学大学院工学研究科博士課程修了後、上智大学、英国Reading大学、京都工芸繊維大学、兵庫教育大学、英国Oxford大学、鹿児島大学を経て、2014年に定年退職。京都大学工学博士。
理数系書籍のレビュー記事は本書で329冊目。
IBM Quantum Experience(入口)
http://www.research.ibm.com/quantum/
その後、ヒマを見つけては本書を頼りに量子コンピュータで実験を繰り返していた。うまくいく実験もあれば、できない実験もあった。行列とケット・ベクトルの計算もできるようになったし、章別に紹介されているアルゴリズムも理解できた。当初の目的は果たせたのだと思う。
さて、紹介記事を書く段になって困ってしまった。いくつも実験をしたのでどれを取り上げて紹介したらよいか迷うのだ。全部紹介するのはもちろん無理で、かといって本の真ん中あたりのアルゴリズムを紹介するのも難しい。章を追うごとに前の章の結果を使った形で次のアルゴリズムが紹介されているからだ。途中の章をいきなり紹介したところでブログの読者には何のことかわからなくなる。
しばらく考えて思いついたのが「量子現象の基礎的な原理を象徴的に示している実験」に限定して紹介するということだ。量子アルゴリズムにも興味があるが、自然科学の基本原理により強い興味を持っている僕には「萌え度」が高まるからだ。
つまり「基本的な量子ゲートの紹介」、「量子の絡み合い(エンタングルメント)」、「量子テレポーテーション」の3つをこの記事で紹介することにした。基本的な量子ゲートのひとつ「アダマールゲート」が生成する量子の重ね合わせ、そして「トフォリゲート」が可能にする量子の絡み合いの2つが古典コンピュータにはない利点を量子コンピュータに与えている原理なのである。
差し当たり本書の章立てはこうなっている。
第1章 はじめてのIBMの5量子ビット実験
第2章 パウリゲートの量子実験
第3章 アダマールゲートの量子実験
第4章 位相シフトゲートの量子実験
第5章 制御NOTゲートの量子実験
第6章 トフォリゲートの量子実験
第7章 ドイチ・ジョザ問題の量子実験
第8章 ベルンシュタイン・ヴァジラニ問題の量子実験
第9章 サイモン問題の量子実験
第10章 量子フーリエ変換の量子実験
第11章 位相・固有値・位数推定問題の量子実験
第12章 ショアの素因数分解問題の量子実験
第13章 グローバーの探索問題の量子実験
第14章 量子非局所性の量子実験
第15章 量子通信の量子実験
第16章 量子エラーとスタビライザー測定
第17章 量子誤り訂正の量子実験
第6章までは基本的な量子ゲートの解説と実験にあてられている。そして第7章から第17章までは量子アルゴリズムの解説と実験だ。
古典コンピュータではANDゲート、ORゲート、NOTゲート、NORゲートなどが用意されていて、これらを組み合わせて論理回路を構成する。原理的にはANDゲートとNOTゲートだけ、あるいはNORゲートだけを使ってあらゆる論理回路を作ることができる。その最小構成を万能ゲートと呼んでいる。
基本的な量子ゲート
量子コンピュータにも万能ゲートを考えることができるわけだが、公開されているIBMの量子コンピュータでは次のようなゲートが用意されている。
![]()
グループ別に紹介しよう。
まず、恒等演算を行うidゲート、そしてX、Y、Zであらわされるパウリゲートだ。
![]()
たとえば状態0や状態1を表すケット・ベクトルに対してXやZの演算を行うと演算後の状態ベクトルは次のように計算される。ちなみにXゲートが古典コンピュータのNOTゲートに対応している。
![]()
![]()
Hゲートはアダマールゲートと呼ばれ、「重ね合わせ状態」を作るために使われる。行列では次のようにあらわされる。量子コンピュータが現在のスパコンをはるかに凌ぐ速度で計算できるのも量子の重ね合わせ状態を使うからである。
![]()
SとTそしてそれらにタガーがついたものは位相シフトゲートと呼ばれ、次のような行列であらわされる。
![]()
そして〇の中に十字が描かれたアイコンであらわされるのが制御NOTゲートだ。CNOTゲートと書かれることもある。このゲートを使うと「絡み合い状態」を作ることができる。本書では絡み合い状態のことを「もつれ状態」と呼んでいる。量子通信(つまり量子テレポーテーション)はこのゲートを使って実現される。
![]()
第6章で紹介されるトフォリゲートは制御NOTゲートを2つ使って構成する「制御制御NOTゲート(CCNOTゲート)」のことである。制御NOTゲートが2粒子の絡み合い状態を作るのに対し、トフォリゲートでは3粒子の絡み合い状態を作ることができる。そしてゲートを増やせば多粒子の絡み合い状態を作れる。
実験1:量子の絡み合い
この実験は前回の記事で紹介した。本書の第14章「量子非局所性の量子実験」で説明されている「GHZ状態のZZZ測定」という実験のことだ。
これは多粒子(この場合は3粒子)の絡み合い状態である「GHZ状態」を用いて量子非局所性状態を証明するための実験だ。2粒子系の「ベル状態」よりも3粒子系の「GHZ状態」を用いたほうが局所実在性の破れが強く出て、ベル状態の局所実在性の確率論的な破れよりも、GHZ状態の局所実在性のほうが決定論的な破れがあるとされている。
この実験でアインシュタインが「不可解な遠隔作用」、「EPRパラドックス」として忌み嫌った状況が量子コンピュータ内に再現できたことになる。
量子回路(アルゴリズム):第6章で解説されているトフォリゲートが使われている。
![]()
実験結果(クリックで拡大)
![]()
実験2:量子テレポーテーション
そもそもこのブログが物理ブログになったのは量子テレポーテーションの実験が成功していることに衝撃を受けたのがきっかけだ。本書の第15章「量子通信の量子実験」とは量子テレポーテーション、量子転送のことである。(参考記事:「テレポーテーションは実現している。(リンク集)」)
IBMの量子コンピュータでは状態0、状態1のようなシンプルな状態の量子転送(つまり通常の意味での量子テレポーテーション)だけでなく、重ね合わせ状態の量子転送や絡み合い状態の量子転送を行うことができる。
ここでは重ね合わせ状態の量子転送実験を紹介しよう。
転送するのはXゲートとHゲートを使って生成した重ね合わせ状態だ。
![]()
つまり量子ビット0にあるこの状態を転送することになる。
![]()
そのまま測定すると、このように量子ビット0は状態0と状態1が半々の重ね合わせの状態であることがわかる。棒グラフの下の5つの数字のいちばん右が量子ビット0である。
![]()
量子ビット0の重ね合わせ状態を量子ビット2に転送するのがこの実験だ。
量子転送では量子の絡み合いを利用するから量子転送ゲートの中にトフォリゲートがあるのがおわかりいただけるだろう。赤枠で囲った部分が量子転送ゲートである。測定アイコンは量子ビット2の量子転送ゲートの後ろに置く。
量子回路(アルゴリズム)
![]()
実験結果
![]()
量子ビット2(5つ並んでいる数字の右から3番目)がもとの量子状態と同じく状態0と状態1が半々の重ね合わせの状態であることがわかるだろう。つまり重ね合わせ状態の転送に成功したことがわかるのだ。量子ビット0から量子ビット2へのほんのわずかな距離の量子テレポーテーションである。
5つの量子ビットが搭載されたIBMの量子コンピュータ心臓部
![]()
その他の感想、考えたこと
ファインマン先生は著書「ファインマン計算機科学:ファインマン, A.ヘイ, R.アレン」で量子コンピュータのアイデアを公表したが、それは原子サイズの素子を使ったコンピュータ、可逆計算ができるコンピュータという意味においてである。重ね合わせ状態を使った超超高速並列計算に関して言えばファインマン先生は気が付いていなかった。この点において量子コンピュータの本当の発案者はドイチェ・ジョザのアルゴリズムを考案者のうちのひとり、ドイチェである。
量子アルゴリズムの研究は始まったばかりだ。本書には「古典コンピュータのアルゴリズムのすべてが量子コンピュータで実現できるわけではない。」と書かれている。汎用量子コンピュータができるかどうかは原理的な問題なのか、研究を続ければ実現可能なのかは僕にはわからないが、後者であることを願いたい。「量子プログラミングの基礎: イン・ミンシェン」という本が出たばかりだが、現在のコンピュータのようにプログラミング言語を使って自在に開発を行えるような量子コンピュータが実現するのはもう少し先のようである。
量子アルゴリズムは本書を読みながらやっと理解できた。自分でアルゴリズムを考え量子ゲートを組み上げることはできないことを実感した。僕は古典コンピュータの論理ゲートを使ったデジタル回路さえ作ったことがないのだから、当然と言えば当然である。(参考記事:「電卓を作りたいという妄想」)
また、IBMの量子コンピュータで公開されているUser Guideだけ読んで量子アルゴリズムの実験をして遊ぶのも初心者には無理だ。専門書で学ぶか本書のような解説本を参照しながらであれば、高校生でも実験を楽しむことができる。ぜひ、ご自身で試してみてほしい。
ブログを始めて12年。現実の世界、ニューヨークに置かれた量子コンピュータを使って僕はようやく自分で量子テレポーテーションの実験を行なったことになる。小さいながらも今日は記念日だ。
著者の中山先生は次の本も2年前にお書きになっている。目次を見ると本書の理論的側面を学べる本だということがわかる。合わせてお読みになるとよいだろう。Kindle版は固定レイアウトなのでご注意。
「量子アルゴリズム:中山茂」(Kindle版)(目次)
![]()
量子コンピュータ関連の本: Amazonで検索
関連記事:
発売情報: クラウド量子計算入門: 中山茂
http://blog.goo.ne.jp/ktonegaw/e/d360b69100fbe723c5b9410dbf3f5f4d
量子コンピュータ入門:宮野健次郎、古澤明
http://blog.goo.ne.jp/ktonegaw/e/ef75709187cf4b35a12f2d9fdf73a320
ファインマン計算機科学:ファインマン, A.ヘイ, R.アレン
http://blog.goo.ne.jp/ktonegaw/e/4f7f453019fd463ed2bfdeaa7b288d79
量子コンピュータ、量子アルゴリズムを学びたい高校生のために
http://blog.goo.ne.jp/ktonegaw/e/1b2940b648bda682aa27192eb8261972
発売情報:量子プログラミングの基礎: イン・ミンシェン
http://blog.goo.ne.jp/ktonegaw/e/27e4d9a10982d4d69c0029fc4c801708
関連ページ:
IBMの量子コンピュータを使ってみた
http://kadora.hatenablog.com/entry/2016/09/10/230116
従来のPCの1億倍高速な量子コンピューターはどのような仕組みで動いて物理的限界を突破しているのかがわかるムービー
http://gigazine.net/news/20151210-quantum-computers-explained/
わかりやすい量子コンピュータ
http://matome.naver.jp/odai/2133630808407668301
「ITエンジニアのための量子コンピュータ入門」連載一覧
http://codezine.jp/article/corner/629
量子力学の反常識が創りだす量子コンピューティングの世界
~量子コンピュータの頭脳としての量子アルゴリズム~
http://www.kyoto-su.ac.jp/project/st/st14_03.html
米メリーランド大学、世界初となる「汎用計算可能量子コンピュータ」モジュールを開発
http://pc.watch.impress.co.jp/docs/news/1014034.html
関連動画:
量子論、量子テレポーテーション、量子コンピュータ
量子の制御とコンピュータ(量子コンピュータの原理の概要説明)
量子コンピュータ授業 #1(15回の講義。本書で解説される量子ゲート、量子アルゴリズムのほとんどを学ぶことができる。)
15回の講義内容
![]()
ブログ執筆のはげみになりますので、1つずつ応援クリックをお願いします。
![にほんブログ村 科学ブログ 物理学へ]()
![人気ブログランキングへ]()
![]()
とね日記は長年放置されている科学ブログランキングの不正クリックに対し、次のランキングサイトには適切な運営を期待します。
「FC2自然科学ブログランキング」:不正の例1 例2
「にほんブログ村、科学ブログランキング」:New-不正の例1
(不正クリックブログの見分け方)
![]()
![]()
![]()
![]()
「クラウド量子計算入門―IBMの量子シミュレーションと量子コンピュータ: 中山茂」
![]()
第1章 はじめてのIBMの5量子ビット実験
1.1 IBMの量子シミュレーションと量子コンピュータ実験
1.2 クラウド量子計算に期待されること
1.3 クラウド量子計算への歩み
1.4 はじめてのIBMのクラウド量子計算
1.5 はじめてのIBMの量子シミュレータ
1.6 はじめてのIBMの量子コンピュータ
第2章 パウリゲートの量子実験
2.1 パウリゲートとは
2.2 恒等ゲートとパウリゲートを使った量子シミュレータ実験
第3章 アダマールゲートの量子実験
3.1 アダマール変換とは
3.2 アダマール演算による量子シミュレータ実験
第4章 位相シフトゲートの量子実験
4.1 位相シフト演算とは
4.2 T深度による量子実験
第5章 制御NOTゲートの量子実験
5.1 制御NOTゲートと重ね合わせ状態
5.2 制御NOTゲートによるもつれ状態生成
5.3 制御NOTゲートにおけるパウリ演算子
5.4 制御NOTゲートによる交換ゲート
5.5 制御Uゲートの生成
第6章 トフォリゲートの量子実験
6.1 3量子ビットのもつれ状態
6.2 トフォリゲートの量子実験
6.3 フレッドキンゲートの量子実験
第7章 ドイチ・ジョザ問題の量子実験
7.1 ドイチ問題の量子実験
7.2 ドイチ・ジョザ問題の量子実験
第8章 ベルンシュタイン・ヴァジラニ問題の量子実験
8.1 関数f(x)=x・aの定数aを求めるベルンシュタイン・ヴァジラニ問題
8.2 n=1のベルンシュタイン・ヴァジラニ問題
8.3 n=2のベルンシュタイン・ヴァジラニ問題
8.4 n=3のベルンシュタイン・ヴァジラニ問題
第9章 サイモン問題の量子実験
9.1 サイモン問題とは
9.2 n=2のサイモン問題の量子実験
第10章 量子フーリエ変換の量子実験
10.1 量子フーリエ変換の定義
10.2 量子フーリエ変換に必要な制御Sゲートの作成
10.3 量子フーリエ変換ゲートの実装
10.4 逆量子フーリエ変換ゲート
10.5 量子フーリエ変換によるシフト不変性
第11章 位相・固有値・位数推定問題の量子実験
11.1 位相推定問題の量子実験
11.2 ユニタリ変換の固有値推定アルゴリズムの量子実験
11.3 位数発見アルゴリズムの量子実験
第12章 ショアの素因数分解問題の量子実験
12.1 因数分解とユークリッドの互除法
12.2 ショアの素因数分解アルゴリズム
12.3 ショアの素因数分解のための量子回路
第13章 グローバーの探索問題の量子実験
13.1 グローバーの探索問題とは
13.2 グローバーの振幅増幅手法の量子回路
第14章 量子非局所性の量子実験
14.1 量子非局所性とCHSH不等式
14.2 GHZ状態の量子非局所性実験
第15章 量子通信の量子実験
15.1 量子高密度符号
15.2 量子転送
第16章 量子エラーとスタビライザー測定
16.1 量子エラーとシンドローム診断
16.2 ビットパリティ識別
16.3 符号パリティ識別
第17章 量子誤り訂正の量子実験
17.1 量子誤り訂正のための符号化と複合化
17.2 量子誤り訂正ゲート
内容紹介:
IBMから提供される無料の量子計算プラットフォームを体験する!大学での講義を想定した豊富な例題、演習、実験で理解を深める。16の量子実験を通して、量子アルゴリズムを学び、量子シミュレーションで実行する。
2016年10月10日刊行、331ページ。
著者について:
中山茂(なかやましげる)
京都生まれ。京都大学大学院工学研究科博士課程修了後、上智大学、英国Reading大学、京都工芸繊維大学、兵庫教育大学、英国Oxford大学、鹿児島大学を経て、2014年に定年退職。京都大学工学博士。
理数系書籍のレビュー記事は本書で329冊目。
IBM Quantum Experience(入口)
http://www.research.ibm.com/quantum/
その後、ヒマを見つけては本書を頼りに量子コンピュータで実験を繰り返していた。うまくいく実験もあれば、できない実験もあった。行列とケット・ベクトルの計算もできるようになったし、章別に紹介されているアルゴリズムも理解できた。当初の目的は果たせたのだと思う。
さて、紹介記事を書く段になって困ってしまった。いくつも実験をしたのでどれを取り上げて紹介したらよいか迷うのだ。全部紹介するのはもちろん無理で、かといって本の真ん中あたりのアルゴリズムを紹介するのも難しい。章を追うごとに前の章の結果を使った形で次のアルゴリズムが紹介されているからだ。途中の章をいきなり紹介したところでブログの読者には何のことかわからなくなる。
しばらく考えて思いついたのが「量子現象の基礎的な原理を象徴的に示している実験」に限定して紹介するということだ。量子アルゴリズムにも興味があるが、自然科学の基本原理により強い興味を持っている僕には「萌え度」が高まるからだ。
つまり「基本的な量子ゲートの紹介」、「量子の絡み合い(エンタングルメント)」、「量子テレポーテーション」の3つをこの記事で紹介することにした。基本的な量子ゲートのひとつ「アダマールゲート」が生成する量子の重ね合わせ、そして「トフォリゲート」が可能にする量子の絡み合いの2つが古典コンピュータにはない利点を量子コンピュータに与えている原理なのである。
差し当たり本書の章立てはこうなっている。
第1章 はじめてのIBMの5量子ビット実験
第2章 パウリゲートの量子実験
第3章 アダマールゲートの量子実験
第4章 位相シフトゲートの量子実験
第5章 制御NOTゲートの量子実験
第6章 トフォリゲートの量子実験
第7章 ドイチ・ジョザ問題の量子実験
第8章 ベルンシュタイン・ヴァジラニ問題の量子実験
第9章 サイモン問題の量子実験
第10章 量子フーリエ変換の量子実験
第11章 位相・固有値・位数推定問題の量子実験
第12章 ショアの素因数分解問題の量子実験
第13章 グローバーの探索問題の量子実験
第14章 量子非局所性の量子実験
第15章 量子通信の量子実験
第16章 量子エラーとスタビライザー測定
第17章 量子誤り訂正の量子実験
第6章までは基本的な量子ゲートの解説と実験にあてられている。そして第7章から第17章までは量子アルゴリズムの解説と実験だ。
古典コンピュータではANDゲート、ORゲート、NOTゲート、NORゲートなどが用意されていて、これらを組み合わせて論理回路を構成する。原理的にはANDゲートとNOTゲートだけ、あるいはNORゲートだけを使ってあらゆる論理回路を作ることができる。その最小構成を万能ゲートと呼んでいる。
基本的な量子ゲート
量子コンピュータにも万能ゲートを考えることができるわけだが、公開されているIBMの量子コンピュータでは次のようなゲートが用意されている。

グループ別に紹介しよう。
まず、恒等演算を行うidゲート、そしてX、Y、Zであらわされるパウリゲートだ。

たとえば状態0や状態1を表すケット・ベクトルに対してXやZの演算を行うと演算後の状態ベクトルは次のように計算される。ちなみにXゲートが古典コンピュータのNOTゲートに対応している。


Hゲートはアダマールゲートと呼ばれ、「重ね合わせ状態」を作るために使われる。行列では次のようにあらわされる。量子コンピュータが現在のスパコンをはるかに凌ぐ速度で計算できるのも量子の重ね合わせ状態を使うからである。

SとTそしてそれらにタガーがついたものは位相シフトゲートと呼ばれ、次のような行列であらわされる。

そして〇の中に十字が描かれたアイコンであらわされるのが制御NOTゲートだ。CNOTゲートと書かれることもある。このゲートを使うと「絡み合い状態」を作ることができる。本書では絡み合い状態のことを「もつれ状態」と呼んでいる。量子通信(つまり量子テレポーテーション)はこのゲートを使って実現される。

第6章で紹介されるトフォリゲートは制御NOTゲートを2つ使って構成する「制御制御NOTゲート(CCNOTゲート)」のことである。制御NOTゲートが2粒子の絡み合い状態を作るのに対し、トフォリゲートでは3粒子の絡み合い状態を作ることができる。そしてゲートを増やせば多粒子の絡み合い状態を作れる。
実験1:量子の絡み合い
この実験は前回の記事で紹介した。本書の第14章「量子非局所性の量子実験」で説明されている「GHZ状態のZZZ測定」という実験のことだ。
これは多粒子(この場合は3粒子)の絡み合い状態である「GHZ状態」を用いて量子非局所性状態を証明するための実験だ。2粒子系の「ベル状態」よりも3粒子系の「GHZ状態」を用いたほうが局所実在性の破れが強く出て、ベル状態の局所実在性の確率論的な破れよりも、GHZ状態の局所実在性のほうが決定論的な破れがあるとされている。
この実験でアインシュタインが「不可解な遠隔作用」、「EPRパラドックス」として忌み嫌った状況が量子コンピュータ内に再現できたことになる。
量子回路(アルゴリズム):第6章で解説されているトフォリゲートが使われている。

実験結果(クリックで拡大)

実験2:量子テレポーテーション
そもそもこのブログが物理ブログになったのは量子テレポーテーションの実験が成功していることに衝撃を受けたのがきっかけだ。本書の第15章「量子通信の量子実験」とは量子テレポーテーション、量子転送のことである。(参考記事:「テレポーテーションは実現している。(リンク集)」)
IBMの量子コンピュータでは状態0、状態1のようなシンプルな状態の量子転送(つまり通常の意味での量子テレポーテーション)だけでなく、重ね合わせ状態の量子転送や絡み合い状態の量子転送を行うことができる。
ここでは重ね合わせ状態の量子転送実験を紹介しよう。
転送するのはXゲートとHゲートを使って生成した重ね合わせ状態だ。

つまり量子ビット0にあるこの状態を転送することになる。

そのまま測定すると、このように量子ビット0は状態0と状態1が半々の重ね合わせの状態であることがわかる。棒グラフの下の5つの数字のいちばん右が量子ビット0である。

量子ビット0の重ね合わせ状態を量子ビット2に転送するのがこの実験だ。
量子転送では量子の絡み合いを利用するから量子転送ゲートの中にトフォリゲートがあるのがおわかりいただけるだろう。赤枠で囲った部分が量子転送ゲートである。測定アイコンは量子ビット2の量子転送ゲートの後ろに置く。
量子回路(アルゴリズム)

実験結果
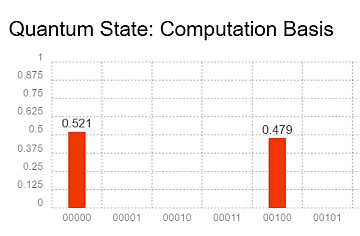
量子ビット2(5つ並んでいる数字の右から3番目)がもとの量子状態と同じく状態0と状態1が半々の重ね合わせの状態であることがわかるだろう。つまり重ね合わせ状態の転送に成功したことがわかるのだ。量子ビット0から量子ビット2へのほんのわずかな距離の量子テレポーテーションである。
5つの量子ビットが搭載されたIBMの量子コンピュータ心臓部

その他の感想、考えたこと
ファインマン先生は著書「ファインマン計算機科学:ファインマン, A.ヘイ, R.アレン」で量子コンピュータのアイデアを公表したが、それは原子サイズの素子を使ったコンピュータ、可逆計算ができるコンピュータという意味においてである。重ね合わせ状態を使った超超高速並列計算に関して言えばファインマン先生は気が付いていなかった。この点において量子コンピュータの本当の発案者はドイチェ・ジョザのアルゴリズムを考案者のうちのひとり、ドイチェである。
量子アルゴリズムの研究は始まったばかりだ。本書には「古典コンピュータのアルゴリズムのすべてが量子コンピュータで実現できるわけではない。」と書かれている。汎用量子コンピュータができるかどうかは原理的な問題なのか、研究を続ければ実現可能なのかは僕にはわからないが、後者であることを願いたい。「量子プログラミングの基礎: イン・ミンシェン」という本が出たばかりだが、現在のコンピュータのようにプログラミング言語を使って自在に開発を行えるような量子コンピュータが実現するのはもう少し先のようである。
量子アルゴリズムは本書を読みながらやっと理解できた。自分でアルゴリズムを考え量子ゲートを組み上げることはできないことを実感した。僕は古典コンピュータの論理ゲートを使ったデジタル回路さえ作ったことがないのだから、当然と言えば当然である。(参考記事:「電卓を作りたいという妄想」)
また、IBMの量子コンピュータで公開されているUser Guideだけ読んで量子アルゴリズムの実験をして遊ぶのも初心者には無理だ。専門書で学ぶか本書のような解説本を参照しながらであれば、高校生でも実験を楽しむことができる。ぜひ、ご自身で試してみてほしい。
ブログを始めて12年。現実の世界、ニューヨークに置かれた量子コンピュータを使って僕はようやく自分で量子テレポーテーションの実験を行なったことになる。小さいながらも今日は記念日だ。
著者の中山先生は次の本も2年前にお書きになっている。目次を見ると本書の理論的側面を学べる本だということがわかる。合わせてお読みになるとよいだろう。Kindle版は固定レイアウトなのでご注意。
「量子アルゴリズム:中山茂」(Kindle版)(目次)

量子コンピュータ関連の本: Amazonで検索
関連記事:
発売情報: クラウド量子計算入門: 中山茂
http://blog.goo.ne.jp/ktonegaw/e/d360b69100fbe723c5b9410dbf3f5f4d
量子コンピュータ入門:宮野健次郎、古澤明
http://blog.goo.ne.jp/ktonegaw/e/ef75709187cf4b35a12f2d9fdf73a320
ファインマン計算機科学:ファインマン, A.ヘイ, R.アレン
http://blog.goo.ne.jp/ktonegaw/e/4f7f453019fd463ed2bfdeaa7b288d79
量子コンピュータ、量子アルゴリズムを学びたい高校生のために
http://blog.goo.ne.jp/ktonegaw/e/1b2940b648bda682aa27192eb8261972
発売情報:量子プログラミングの基礎: イン・ミンシェン
http://blog.goo.ne.jp/ktonegaw/e/27e4d9a10982d4d69c0029fc4c801708
関連ページ:
IBMの量子コンピュータを使ってみた
http://kadora.hatenablog.com/entry/2016/09/10/230116
従来のPCの1億倍高速な量子コンピューターはどのような仕組みで動いて物理的限界を突破しているのかがわかるムービー
http://gigazine.net/news/20151210-quantum-computers-explained/
わかりやすい量子コンピュータ
http://matome.naver.jp/odai/2133630808407668301
「ITエンジニアのための量子コンピュータ入門」連載一覧
http://codezine.jp/article/corner/629
量子力学の反常識が創りだす量子コンピューティングの世界
~量子コンピュータの頭脳としての量子アルゴリズム~
http://www.kyoto-su.ac.jp/project/st/st14_03.html
米メリーランド大学、世界初となる「汎用計算可能量子コンピュータ」モジュールを開発
http://pc.watch.impress.co.jp/docs/news/1014034.html
関連動画:
量子論、量子テレポーテーション、量子コンピュータ
量子の制御とコンピュータ(量子コンピュータの原理の概要説明)
量子コンピュータ授業 #1(15回の講義。本書で解説される量子ゲート、量子アルゴリズムのほとんどを学ぶことができる。)
15回の講義内容

ブログ執筆のはげみになりますので、1つずつ応援クリックをお願いします。



とね日記は長年放置されている科学ブログランキングの不正クリックに対し、次のランキングサイトには適切な運営を期待します。
「FC2自然科学ブログランキング」:不正の例1 例2
「にほんブログ村、科学ブログランキング」:New-不正の例1
(不正クリックブログの見分け方)




「クラウド量子計算入門―IBMの量子シミュレーションと量子コンピュータ: 中山茂」

第1章 はじめてのIBMの5量子ビット実験
1.1 IBMの量子シミュレーションと量子コンピュータ実験
1.2 クラウド量子計算に期待されること
1.3 クラウド量子計算への歩み
1.4 はじめてのIBMのクラウド量子計算
1.5 はじめてのIBMの量子シミュレータ
1.6 はじめてのIBMの量子コンピュータ
第2章 パウリゲートの量子実験
2.1 パウリゲートとは
2.2 恒等ゲートとパウリゲートを使った量子シミュレータ実験
第3章 アダマールゲートの量子実験
3.1 アダマール変換とは
3.2 アダマール演算による量子シミュレータ実験
第4章 位相シフトゲートの量子実験
4.1 位相シフト演算とは
4.2 T深度による量子実験
第5章 制御NOTゲートの量子実験
5.1 制御NOTゲートと重ね合わせ状態
5.2 制御NOTゲートによるもつれ状態生成
5.3 制御NOTゲートにおけるパウリ演算子
5.4 制御NOTゲートによる交換ゲート
5.5 制御Uゲートの生成
第6章 トフォリゲートの量子実験
6.1 3量子ビットのもつれ状態
6.2 トフォリゲートの量子実験
6.3 フレッドキンゲートの量子実験
第7章 ドイチ・ジョザ問題の量子実験
7.1 ドイチ問題の量子実験
7.2 ドイチ・ジョザ問題の量子実験
第8章 ベルンシュタイン・ヴァジラニ問題の量子実験
8.1 関数f(x)=x・aの定数aを求めるベルンシュタイン・ヴァジラニ問題
8.2 n=1のベルンシュタイン・ヴァジラニ問題
8.3 n=2のベルンシュタイン・ヴァジラニ問題
8.4 n=3のベルンシュタイン・ヴァジラニ問題
第9章 サイモン問題の量子実験
9.1 サイモン問題とは
9.2 n=2のサイモン問題の量子実験
第10章 量子フーリエ変換の量子実験
10.1 量子フーリエ変換の定義
10.2 量子フーリエ変換に必要な制御Sゲートの作成
10.3 量子フーリエ変換ゲートの実装
10.4 逆量子フーリエ変換ゲート
10.5 量子フーリエ変換によるシフト不変性
第11章 位相・固有値・位数推定問題の量子実験
11.1 位相推定問題の量子実験
11.2 ユニタリ変換の固有値推定アルゴリズムの量子実験
11.3 位数発見アルゴリズムの量子実験
第12章 ショアの素因数分解問題の量子実験
12.1 因数分解とユークリッドの互除法
12.2 ショアの素因数分解アルゴリズム
12.3 ショアの素因数分解のための量子回路
第13章 グローバーの探索問題の量子実験
13.1 グローバーの探索問題とは
13.2 グローバーの振幅増幅手法の量子回路
第14章 量子非局所性の量子実験
14.1 量子非局所性とCHSH不等式
14.2 GHZ状態の量子非局所性実験
第15章 量子通信の量子実験
15.1 量子高密度符号
15.2 量子転送
第16章 量子エラーとスタビライザー測定
16.1 量子エラーとシンドローム診断
16.2 ビットパリティ識別
16.3 符号パリティ識別
第17章 量子誤り訂正の量子実験
17.1 量子誤り訂正のための符号化と複合化
17.2 量子誤り訂正ゲート