「開立はん」に1729.03を置いたところ拡大
今日のテーマは「ファインマン先生 v.s. 算盤の達人」である。
![]()
物理学者のリチャード・ファインマンは1949年に初めてブラジルを訪れた際に日本人の算盤の達人(算盤のセールスマン)と計算のスピードを競い合ったことがある。先生が31歳のときでこのエピソードは自伝の「ご冗談でしょう、ファインマンさん」の中の「ラッキー・ナンバー」という小話で紹介している。
加算、減算、乗算では算盤の達人に負けたが、複雑な除算では引き分け、立方根の問題ではファインマン先生が圧勝した。これは幸運にも立方根を求めるよう選ばれた数字が 1729.03 であり、1立方フィートが1728立方インチであることおよび誤差をどのように概算すべきかをファインマンが知っていたためだ。
Feynman vs. The Abacus
http://www.ee.ryerson.ca/~Elf/abacus/feynman.html
An Interesting Number (Feynman: 1729, 1729.03)
http://www.cut-the-knot.org/blue/InterestingStory.shtml
Feynman 氏の計算
http://www.math.u-ryukyu.ac.jp/~suga/ssh3/node6.html
この1729.03という数字は12の3乗の1728に近いため、ファインマン先生にかなり有利な例だ。小話のタイトルが「ラッキー・ナンバー」となっているのはそういう意味だ。
ファインマン先生やこの自伝本は大好きなのだが、このエピソードだけは好きになれなかった。日本人や算盤が馬鹿にされたということもあるし、他の数字を選んでいたらファインマン先生が負けていたのではないかと思えたからだ。結局この話の中で、日本人セールスマンは正解に至っていなかった。
算盤でこれを計算するのはどれくらい大変なのだろう?
負けてしまった日本人セールスマンの雪辱を68年ぶりに果たすことはできるのだろうか?
今回はこの1729.03の立方根を算盤で計算する手順の紹介である。本邦初公開!というよりネットを検索しても見当たらないから、おそらく世界初公開だと思う。
とはいっても、手順は第3回の記事で紹介した算盤の達人、青葉計算アカデミーを主宰している大関さんによるもので、僕は相変わらず他力本願である。教えていただいた計算手順を僕にも理解できるくらい詳しく書き直している。
この段階で読者のみなさんが理解できるとは思えない。この手順を理解することをこの連載記事の最終目標として、次回からはずっとやさしい「開平」の計算手順の解説を始める予定だ。
算盤による1729.03の3乗根の解法
さて計算手順を説明しよう。使っているのは3根法(3商法)と近似法だ。立方根計算専用の「開立はん」を購入したが、写真を撮るのが大変なのでExcel上に「バーチャル開立はん」を作ってスクリーンショットを撮ることにした。数字を入力すると珠が動くしくみになっている。(「せっかく買ったのに実物はいつ使うの?」という声が聞こえてくるが、無視させていただこう。)
フォーカスすべき桁は赤い文字にしておいた。最後のほうは近似計算を用いている。
![]()
手順1: 1729.03を置く。
![]()
手順2: Bに初根1を立てる。(1^3=1≦1)
![]()
手順3: Fの1から初根1を引く。
![]()
手順4: 729にフォーカスする。
![]()
手順5: 729を初根の3倍で割る。24余り9を置く。
![]()
手順6: Cに次根2を立てる。(2^3=8≦24)
![]()
手順7: EFの24から12x2を引く。
![]()
手順8: Iの9から次根2^3=8を引き、次根2を決定。
![]()
手順9: IJKLの1030にフォーカスする。
![]()
手順10: 1030を3x12で割る。
![]()
手順11: HIJKLの28611にフォーカスする。
![]()
手順12: そこまでの根、12で割る。第5根2をFに置く。(2^3=8≦28)
![]()
手順13: 28611から2x12002を引き、答4607を置く。
![]()
手順14: IJKLMNの460711にフォーカスする。
![]()
手順15: 460711を36(3x12)で掛け戻す。
![]()
手順16: 第5根2の3乗(=8)を引き、第5根を決定。つまり12.002時点で余りが0.165855992ということ。
![]()
手順17: 3x12002=36006で割る。
![]()
手順18: そこまでの根、12002で割る。第6根3を立て、3x120023を引く。
![]()
手順19: 余った100565を36006(3x12002)で掛け戻す。
![]()
手順20:第6根3の3乗(=27)を引き、第6根を決定。この時点での余り0.036209547833 3x120023=360069で割る。
![]()
手順21: この頃になると、誤差はほぼなくなっていると見込まれる。盤面の1005628000999800を、そこまでの根120023割り続ける。
![]()
手順22: 答12.002383786274
![]()
最終状態: 答12.002383786274(赤い文字のところまで正解と一致)
iPhoneを横向きにして表示される関数電卓で確認すると正確な数値は12.00238378569172である。算盤の結果は赤い文字の桁まで一致していることがわかる。最後の近似計算が小数点以下6桁から9桁までを計算するのに威力を発揮していることもわかる。
![]()
珠の状態変化を表にすると次のようになる。(クリックで拡大)
![]()
ファインマン先生がどれくらい時間をかけたのかはわからないが、この対決で小数点以下5桁の12.0023まで計算したそうだ。算盤だと手順18で小数点以下第5桁(第6根)の3を立てるが、決定されるのは手順20である。
たしかに1729.03はファインマン先生にとってラッキー・ナンバーだったのだ。でも他の数字だったとしたら算盤の達人が勝っていたことは想像にかたくない。
「ライウス、クビクス!」について
ところで、立方根対決を思いついたとき算盤の達人は「ライウス、クビクス!」と叫んだと「ご冗談でしょう、ファインマンさん」に書いてある。原書を見ると「Raios cubicos!」となっている。
ファイマン先生はブラジルでポルトガル語をマスターしたそうだが、どうも怪しい。ポルトガル語で立方根は「Raizes cúbicas(複数形)」で「ハイーセス・クビカス」と発音する。Raiosの単数形「Raio(発音はハイオ)」は光、線、半径、範囲などと訳され、球の体積「3分の4πr^3」を「4 pi raios cúbicos sobre 3」のように表記することもあるようだ。(「sobre」は「on」の意味。参考ページ。)
だから「Raios cubicos!」というのは「Cube radius!(立方半径!)」と言っているようなものなので、算盤の達人が間違えたのかファインマン先生が間違えたのかは判然としないのだが、明らかに「ライウス、クビクス!」は「立方根!」ではないのである。
第6回の記事は開平計算のしくみである。
関連記事:
武士の家計簿:磯田道史
http://blog.goo.ne.jp/ktonegaw/e/38e15f47cba2eaed5f1787c30b09eb7c
計算尺ノスタルジア (コンサイス計算尺、ヘンミ計算尺)
http://blog.goo.ne.jp/ktonegaw/e/b91ae7814c1830a9aaf7da77aadf88a8
アポロに搭載された計算尺(Pickett N600-ES)
http://blog.goo.ne.jp/ktonegaw/e/3898318d7f4b3e84900d9ae2cb80d816
機械式計算機ノスタルジア(タイガー計算器)
http://blog.goo.ne.jp/ktonegaw/e/226dd92e17d66ac624b7279776aa77f6
五桁ノ 對數表 及 三角函數表:えふ.げい.がうす著
http://blog.goo.ne.jp/ktonegaw/e/8d90de27b13365139c25bbffd9c4f04b
ブログ執筆のはげみになりますので、1つずつ応援クリックをお願いします。
![にほんブログ村 科学ブログ 物理学へ]()
![人気ブログランキングへ]()
![]()
とね日記は長年放置されている科学ブログランキングの不正クリックに対し、次のランキングサイトには適切な運営を期待します。
「FC2自然科学ブログランキング」:不正の例1 例2(クリックしてからTwitterアプリで開くと画像は鮮明に見れます。)
(不正クリックブログの見分け方)
![]()
![]()
![]()
![]()
今日のテーマは「ファインマン先生 v.s. 算盤の達人」である。

物理学者のリチャード・ファインマンは1949年に初めてブラジルを訪れた際に日本人の算盤の達人(算盤のセールスマン)と計算のスピードを競い合ったことがある。先生が31歳のときでこのエピソードは自伝の「ご冗談でしょう、ファインマンさん」の中の「ラッキー・ナンバー」という小話で紹介している。
加算、減算、乗算では算盤の達人に負けたが、複雑な除算では引き分け、立方根の問題ではファインマン先生が圧勝した。これは幸運にも立方根を求めるよう選ばれた数字が 1729.03 であり、1立方フィートが1728立方インチであることおよび誤差をどのように概算すべきかをファインマンが知っていたためだ。
Feynman vs. The Abacus
http://www.ee.ryerson.ca/~Elf/abacus/feynman.html
An Interesting Number (Feynman: 1729, 1729.03)
http://www.cut-the-knot.org/blue/InterestingStory.shtml
Feynman 氏の計算
http://www.math.u-ryukyu.ac.jp/~suga/ssh3/node6.html
この1729.03という数字は12の3乗の1728に近いため、ファインマン先生にかなり有利な例だ。小話のタイトルが「ラッキー・ナンバー」となっているのはそういう意味だ。
ファインマン先生やこの自伝本は大好きなのだが、このエピソードだけは好きになれなかった。日本人や算盤が馬鹿にされたということもあるし、他の数字を選んでいたらファインマン先生が負けていたのではないかと思えたからだ。結局この話の中で、日本人セールスマンは正解に至っていなかった。
算盤でこれを計算するのはどれくらい大変なのだろう?
負けてしまった日本人セールスマンの雪辱を68年ぶりに果たすことはできるのだろうか?
今回はこの1729.03の立方根を算盤で計算する手順の紹介である。本邦初公開!というよりネットを検索しても見当たらないから、おそらく世界初公開だと思う。
とはいっても、手順は第3回の記事で紹介した算盤の達人、青葉計算アカデミーを主宰している大関さんによるもので、僕は相変わらず他力本願である。教えていただいた計算手順を僕にも理解できるくらい詳しく書き直している。
この段階で読者のみなさんが理解できるとは思えない。この手順を理解することをこの連載記事の最終目標として、次回からはずっとやさしい「開平」の計算手順の解説を始める予定だ。
算盤による1729.03の3乗根の解法
さて計算手順を説明しよう。使っているのは3根法(3商法)と近似法だ。立方根計算専用の「開立はん」を購入したが、写真を撮るのが大変なのでExcel上に「バーチャル開立はん」を作ってスクリーンショットを撮ることにした。数字を入力すると珠が動くしくみになっている。(「せっかく買ったのに実物はいつ使うの?」という声が聞こえてくるが、無視させていただこう。)
フォーカスすべき桁は赤い文字にしておいた。最後のほうは近似計算を用いている。

手順1: 1729.03を置く。

手順2: Bに初根1を立てる。(1^3=1≦1)

手順3: Fの1から初根1を引く。

手順4: 729にフォーカスする。

手順5: 729を初根の3倍で割る。24余り9を置く。

手順6: Cに次根2を立てる。(2^3=8≦24)

手順7: EFの24から12x2を引く。

手順8: Iの9から次根2^3=8を引き、次根2を決定。

手順9: IJKLの1030にフォーカスする。

手順10: 1030を3x12で割る。

手順11: HIJKLの28611にフォーカスする。

手順12: そこまでの根、12で割る。第5根2をFに置く。(2^3=8≦28)

手順13: 28611から2x12002を引き、答4607を置く。

手順14: IJKLMNの460711にフォーカスする。

手順15: 460711を36(3x12)で掛け戻す。

手順16: 第5根2の3乗(=8)を引き、第5根を決定。つまり12.002時点で余りが0.165855992ということ。

手順17: 3x12002=36006で割る。
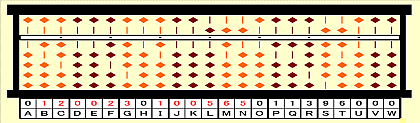
手順18: そこまでの根、12002で割る。第6根3を立て、3x120023を引く。

手順19: 余った100565を36006(3x12002)で掛け戻す。

手順20:第6根3の3乗(=27)を引き、第6根を決定。この時点での余り0.036209547833 3x120023=360069で割る。

手順21: この頃になると、誤差はほぼなくなっていると見込まれる。盤面の1005628000999800を、そこまでの根120023割り続ける。

手順22: 答12.002383786274

最終状態: 答12.002383786274(赤い文字のところまで正解と一致)
iPhoneを横向きにして表示される関数電卓で確認すると正確な数値は12.00238378569172である。算盤の結果は赤い文字の桁まで一致していることがわかる。最後の近似計算が小数点以下6桁から9桁までを計算するのに威力を発揮していることもわかる。

珠の状態変化を表にすると次のようになる。(クリックで拡大)

ファインマン先生がどれくらい時間をかけたのかはわからないが、この対決で小数点以下5桁の12.0023まで計算したそうだ。算盤だと手順18で小数点以下第5桁(第6根)の3を立てるが、決定されるのは手順20である。
たしかに1729.03はファインマン先生にとってラッキー・ナンバーだったのだ。でも他の数字だったとしたら算盤の達人が勝っていたことは想像にかたくない。
「ライウス、クビクス!」について
ところで、立方根対決を思いついたとき算盤の達人は「ライウス、クビクス!」と叫んだと「ご冗談でしょう、ファインマンさん」に書いてある。原書を見ると「Raios cubicos!」となっている。
ファイマン先生はブラジルでポルトガル語をマスターしたそうだが、どうも怪しい。ポルトガル語で立方根は「Raizes cúbicas(複数形)」で「ハイーセス・クビカス」と発音する。Raiosの単数形「Raio(発音はハイオ)」は光、線、半径、範囲などと訳され、球の体積「3分の4πr^3」を「4 pi raios cúbicos sobre 3」のように表記することもあるようだ。(「sobre」は「on」の意味。参考ページ。)
だから「Raios cubicos!」というのは「Cube radius!(立方半径!)」と言っているようなものなので、算盤の達人が間違えたのかファインマン先生が間違えたのかは判然としないのだが、明らかに「ライウス、クビクス!」は「立方根!」ではないのである。
第6回の記事は開平計算のしくみである。
関連記事:
武士の家計簿:磯田道史
http://blog.goo.ne.jp/ktonegaw/e/38e15f47cba2eaed5f1787c30b09eb7c
計算尺ノスタルジア (コンサイス計算尺、ヘンミ計算尺)
http://blog.goo.ne.jp/ktonegaw/e/b91ae7814c1830a9aaf7da77aadf88a8
アポロに搭載された計算尺(Pickett N600-ES)
http://blog.goo.ne.jp/ktonegaw/e/3898318d7f4b3e84900d9ae2cb80d816
機械式計算機ノスタルジア(タイガー計算器)
http://blog.goo.ne.jp/ktonegaw/e/226dd92e17d66ac624b7279776aa77f6
五桁ノ 對數表 及 三角函數表:えふ.げい.がうす著
http://blog.goo.ne.jp/ktonegaw/e/8d90de27b13365139c25bbffd9c4f04b
ブログ執筆のはげみになりますので、1つずつ応援クリックをお願いします。



とね日記は長年放置されている科学ブログランキングの不正クリックに対し、次のランキングサイトには適切な運営を期待します。
「FC2自然科学ブログランキング」:不正の例1 例2(クリックしてからTwitterアプリで開くと画像は鮮明に見れます。)
(不正クリックブログの見分け方)



