「低次元の幾何からポアンカレ予想へ : 市原一裕」(Kindle版)
内容紹介:
ビウスの帯、クラインの壺、オイラーの多面体定理、ポアンカレ予想など有名な幾何学をとりあげ、多様体の魅力に迫ります。
ポアンカレ予想は位相幾何学の予想の1つですが、きちんと理解しようとすると3次元の壁にぶつかり、あきらめてしまう人もいるようです。
本書では、身近な例を豊富に使って親近感がわくように説明します。多面体や次元がイメージできるようになるでしょう。
サーストンの幾何化予想にも言及します。
2018年1月刊行、208ページ。
著者について:
市原一裕(いちはら・かずひろ)
日本大学文理学部数学科教授。1972年生まれ。専攻は低次元位相幾何学、特に三次元多様体論、および数学教育学。主な著書『ひらいてわかる線形代数』(共著、数学書房、2011年)、教科書執筆『高等学校「数学」』(数研出版)、論文“Exceptional surgeries on alternating knots"など。
市原先生の著書: Amazonで検索
理数系書籍のレビュー記事は本書で369冊目。
2003年に証明された「ポアンカレ予想」が話題になったのは2007年に放送された「ハイビジョン特集 数学者はキノコ狩りの夢を見る ~ポアンカレ予想・100年の格闘~」や「NHKスペシャル 100年の難問はなぜ解けたのか ~天才数学者 失踪(しっそう)の謎~」がきっかけだ。
100年もの間、数学者たちを悩ませ続けた超難問だから一般人が証明を理解するのはもちろん不可能だ。どのような意味なのか、証明の流れを大まかにつかむだけでよいのなら話は違う。そのための教養書がいくつか刊行されていて、先日紹介した「数学ガール/ポアンカレ予想 : 結城浩」も、そのうちのひとつだ。
ポアンカレ予想を証明する鍵になったのが「サーストンの幾何化予想」と「ハミルトンのリッチ・フロー方程式」だ。「数学ガール/ポアンカレ予想」では最終章で24ページを割いて説明している。
今回紹介する「低次元の幾何からポアンカレ予想へ : 市原一裕」(Kindle版)は「サーストンの幾何化予想」と「ハミルトンのリッチ・フロー方程式」、「ペレルマンによるポアンカレ予想の証明」を数学者の市原先生が、より詳細かつ具体的、視覚的に解説をした本なのだ。数学の教養書の中ではかなり難しいほうだが、一般の読者でもなんとかついていくことができる。特に「サーストンの幾何化予想」の部分が全体の7割を占めており、一般読者に対してこれだけ詳しく解説した本は他にはないと思う。
とはいえ、論理的整合性を保ちつつすべてを説明し尽くすのは無理だったようだ。「この部分の説明は省略させていただきます。」とか「~のようなものだと思ってください。」のように説明を断念してしまっている箇所がかなり目につく。
それでも不満に思ったり、がっかりする必要はない。詳しく説明されている部分だけでもじゅうぶん難しく知的興奮が味わえるから、省略されても「ここまで説明してくれているのだから十分だ。」と思えてくるからだ。難しいところは次元を1つ下げて解説をしたりして、可能なかぎり具体的にたくさんのことを説明したいという先生のお気持が伝わってくる。
章立てはこのとおり。
巻頭 ポアンカレ予想に関わる図形たち
はじめに
第1章 ポアンカレ予想
第2章 多様体の幾何構造
第3章 サーストンの幾何化予想
第4章 ペレルマンの証明
付 録 非ユークリッド幾何について
読書案内
あとがき
第1章「ポアンカレ予想」では、次元や多様体、3次元球面、閉多様体、基本群の解説をしながらポアンカレ予想とはどういう意味なのかが明らかにされる。
第2章「多様体の幾何構造」ではまずサーストンの幾何化予想の意味が解説され、曲面や1次元の多様体を取り上げて「幾何化する」ということがどういうことなのかを理解することができる。幾何化できない多様体もあるのだ。次の図でKはガウス曲率。
![]()
第3章「サーストンの幾何化予想」が本書でいちばん難しく、そして重要だ。3次元多様体は無限にあるのに、断片は8種類に限られる。8つのの断片は、物理に例えれば原子、数に例えれば素数のような存在だ。なぜ8つに限られるのかが一般の人には不思議である。
![]()
この章では定曲率の幾何構造、直積幾何構造、ねじれ積の幾何構造を紹介し、最大で8つの幾何学しか考えられないことが解説される。これらの幾何学からサーストンが提示した幾何化予想がどのようなものなのか理解できるようになる。
たとえば直積幾何構造の説明では2次元トーラスと3次元トーラスは、このような図を使って説明されている。両側矢印で対応づけられる辺と辺、面と面は同一視して考える。
![]()
そして本書で紹介される直積幾何構造は、まず9種類求められ、そのうち1つが除外されることになる。(上の8つの断片の図と割当てられている英文字が違うが、図と表の英文字の対応関係はコメントとしてhirotaさんからいただいた説明を参照していただきたい。)
![]()
第4章「ペレルマンの証明」も読みごたえがある。リーマン計量やガウス曲率、リッチ曲率などを解説した後、ハミルトンが考案した「3次元多様体にリーマン計量を入れる」というアイデアが紹介される。リーマン計量を少しずつ変形していく過程で使われるのが「リッチ・フロー方程式」である。
巻頭にはホワイトヘッド絡み目、双曲正12面体、3次元球面のねじれ積(ホップ・ファイブレーション)、トーラス結び目、ザイフェエルト多様体、8の字結び目、リッチ・フローの様子などがカラーの美しいCGで紹介されている。
また、本文では次のような多様体や概念が紹介、解説されている。本書のレベルがおわかりになると思う。
ホワイトヘッド多様体、ポアンカレ12面体、レンズ空間、ザイフェルト・ウィーバー12面体、ファイバー束、ホップ・ファイブレーション、ザイフェルト多様体、デーン・ツイスト、Solv幾何学、サーストン幾何、サーストンの怪物定理、実質的ファイバリング予想、連結和分解、JSJ分解、トーラス分解定理、本質的トーラス、圧縮円盤、圧縮不可能曲面、8の字結び目、ハーケン多様体、デーンの補題、リーマン計量、リーマン多様体、ガウス曲率、曲率テンソル、リッチ曲率、リッチ・フロー方程式、アインシュタイン多様体、ハミルトンの定理、ネック・ピンチ、特異点、手術、単射半径、シガー・ソリトン、局所非崩壊定理、標準近傍定理、エントロピー、手術付きリッチ・フロー、有限時間消滅定理、グラフ多様体、アレクサンドロフ空間
ポアンカレ予想を証明したペレルマンが2002年と2003年に「リッチフローの三次元多様体への応用」として掲載した論文は一般公開されている。以下のアドレスをクリックするとPDFで読むことができる。(理解しろという意味で紹介したわけではない。)
http://arxiv.org/find/all/1/au:+Perelman_Grisha/0/1/0/all/0/1
ペレルマンによる論文ではないが「リッチフローによるポアンカレ予想と幾何化予想の完全な証明」も以下のPDFファイルで読める。(こちらは328ページもある)
http://www.ims.cuhk.edu.hk/~ajm/vol10/10_2.pdf
あわせて読みたい:
本書と非常に相性がよいのがこの本。PDFファイルが無料で公開されている。(紹介記事)
「3次元多様体入門(培風館) : 森元勘治」
![]()
専門書だと、あとこの2冊が良さそうだ。
「3次元リッチフローと幾何学的トポロジー: 戸田正人」
「リッチフローと幾何化予想:小林亮一」(書評)(他の購入先)
![]()
![]()
多様体の入門書、教科書は定番のものがいくつかあるが、昨年3月にはユニークな本が刊行された。この本もいずれ読んでみたい。
「具体例から学ぶ 多様体: 藤岡敦」
![]()
そして2007年に放送されたNHKの番組を書籍化したのがこの本。理数系が苦手な方でもたやすく読める教養書である。時間の制約から番組では放送されなかったことが、たくさん書かれている。
「NHKスペシャル 100年の難問はなぜ解けたのか 天才数学者の光と影 : 春日真人」(Kindle版)(文庫版)
![]()
関連記事:
数学ガール/ポアンカレ予想 : 結城浩
https://blog.goo.ne.jp/ktonegaw/e/769e2639898b351545e7ad8a8eba89d7
トポロジカル宇宙(完全版):根上生也著
https://blog.goo.ne.jp/ktonegaw/e/246a5c64c600c9c12c303231173ee9e2
無料公開:3次元多様体入門(培風館): 森元勘治
https://blog.goo.ne.jp/ktonegaw/e/7f5737d01d69c60f6320e28c049bc0f1
ブログ執筆のはげみになりますので、1つずつ応援クリックをお願いします。
![にほんブログ村 科学ブログ 物理学へ]()
![人気ブログランキングへ]()
![]()
![]()
![]()
![]()
![]()
「低次元の幾何からポアンカレ予想へ : 市原一裕」(Kindle版)
![]()
巻頭 ポアンカレ予想に関わる図形たち
はじめに
第1章 ポアンカレ予想
- 宇宙の形と3次元多様体
- 次元とは
- 多様体とは
- 3次元球面とは
- 閉多様体とは
- 基本群とは
第2章 多様体の幾何構造
- サーストンの幾何化予想とは
- 曲面の幾何化
- 1次元の幾何化
第3章 サーストンの幾何化予想
- 定曲率幾何構造
- ねじれ積の幾何構造
- 8つの幾何学
- 幾何化予想とは
- 幾何化予想からわかること
第4章 ペレルマンの証明
- リーマン計量
- 曲率とリッチ曲率
- ハミルトンとリッチ・フロー方程式
- ハミルトンの定理と残された問題
- ペレルマンが示したこと
付 録 非ユークリッド幾何について
- 球面幾何について
- 双曲幾何について
読書案内
あとがき
内容紹介:
ビウスの帯、クラインの壺、オイラーの多面体定理、ポアンカレ予想など有名な幾何学をとりあげ、多様体の魅力に迫ります。
ポアンカレ予想は位相幾何学の予想の1つですが、きちんと理解しようとすると3次元の壁にぶつかり、あきらめてしまう人もいるようです。
本書では、身近な例を豊富に使って親近感がわくように説明します。多面体や次元がイメージできるようになるでしょう。
サーストンの幾何化予想にも言及します。
2018年1月刊行、208ページ。
著者について:
市原一裕(いちはら・かずひろ)
日本大学文理学部数学科教授。1972年生まれ。専攻は低次元位相幾何学、特に三次元多様体論、および数学教育学。主な著書『ひらいてわかる線形代数』(共著、数学書房、2011年)、教科書執筆『高等学校「数学」』(数研出版)、論文“Exceptional surgeries on alternating knots"など。
市原先生の著書: Amazonで検索
理数系書籍のレビュー記事は本書で369冊目。
2003年に証明された「ポアンカレ予想」が話題になったのは2007年に放送された「ハイビジョン特集 数学者はキノコ狩りの夢を見る ~ポアンカレ予想・100年の格闘~」や「NHKスペシャル 100年の難問はなぜ解けたのか ~天才数学者 失踪(しっそう)の謎~」がきっかけだ。
100年もの間、数学者たちを悩ませ続けた超難問だから一般人が証明を理解するのはもちろん不可能だ。どのような意味なのか、証明の流れを大まかにつかむだけでよいのなら話は違う。そのための教養書がいくつか刊行されていて、先日紹介した「数学ガール/ポアンカレ予想 : 結城浩」も、そのうちのひとつだ。
ポアンカレ予想を証明する鍵になったのが「サーストンの幾何化予想」と「ハミルトンのリッチ・フロー方程式」だ。「数学ガール/ポアンカレ予想」では最終章で24ページを割いて説明している。
今回紹介する「低次元の幾何からポアンカレ予想へ : 市原一裕」(Kindle版)は「サーストンの幾何化予想」と「ハミルトンのリッチ・フロー方程式」、「ペレルマンによるポアンカレ予想の証明」を数学者の市原先生が、より詳細かつ具体的、視覚的に解説をした本なのだ。数学の教養書の中ではかなり難しいほうだが、一般の読者でもなんとかついていくことができる。特に「サーストンの幾何化予想」の部分が全体の7割を占めており、一般読者に対してこれだけ詳しく解説した本は他にはないと思う。
とはいえ、論理的整合性を保ちつつすべてを説明し尽くすのは無理だったようだ。「この部分の説明は省略させていただきます。」とか「~のようなものだと思ってください。」のように説明を断念してしまっている箇所がかなり目につく。
それでも不満に思ったり、がっかりする必要はない。詳しく説明されている部分だけでもじゅうぶん難しく知的興奮が味わえるから、省略されても「ここまで説明してくれているのだから十分だ。」と思えてくるからだ。難しいところは次元を1つ下げて解説をしたりして、可能なかぎり具体的にたくさんのことを説明したいという先生のお気持が伝わってくる。
章立てはこのとおり。
巻頭 ポアンカレ予想に関わる図形たち
はじめに
第1章 ポアンカレ予想
第2章 多様体の幾何構造
第3章 サーストンの幾何化予想
第4章 ペレルマンの証明
付 録 非ユークリッド幾何について
読書案内
あとがき
第1章「ポアンカレ予想」では、次元や多様体、3次元球面、閉多様体、基本群の解説をしながらポアンカレ予想とはどういう意味なのかが明らかにされる。
第2章「多様体の幾何構造」ではまずサーストンの幾何化予想の意味が解説され、曲面や1次元の多様体を取り上げて「幾何化する」ということがどういうことなのかを理解することができる。幾何化できない多様体もあるのだ。次の図でKはガウス曲率。

第3章「サーストンの幾何化予想」が本書でいちばん難しく、そして重要だ。3次元多様体は無限にあるのに、断片は8種類に限られる。8つのの断片は、物理に例えれば原子、数に例えれば素数のような存在だ。なぜ8つに限られるのかが一般の人には不思議である。
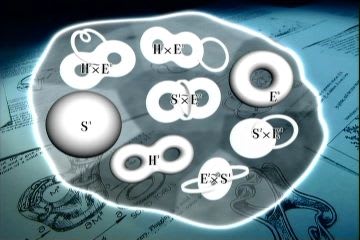
この章では定曲率の幾何構造、直積幾何構造、ねじれ積の幾何構造を紹介し、最大で8つの幾何学しか考えられないことが解説される。これらの幾何学からサーストンが提示した幾何化予想がどのようなものなのか理解できるようになる。
たとえば直積幾何構造の説明では2次元トーラスと3次元トーラスは、このような図を使って説明されている。両側矢印で対応づけられる辺と辺、面と面は同一視して考える。

そして本書で紹介される直積幾何構造は、まず9種類求められ、そのうち1つが除外されることになる。(上の8つの断片の図と割当てられている英文字が違うが、図と表の英文字の対応関係はコメントとしてhirotaさんからいただいた説明を参照していただきたい。)

第4章「ペレルマンの証明」も読みごたえがある。リーマン計量やガウス曲率、リッチ曲率などを解説した後、ハミルトンが考案した「3次元多様体にリーマン計量を入れる」というアイデアが紹介される。リーマン計量を少しずつ変形していく過程で使われるのが「リッチ・フロー方程式」である。
巻頭にはホワイトヘッド絡み目、双曲正12面体、3次元球面のねじれ積(ホップ・ファイブレーション)、トーラス結び目、ザイフェエルト多様体、8の字結び目、リッチ・フローの様子などがカラーの美しいCGで紹介されている。
また、本文では次のような多様体や概念が紹介、解説されている。本書のレベルがおわかりになると思う。
ホワイトヘッド多様体、ポアンカレ12面体、レンズ空間、ザイフェルト・ウィーバー12面体、ファイバー束、ホップ・ファイブレーション、ザイフェルト多様体、デーン・ツイスト、Solv幾何学、サーストン幾何、サーストンの怪物定理、実質的ファイバリング予想、連結和分解、JSJ分解、トーラス分解定理、本質的トーラス、圧縮円盤、圧縮不可能曲面、8の字結び目、ハーケン多様体、デーンの補題、リーマン計量、リーマン多様体、ガウス曲率、曲率テンソル、リッチ曲率、リッチ・フロー方程式、アインシュタイン多様体、ハミルトンの定理、ネック・ピンチ、特異点、手術、単射半径、シガー・ソリトン、局所非崩壊定理、標準近傍定理、エントロピー、手術付きリッチ・フロー、有限時間消滅定理、グラフ多様体、アレクサンドロフ空間
ポアンカレ予想を証明したペレルマンが2002年と2003年に「リッチフローの三次元多様体への応用」として掲載した論文は一般公開されている。以下のアドレスをクリックするとPDFで読むことができる。(理解しろという意味で紹介したわけではない。)
http://arxiv.org/find/all/1/au:+Perelman_Grisha/0/1/0/all/0/1
ペレルマンによる論文ではないが「リッチフローによるポアンカレ予想と幾何化予想の完全な証明」も以下のPDFファイルで読める。(こちらは328ページもある)
http://www.ims.cuhk.edu.hk/~ajm/vol10/10_2.pdf
あわせて読みたい:
本書と非常に相性がよいのがこの本。PDFファイルが無料で公開されている。(紹介記事)
「3次元多様体入門(培風館) : 森元勘治」

専門書だと、あとこの2冊が良さそうだ。
「3次元リッチフローと幾何学的トポロジー: 戸田正人」
「リッチフローと幾何化予想:小林亮一」(書評)(他の購入先)


多様体の入門書、教科書は定番のものがいくつかあるが、昨年3月にはユニークな本が刊行された。この本もいずれ読んでみたい。
「具体例から学ぶ 多様体: 藤岡敦」

そして2007年に放送されたNHKの番組を書籍化したのがこの本。理数系が苦手な方でもたやすく読める教養書である。時間の制約から番組では放送されなかったことが、たくさん書かれている。
「NHKスペシャル 100年の難問はなぜ解けたのか 天才数学者の光と影 : 春日真人」(Kindle版)(文庫版)

関連記事:
数学ガール/ポアンカレ予想 : 結城浩
https://blog.goo.ne.jp/ktonegaw/e/769e2639898b351545e7ad8a8eba89d7
トポロジカル宇宙(完全版):根上生也著
https://blog.goo.ne.jp/ktonegaw/e/246a5c64c600c9c12c303231173ee9e2
無料公開:3次元多様体入門(培風館): 森元勘治
https://blog.goo.ne.jp/ktonegaw/e/7f5737d01d69c60f6320e28c049bc0f1
ブログ執筆のはげみになりますので、1つずつ応援クリックをお願いします。







「低次元の幾何からポアンカレ予想へ : 市原一裕」(Kindle版)

巻頭 ポアンカレ予想に関わる図形たち
はじめに
第1章 ポアンカレ予想
- 宇宙の形と3次元多様体
- 次元とは
- 多様体とは
- 3次元球面とは
- 閉多様体とは
- 基本群とは
第2章 多様体の幾何構造
- サーストンの幾何化予想とは
- 曲面の幾何化
- 1次元の幾何化
第3章 サーストンの幾何化予想
- 定曲率幾何構造
- ねじれ積の幾何構造
- 8つの幾何学
- 幾何化予想とは
- 幾何化予想からわかること
第4章 ペレルマンの証明
- リーマン計量
- 曲率とリッチ曲率
- ハミルトンとリッチ・フロー方程式
- ハミルトンの定理と残された問題
- ペレルマンが示したこと
付 録 非ユークリッド幾何について
- 球面幾何について
- 双曲幾何について
読書案内
あとがき