開平と開立（第34回）：54,756の算盤による開平（半九九法4）

「開平はん」に54,756を置いたところ拡大

[English]

前回に続き、算盤での開平の手順を解説する。今回も半九九法で、根が３桁になる場合の基本編。理論編も参考にしていただきたい。全体の目次はこのページを開くと見ることができる。

開平（平方根）：倍根法(2商法)、倍根法別法、半九九法、半九九法別法、乗減法、定数法(折衷法) 、過大数開平、省略開平など


算盤による54,756の2乗根の解法（答は234）

第１群の数とは平方根を求める数を２桁ずつ区切り、いちばん大きい（いちばん左）の２桁のことである。群の数が根の桁数となる。

54,756 -> (05|47|56) : 5が第１群の数、根の桁数は3


手順1: 54756をDEFGHに置く。


手順2: 第1群は05。


手順3: 5以下の平方数は4=2x2。2を初根としてBに立てる。


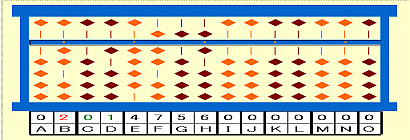
手順4: 5-2^2=01をCDに置く。


手順5: DEFGHの14756に注目する。


手順6: 14756を二分する。すなわち14756/2=07378をDEFGHに置く。


手順7: Eの7を既根2で割る。


手順8: 7/2=3余り1。商3をCに置き、次根とする。


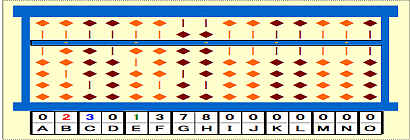
手順9: 余り1をEに置く。


手順10: EFGの137に注目する。


手順11: EFGの137から次根^2/2を引く。137-3^2/2=092をEFGに置く。


手順12: FGの92を既根23で割る。92/23=4余り0


手順13: 商4を得てDに置き、第3根とする。


手順14: 余り00をFGに置く。


手順15: Hの8に注目する。


手順16: Hの8から第3根^2/2を引く。8-4^2/2=0をHに置く。


手順17: 平方根は234と求まる。


最終状態： 答 234

珠の状態推移を表にすると次のようになる。（クリックで拡大）


同じ問題の倍根法での解法と比べてみてほしい。

次回も半九九法による開平だが、もう少し難しい例をとりあげる。


関連記事：

ファインマン v.s. 算盤の達人： ファインマン先生に立方根計算の雪辱を果たそう
http://blog.goo.ne.jp/ktonegaw/e/89a0b907577f03ef6132cf9664bdcddb

目次：算盤による平方根、立方根の計算（開平、開立）
http://blog.goo.ne.jp/ktonegaw/e/bb0449f357398a2c24026f33af7f70ee

開平と開立（第11回）：54,756の算盤による開平（倍根法５）
http://blog.goo.ne.jp/ktonegaw/e/c343dbd80ed9d66c7978e2fae18443da


ブログ執筆のはげみになりますので、１つずつ応援クリックをお願いします。
　　

「にほんブログ村」では、「科学ブログ 人気ランキング」と「注目記事ランキング（科学）」をくらべることでランキングを不正な手段を使って上げているブログがすぐわかるように作られている。不正行為はこのページのいちばん下に設置されたフォームから通報できる。（不正クリックの例）