[Set 12,895,213,625 on Mr. Cube root]Zoom
[Japanese]
Today's example is also about actual solution of Cube root using abacus. The calculation becomes more complicated than previous example.
Today's example is simple - basic Triple-root method, root is 4-digits case. Please check the Theory page for your reference.
Cube root methods: Triple-root method, constant number method, 3a^2 method, 1/3-division method, 1/3-multiplication table method, 1/3-multiplication table alternative method, Multiplication-Subtraction method, 3-root^2 method, Mixing method, Exceed number method, Omission Method, etc.
Abacus steps to solve Cube root of 12,895,213,625
(Answer is 2,345)
"1st group number" is the left most numbers in the 3-digits groups of the given number for cube root calculation. Number of groups is the number of digits of the Cube root.
12,895,213,625 -> (12|895|213|625): 12 is the 1st group number. The root digits is 4.
![]()
Step 1: Set 12895213625. First group is 12.
![]()
Step 2: Cube number smaller than 12 is 8=2^3. Place 2 on E as 1st root.
![]()
Step 3: Place 12-8=04 on HI. ( -a^3)
![]()
Step 4: Place Triple root 3x2=6 on B.
![]()
Step 5: Repeat division by triple root 6 until 4th digits next to 1st root. ( /3a)
![]()
Step 6: 48/6=8 remainder 0. Place 8 on G.
![]()
Step 7: Place remainder 00 on IJ.
![]()
Step 8: 9/6=1 remainder 3.
![]()
Step 9: Place 1 on I.
![]()
Step 10: Place remainder 3 on K.
![]()
Step 11: Divide 0 on F by current root 2.
![]()
Step 12: Get 3 as 2nd root and place it on F.
![]()
Step 13: Place 8-2x3=2 on H.
![]()
Step 14: Subtract 2nd root^2 from 21 on HI. ( -b^2)
![]()
Step 15: Place 21-3^2=12 on HI.
![]()
Step 16: Multiply triple root 6 by remainder 12 on HI. 6X12=72
![]()
Step 17: Replace 12 by 00 on HI.
![]()
Step 18: Add 72 to 03 on JK.
![]()
Step 19: It means place 03+72=75 on JK.
![]()
Step 20: Subtract 2nd root^3 from 755 on JKL. ( -b^3)
![]()
Step 21: It means place 755-3^3=728 on JKL.
![]()
Step 22: Add 3x2nd root to triple root on BC.
![]()
Step 23: Place 60+3x3=69 on BC.
![]()
Step 24: Repeat division by triple root 69 until fixed position.
![]()
Step 25: 72/69=1 remainder 3. Place 1 on H.
![]()
Step 26: Place remainder 03 on JK.
![]()
Step 27: 38/69=0 remainder 38
![]()
Step 28: Place 0 on I. Place remainder 38 on KL.
![]()
Step 29: 382/69=5 remainder 37
![]()
Step 30: Place 5 on J.
![]()
Step 31: Place remainder 037 on JKL.
![]()
Step 32: 371/69=5 remainder 26
![]()
Step 33: Place 5 on K.
![]()
Step 34: Place remainder 026 on LMN.
![]()
Step 35: Divide 105 on HIJ by current root 23. 105/23=4 remainder 13
![]()
Step 36: Place 4 on G as 3rd root.
![]()
Step 37: Place remainder 013 on HIJ.
![]()
Step 38: Subtract 3rd root^2 from 135 on IJK. ( -c^2)
![]()
Step 39: Place 135-4^2=119 on IJK.
![]()
Step 40: Multiply triple root 69 by remainder 119 on IJK. 69X119=8211
![]()
Step 41: Replace 119 by 000 on IJK.
![]()
Step 42: Add 8211 to 0026 on KLMN.
![]()
Step 43: It means place 0026+8211=8237 on KLMN.
![]()
Step 44: Subtract 3rd root^3 from 73 on NO. ( -c^3)
![]()
Step 45: Place 73-4^3=09 onNO.
![]()
Step 46: Add 3x3rd root to triple root on BCD.
![]()
Step 47: Place 690+3x4=702 on BCD.
![]()
Step 48: Repeat division by triple root 702 until fixed position.
![]()
Step 49: 823/702=1 remainder 121. Place 1 on I.
![]()
Step 50: Place remainder 121 on KLM.
![]()
Step 51: 1210/702=1 remainder 508
![]()
Step 52: Place 1 on J.
![]()
Step 53: Place remainder 0508 on KLMN.
![]()
Step 54: 5089/702=7 remainder 175
![]()
Step 55: Place 7 on K.
![]()
Step 56: Place remainder 0175 on LMNO.
![]()
Step 57: 1756/702=2 remainder 352
![]()
Step 58: Place 2 on L.
![]()
Step 59: Place remainder 0352 on MNOP.
![]()
Step 60: 3522/702=5 remainder 12
![]()
Step 61: Place 5 on M.
![]()
Step 62: Place remainder 0012 on NOPQ.
![]()
Step 63: Divide 1172 on JKLM by current root 234. 1172/234=5 remainder 2
![]()
Step 64: Place 5 on G as 4th root.
![]()
Step 65: Place remainder 0002 on IJKL.
![]()
Step 66: Subtract 4th root^2 from 25 on LM. ( -d^2)
![]()
Step 67: Place 25-5^2=00 on LM.
![]()
Step 68: Subtract 4th root^3 from 125 on PQR. (-d^2)
![]()
Step 69: Place 125-5^3=000 on PQR.
![]()
Step 70: Cube root of 12895213625 is 2345.
![]()
Final state: Answer 2345
Abacus state transition. (Click to Zoom)
![]()
![]()
![]()
Related articles:
How to solve Cube root of 1729.03 using abacus? (Feynman v.s. Abacus man)
http://blog.goo.ne.jp/ktonegaw/e/cff5d6e7ecaa07230b9cc7af10b23aed
Index: Square root and Cube root using Abacus
http://blog.goo.ne.jp/ktonegaw/e/f62fb31b6a3a0417ec5d33591249451b
Please place your mouse on the buttons and click one by one. These are blog ranking sites.
![にほんブログ村 科学ブログ 物理学へ]()
![人気ブログランキングへ]()
![]()
[Japanese]
Today's example is also about actual solution of Cube root using abacus. The calculation becomes more complicated than previous example.
Today's example is simple - basic Triple-root method, root is 4-digits case. Please check the Theory page for your reference.
Cube root methods: Triple-root method, constant number method, 3a^2 method, 1/3-division method, 1/3-multiplication table method, 1/3-multiplication table alternative method, Multiplication-Subtraction method, 3-root^2 method, Mixing method, Exceed number method, Omission Method, etc.
Abacus steps to solve Cube root of 12,895,213,625
(Answer is 2,345)
"1st group number" is the left most numbers in the 3-digits groups of the given number for cube root calculation. Number of groups is the number of digits of the Cube root.
12,895,213,625 -> (12|895|213|625): 12 is the 1st group number. The root digits is 4.

Step 1: Set 12895213625. First group is 12.

Step 2: Cube number smaller than 12 is 8=2^3. Place 2 on E as 1st root.

Step 3: Place 12-8=04 on HI. ( -a^3)

Step 4: Place Triple root 3x2=6 on B.

Step 5: Repeat division by triple root 6 until 4th digits next to 1st root. ( /3a)

Step 6: 48/6=8 remainder 0. Place 8 on G.

Step 7: Place remainder 00 on IJ.

Step 8: 9/6=1 remainder 3.

Step 9: Place 1 on I.

Step 10: Place remainder 3 on K.

Step 11: Divide 0 on F by current root 2.

Step 12: Get 3 as 2nd root and place it on F.

Step 13: Place 8-2x3=2 on H.
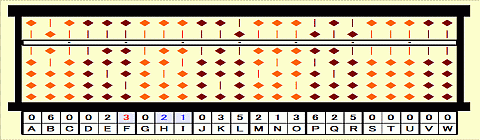
Step 14: Subtract 2nd root^2 from 21 on HI. ( -b^2)

Step 15: Place 21-3^2=12 on HI.

Step 16: Multiply triple root 6 by remainder 12 on HI. 6X12=72

Step 17: Replace 12 by 00 on HI.

Step 18: Add 72 to 03 on JK.

Step 19: It means place 03+72=75 on JK.

Step 20: Subtract 2nd root^3 from 755 on JKL. ( -b^3)

Step 21: It means place 755-3^3=728 on JKL.

Step 22: Add 3x2nd root to triple root on BC.

Step 23: Place 60+3x3=69 on BC.

Step 24: Repeat division by triple root 69 until fixed position.

Step 25: 72/69=1 remainder 3. Place 1 on H.

Step 26: Place remainder 03 on JK.

Step 27: 38/69=0 remainder 38

Step 28: Place 0 on I. Place remainder 38 on KL.

Step 29: 382/69=5 remainder 37

Step 30: Place 5 on J.

Step 31: Place remainder 037 on JKL.

Step 32: 371/69=5 remainder 26

Step 33: Place 5 on K.

Step 34: Place remainder 026 on LMN.

Step 35: Divide 105 on HIJ by current root 23. 105/23=4 remainder 13

Step 36: Place 4 on G as 3rd root.

Step 37: Place remainder 013 on HIJ.

Step 38: Subtract 3rd root^2 from 135 on IJK. ( -c^2)

Step 39: Place 135-4^2=119 on IJK.

Step 40: Multiply triple root 69 by remainder 119 on IJK. 69X119=8211

Step 41: Replace 119 by 000 on IJK.

Step 42: Add 8211 to 0026 on KLMN.

Step 43: It means place 0026+8211=8237 on KLMN.

Step 44: Subtract 3rd root^3 from 73 on NO. ( -c^3)

Step 45: Place 73-4^3=09 onNO.

Step 46: Add 3x3rd root to triple root on BCD.
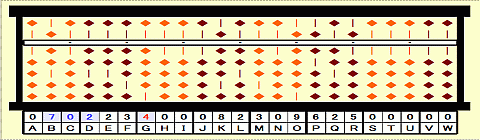
Step 47: Place 690+3x4=702 on BCD.

Step 48: Repeat division by triple root 702 until fixed position.

Step 49: 823/702=1 remainder 121. Place 1 on I.

Step 50: Place remainder 121 on KLM.

Step 51: 1210/702=1 remainder 508

Step 52: Place 1 on J.

Step 53: Place remainder 0508 on KLMN.

Step 54: 5089/702=7 remainder 175

Step 55: Place 7 on K.

Step 56: Place remainder 0175 on LMNO.

Step 57: 1756/702=2 remainder 352
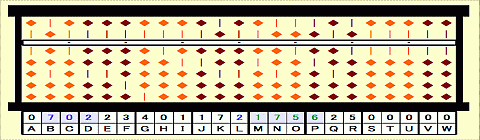
Step 58: Place 2 on L.

Step 59: Place remainder 0352 on MNOP.

Step 60: 3522/702=5 remainder 12

Step 61: Place 5 on M.

Step 62: Place remainder 0012 on NOPQ.

Step 63: Divide 1172 on JKLM by current root 234. 1172/234=5 remainder 2
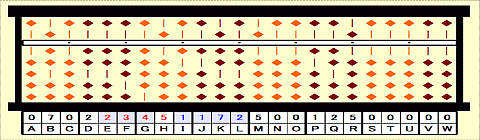
Step 64: Place 5 on G as 4th root.

Step 65: Place remainder 0002 on IJKL.

Step 66: Subtract 4th root^2 from 25 on LM. ( -d^2)

Step 67: Place 25-5^2=00 on LM.

Step 68: Subtract 4th root^3 from 125 on PQR. (-d^2)

Step 69: Place 125-5^3=000 on PQR.

Step 70: Cube root of 12895213625 is 2345.

Final state: Answer 2345
Abacus state transition. (Click to Zoom)



Related articles:
How to solve Cube root of 1729.03 using abacus? (Feynman v.s. Abacus man)
http://blog.goo.ne.jp/ktonegaw/e/cff5d6e7ecaa07230b9cc7af10b23aed
Index: Square root and Cube root using Abacus
http://blog.goo.ne.jp/ktonegaw/e/f62fb31b6a3a0417ec5d33591249451b
Please place your mouse on the buttons and click one by one. These are blog ranking sites.




















