[Set 421,875 on Mr. Cube root]Zoom
[Japanese]
We start the actual solutions to calculate Cube root using abacus. The calculation becomes more complicated but interesting.
Today's example is simple - basic Triple-root method, root is 2-digits case and 1st root is greater than or equal to 4.. Please check the Theory page for your reference.
Cube root methods: Triple-root method, constant number method, 3a^2 method, 1/3-division method, 1/3-multiplication table method, 1/3-multiplication table alternative method, Multiplication-Subtraction method, 3-root^2 method, Mixing method, Exceed number method, Omission Method, etc.
Abacus steps to solve Square root of 421,875
(Answer is 75)
"1st group number" is the left most numbers in the 3-digits groups of the given number for cube root calculation. Number of groups is the number of digits of the Cube root.
421,875 -> (421|875) : 421 is the 1st group number. The root digits is 2.
Image may be NSFW.
Clik here to view.
Step 1: Set 421875. First group is 421.
Image may be NSFW.
Clik here to view.
Step 2: Cube number smaller than 421 is 343=7^3. Place 7 on D as 1st root.
Image may be NSFW.
Clik here to view.
Step 3: Place 421-343=078 on GHI. (-a^3)
Image may be NSFW.
Clik here to view.
Step 4: Place Triple root 3x7=21 on AB.
Image may be NSFW.
Clik here to view.
Step 5: Repeat division by 21 until 4th digits next to 1st root. (/3a)
Image may be NSFW.
Clik here to view.
Step 6: 78/21=3 remainder 15. Place 3 on F and 15 on HI.
Image may be NSFW.
Clik here to view.
Step 7: Divide 158 by 21.
Image may be NSFW.
Clik here to view.
Step 8: 158/21=7 remainder 11. Place 7 on G and 011 on HIJ.
Image may be NSFW.
Clik here to view.
Step 9: Divide 117 by 21.
Image may be NSFW.
Clik here to view.
Step 10: 117/21=5 remainder 12 Place 5 on H and 012 on IJK.
Image may be NSFW.
Clik here to view.
Step 11: Divide 37 by current root (1st root) 7. (/a)
Image may be NSFW.
Clik here to view.
Step 12: Ansewer is 5 and place 5 on E as 2nd root.
Image may be NSFW.
Clik here to view.
Step 13: Place 37-1st root x Answer=37-7x5=02 on FG. (-ab)
Image may be NSFW.
Clik here to view.
Step 14: Focus on 25 on GH.
Image may be NSFW.
Clik here to view.
Step 15: Place 25-2nd root^2=25-5^2=00 on GH. (-b^2)
Image may be NSFW.
Clik here to view.
Step 16: Focus on 125 on JKL.
Image may be NSFW.
Clik here to view.
Step 17: Place 125-2nd root^2=125-5^3=000 on JKL. (-b^3)
Image may be NSFW.
Clik here to view.![]()
Step 18: Cube root is 75.
Image may be NSFW.
Clik here to view.![]()
Final state: Answer 75
Abacus state transition. (Click to Zoom)
Image may be NSFW.
Clik here to view.![]()
Next article is also about Cube root calculation (Triple-root method).
Related articles:
How to solve Cube root of 1729.03 using abacus? (Feynman v.s. Abacus man)
http://blog.goo.ne.jp/ktonegaw/e/cff5d6e7ecaa07230b9cc7af10b23aed
Please place your mouse on the buttons and click one by one. These are blog ranking sites.
Image may be NSFW.
Clik here to view.![にほんブログ村 科学ブログ 物理学へ]() Image may be NSFW.
Image may be NSFW.
Clik here to view.![人気ブログランキングへ]() Image may be NSFW.
Image may be NSFW.
Clik here to view.![]()
[Japanese]
We start the actual solutions to calculate Cube root using abacus. The calculation becomes more complicated but interesting.
Today's example is simple - basic Triple-root method, root is 2-digits case and 1st root is greater than or equal to 4.. Please check the Theory page for your reference.
Cube root methods: Triple-root method, constant number method, 3a^2 method, 1/3-division method, 1/3-multiplication table method, 1/3-multiplication table alternative method, Multiplication-Subtraction method, 3-root^2 method, Mixing method, Exceed number method, Omission Method, etc.
Abacus steps to solve Square root of 421,875
(Answer is 75)
"1st group number" is the left most numbers in the 3-digits groups of the given number for cube root calculation. Number of groups is the number of digits of the Cube root.
421,875 -> (421|875) : 421 is the 1st group number. The root digits is 2.
Image may be NSFW.
Clik here to view.

Step 1: Set 421875. First group is 421.
Image may be NSFW.
Clik here to view.

Step 2: Cube number smaller than 421 is 343=7^3. Place 7 on D as 1st root.
Image may be NSFW.
Clik here to view.

Step 3: Place 421-343=078 on GHI. (-a^3)
Image may be NSFW.
Clik here to view.

Step 4: Place Triple root 3x7=21 on AB.
Image may be NSFW.
Clik here to view.

Step 5: Repeat division by 21 until 4th digits next to 1st root. (/3a)
Image may be NSFW.
Clik here to view.

Step 6: 78/21=3 remainder 15. Place 3 on F and 15 on HI.
Image may be NSFW.
Clik here to view.

Step 7: Divide 158 by 21.
Image may be NSFW.
Clik here to view.

Step 8: 158/21=7 remainder 11. Place 7 on G and 011 on HIJ.
Image may be NSFW.
Clik here to view.

Step 9: Divide 117 by 21.
Image may be NSFW.
Clik here to view.

Step 10: 117/21=5 remainder 12 Place 5 on H and 012 on IJK.
Image may be NSFW.
Clik here to view.

Step 11: Divide 37 by current root (1st root) 7. (/a)
Image may be NSFW.
Clik here to view.

Step 12: Ansewer is 5 and place 5 on E as 2nd root.
Image may be NSFW.
Clik here to view.

Step 13: Place 37-1st root x Answer=37-7x5=02 on FG. (-ab)
Image may be NSFW.
Clik here to view.
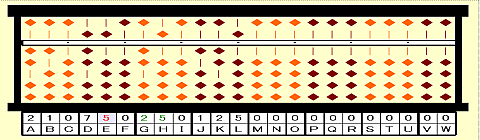
Step 14: Focus on 25 on GH.
Image may be NSFW.
Clik here to view.

Step 15: Place 25-2nd root^2=25-5^2=00 on GH. (-b^2)
Image may be NSFW.
Clik here to view.

Step 16: Focus on 125 on JKL.
Image may be NSFW.
Clik here to view.

Step 17: Place 125-2nd root^2=125-5^3=000 on JKL. (-b^3)
Image may be NSFW.
Clik here to view.

Step 18: Cube root is 75.
Image may be NSFW.
Clik here to view.

Final state: Answer 75
Abacus state transition. (Click to Zoom)
Image may be NSFW.
Clik here to view.

Next article is also about Cube root calculation (Triple-root method).
Related articles:
How to solve Cube root of 1729.03 using abacus? (Feynman v.s. Abacus man)
http://blog.goo.ne.jp/ktonegaw/e/cff5d6e7ecaa07230b9cc7af10b23aed
Please place your mouse on the buttons and click one by one. These are blog ranking sites.
Image may be NSFW.
Clik here to view.
 Image may be NSFW.
Image may be NSFW.Clik here to view.
 Image may be NSFW.
Image may be NSFW.Clik here to view.
