「ゴム弾性(初版復刻版):久保亮五」
内容紹介:
本書の初版は1947年に刊行され、その後絶版となりましたが、発刊翌年に毎日出版文化賞を受賞し、著者が若くして表された、現在でも学問的にきわめて価値の高い幻の名著として今日まで語り継がれてまいりました。
著者は1995年3月に亡くなられましたが、著者の業績を忍ぶ各方面から復刊の要望が高く、読みやすい現代版として復刻したものです。
ゴムの物理や化学は今日でもなお未解決の問題も多く、当時少壮気鋭の学者としてこの問題に取り組まれた著者の、ゴム弾性の神秘をあばこうとして構想をめぐらす姿勢がうかがわれる本書は、直接この方面に携わる方々を魅了するばかりでなく、多くの方々の興奮を呼び起こすことでありましょう。復刻版は1996年6月刊行、176ページ。
著者について:
久保亮五(くぼりょうご):ウィキペディアの記事
1920年 東京に生まれる。東京大学教授、京都大学教授、慶應大学教授、日本物理学会会長などを歴任。東京大学名誉教授、理学博士。統計物理学、物性物理学の分野で国際的に知られた。 特に線形応答理論の構築に貢献し、彼の提案した理論は「久保理論」の名でも呼ばれている。 1997年に生前の業績を記念して井上科学振興財団が久保亮五記念賞を創設した。
久保先生の著書、訳書: Amazonで検索する
理数系書籍のレビュー記事は本書で285冊目。
小学校ではバネにおもりを吊るす実験をして張力とバネの伸びが比例するという「フックの法則」を学ぶ。僕はこの実験をしたとき、バネではなくてゴムを使っても同じになるのかなと思って試してみたことがある。輪ゴムをいくつもつないでバネのかわりにして、おもりのかわりに10円玉を何枚も使って実験した。
その当時、八百屋さんでは「ばね秤」が使われていたけれども、子供たちの身の回りにあってすぐ手に入るのは輪ゴムや女の子たちが「ゴム段」で遊ぶために使っていた長いゴムの輪だった。どちらも日常的に目にしていたものだから、僕がゴムを使って秤を作ってみたらと思いついたのは自然なことだ。
実験の記録はノートに書かなかったので詳しいことは忘れてしまったが、伸びの長さと張力が比例していなかったことだけは覚えている。なぜなのだろう?と先生に聞いてみたことも覚えているが、当時教えていただいた先生は理数系の大学で学んでいない若い女の先生だったので、今になって思うと先生に答えられたはずがない。
結果がどうなるのか、ネットで調べてみたところ次のようになることがわかった。
点線は初めて引っ張ったときの伸びと張力の関係、実線は10回ほどゴムを伸ばしたり元に戻したりした後に測定した伸びと張力の関係である。
![]()
輪ゴムで身近なものの質量を量る
http://www.ons.ne.jp/~taka1997/education/2012/1-physics/14/
注意:このページではフックの法則を無理矢理あてはめてグラフを直線化させてしまっているが、測定値を見る限りフックの法則は成り立っていないと僕は思う。もちろんどんな曲線であっても部分的には直線に近似できるわけだが。物理は初めに法則ありきではない。現実の結果を最優先すべきである。縦と横の軸がこのブログ記事のグラフと逆になっていることにも注意。
けれども僕にできることはそこまでで、それ以来、現在に至るまでゴムがなぜ「フックの法則」に従わないのか、どのようなしくみで伸びるのかは謎のままだった。そしてこの10年ほど物理学を学んできたが、この話題に触れている本はひとつもなかった。ゴムについて僕はほとんど何も知らない。僕にとってゴムは知識の平原の中にぽっかり空いている「無知の穴」のようなものだ。
要素還元主義を無理矢理こじつければ、ゴムの弾性は4つの力のうち電磁気力によるものだろうけれど、それでは安直すぎる。ファンデルワールス力(分子間力)も関係していそうだし。(実際、条件によっては関係しているのだ。)
その後、ゴムは繊維状の高分子の集合体であり、ほつれた毛糸の塊を伸ばすようなイメージで伸びるのだと感覚的にとらえるようになったが、これも定性的な理解をしているに過ぎないわけで。。。
相対性理論や量子力学、素粒子物理学などの基礎物理学も大事だけど、身の回りの物のしくみも知っておくのも大切だから今年は物性物理を学び始めている。ゴムのしくみは高分子物性物理だ。
本書はこのテーマについて統計物理学、物性物理学の大家でいらっしゃる久保亮五先生が27歳のときに研究成果をまとめて出版された本である。初版が刊行されたのは1947年で、1996年に復刻版として刊行された名著だ。久保先生の処女作でもある。
ゴムの弾性について定性的な理解が深まるだけでなく、いくつかの物理モデルに従った理論にもとづいた定式化により、定量的な理解も深めることができる。前提知識として熱力学、統計力学が必要になる。(量子統計物理学は不要)
章立ては次のとおり。
第1章:はしがき
第2章:ゴムおよびゴム類似物質
第3章:ゴム状態の本質
第4章:統計力学的な基礎
第5章:理想ゴムの統計力学的理論
第6章:実際のゴム
第7章:ゴムの理論に関連した諸問題
第1章と第2章で、ゴムを形成する分子の構造やその結合の仕方、生ゴムと硫黄を加えた「加硫ゴム」の分子構造、ゴムに類似した物質について解説がされる。
弾性をもつ原因は金属とゴムでは全く違うのだ。ゴムは固体に分類されるが、その状態は半ば液体といってもよいものであり、鎖状に結合した高分子(分子量は20万から30万)は、ゴムの伸長によりその位置を変えているのである。ゴムの弾性は物理的には熱力学的(エントロピー的)な現象であり、つまり熱力学によって定式化されるだけでなく、統計力学を使って記述することもできる。
生ゴムの分子の結合状態の一例
![]()
加硫したゴムの分子(硫黄はSであらわされる)
![]()
第3章では、ゴム弾性がエントロピー的な現象であることを踏まえて、それをもたらすのがミクロブラウン運動とマクロブラウン運動、分子内回転であることを解説し、実際に計算をしてみせてくれる。物理モデルから構成するのは熱力学の方程式だから温度変数も含まれている。つまりゴムの温度が張力にどのように影響するということもわかるわけだ。ご存じのようにゴムを冷やせば固くなる。ゴム温めれば張力は減ることが理論からも示される。
第4章では統計力学を使った解析を行うための物理モデルを提案し、これに従って鎖状分子のエントロピーを計算する。
第5章では、理想ゴム状態というもの(理想気体に対応するような形で)を定義し、マクロな力学系からの視点でゴム弾性の記述を試みる。その際、W.Kuhnの理論として知られるゴム弾性の初期の理論を説明し、その誤りを指摘している。そのうえで理論上計算されるゴムのポアソン比とヤング率の比較を行い、久保先生の理論のほうが勝っていることが示される。またこの章では高分子の網状構造をモデルにした理論、内部エネルギーを考慮した理論、運動論的なモデルを利用したゴム弾性の解釈などさまざまなモデルや視点にたってゴムの性質の理解を試みている。
![]()
第6章からは実際のゴムの性質についての考察を深める。実際のゴムとは生ゴムと加硫したゴムのことである。ゴムは伸長するとその一部が結晶化するという性質もある。低温にさらすと状態が変わるし、伸ばしたまま時間を経過させても性質が変わる。このような現象を実験と理論の両面から考察する。
第7章は「ゴムの理論に関連した諸問題」と題して、ゴムを構成する鎖状の分子がよじれて回転する場合の理論的な計算、粘性、膨潤など現象を説明し、解析を試みる。
以上のような流れで話が進むわけであるが、化学を理解していない僕でもついていけるのがうれしかった。ゴムは高分子でできているのだからまず化学を学ぶ必要があるのかなと思っていたからだ。
上の概要をお読みになっていただいてわかるように、ゴムの性質についてはすべてが解明されているわけではない。それでも、熱力学・統計力学を使った考察だけで、金属バネとは明らかに違うゴムの弾性が説明可能であることに僕は驚かされたというわけだ。
本書で紹介される理論が現実のゴムの現象にどれだけ肉薄しているかは、以下に示すグラフから感じ取ってほしい。
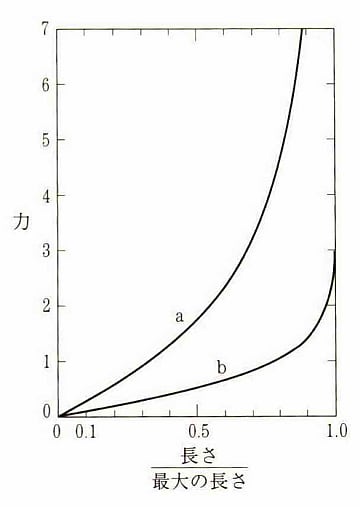
統計力学的に導かれるゴムの張力と伸びの関係(aとbは力学的モデルの違いによる)
![]()
張力と伸びの関係(理論と実験の結果)
![]()
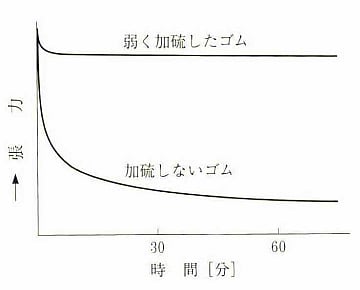
加硫の違いによる張力の緩和の時間的変化
![]()
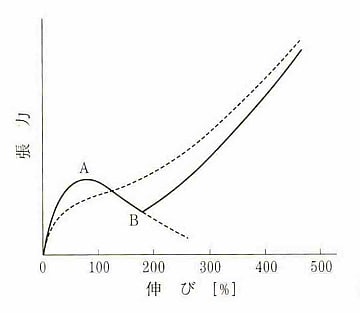
生ゴムの張力と伸びの関係(理論-実線と実際-破線の結果)
![]()
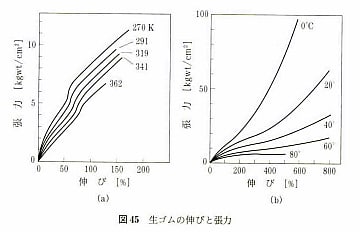
生ゴムの張力と伸びの関係の実験、温度による違い(左右のグラフは異なる実験者による実験結果)
![]()
ゴムが他の物質と極めて異質であることや魅力的な研究テーマであることは、本書のまえがきに相当する文章の中で物理学者の伏見康治先生がお書きになっている次の文章で見事に表現されている。みなさんも本書をお読みになり、この不思議さに基礎物理学の知識を使って果敢に挑んだ若き日の久保先生の物理現象に対する勘のよさと洞察力、卓越した応用力を味わってみてほしい。
------- 引用 ---------
ゴムという物質は極めて奇妙な物質である。金属の針金も引っ張れば伸びるが、それは極めてわずかである。ところがゴムは、特に加硫と言って、硫黄を入れたゴムは非常によく、2倍にも3倍近くにも伸びて、しかも手を離せば、もとの長さにもどってしまう。金属の針金も無理に引き延ばせば、今度はもとに戻らなくなってしまう。
もう一つ不思議な点がある。ゴムのバンドを急に引き延ばして唇にあててみると、それが熱くなっているのに気づく。これは気体を急に膨張させたときに冷えるのと対照的な話である。これは分子運動論的物性論の研究者にとって極めて挑戦的な問題ではなかろうか。
しかし純粋に学問的に考えても、ゴムほど分子論的物性論者にとって魅惑的な課題はなかった。若い久保亮五さんがこの問題にとりつかれたのは全く自然な話である。その熱的性質から言って、ゴムの弾性はバネの弾性のような力学的なものではなくて、熱的なものであることは明らかである。ゴムを作る分子はいわゆる高分子であって、長い、極めて長い鎖状の分子なのであって、それがくねくね折れ曲がりしている。その自由度が、伸びたときに減るから、熱が出てくるのである。
こういう立場で、久保さんは、前駆者Kuhnの誤りを訂正しながら、理論を構成していったのである。その際の武器は、熱力学と統計力学である。本書は統計力学の教科書としても良くできている。
半世紀前に書かれたこの本は、今日でも若い学徒たちへの入門書として、極めて高い価値をもっていると思う。それは著者自身が、ゴム弾性の神秘をあばこうとして、あれこれと構想をめぐらしている。その姿が如実に文間に現れているからである。
-----------------------
関連書籍:
熱力学、統計力学の名著といえば、久保先生によるこの本が筆頭だ。通読は困難だが折に触れて学び続けていたい座右の書である。
「大学演習 熱学・統計力学:久保亮五」
![]()
数式が苦手な方にはこの本をお勧めする。ゴムの弾性のしくみが理解できるだけでなく、現代の社会で使われているさまざまなゴムについて知ることができる。一般向けの科学教養書だ。
「ゴムはなぜ伸びる?―500年前、コロンブスが伝えた「新」素材の衝撃:伊藤眞義」
![]()
余談:「ゴムはなぜ伸びる?」のほうは東京理科大学・坊っちゃん選書のうちの1冊。この記事の前に紹介した「「昭和天皇実録」の謎を解く (文春新書)」の「余談」にも書いたのだが、このところ僕はどうも夏目漱石にご縁があるような気がしてならない。
応援クリックをお願いします!
![にほんブログ村 科学ブログ 物理学へ]()
![人気ブログランキングへ]()
![]()
![]()
![]()
![]()
![]()
「ゴム弾性(初版復刻版):久保亮五」
![]()
久保亮五「ゴム弾性」のもつ意義[伏見康治]
はしがき
第1章:はしがき
- 高分子物性論の位置
第2章:ゴムおよびゴム類似物質
- ゴムとその特質
- 高弾性
- ゴムの分子および加硫
- ゴムのX線的研究
- ゴム類似物質
第3章:ゴム状態の本質
- 物質の構造、原子分子間の力と力学的性質
- ミクロブラウン運動とマクロブラウン運動
- 分子内回転
- ゴム弾性の本質
- 熱力学的関係式と実験的証明
第4章:統計力学的な基礎
- 統計力学の基礎
- 理想気体
- 一つの力学的模型
- 鎖状分子のエントロピー
第5章:理想ゴムの統計力学的理論
- 理想ゴム状態
- 荷重と張力
- W.Kuhnの理論
- Poisson比とYoung率
- 網状構造の理論
- 内部エネルギーを考えた理論
- 要素分子の配向
- ゴムの張力の一つの運動論的解釈
- ゴムの複屈折
- 分子バネの説
第6章:実際のゴム
- 生ゴムの弾性
- 結晶化現象
- ゴムの低温における状態変化
- 時間的な現象および可塑性
第7章:ゴムの理論に関連した諸問題
- 分子内回転と鎖状分子の形
- 粘度
- 膨潤
- 繊維状タンパク質の問題
- 結びの言葉
付録
復刻版あとがき[西敏夫]
索引
内容紹介:
本書の初版は1947年に刊行され、その後絶版となりましたが、発刊翌年に毎日出版文化賞を受賞し、著者が若くして表された、現在でも学問的にきわめて価値の高い幻の名著として今日まで語り継がれてまいりました。
著者は1995年3月に亡くなられましたが、著者の業績を忍ぶ各方面から復刊の要望が高く、読みやすい現代版として復刻したものです。
ゴムの物理や化学は今日でもなお未解決の問題も多く、当時少壮気鋭の学者としてこの問題に取り組まれた著者の、ゴム弾性の神秘をあばこうとして構想をめぐらす姿勢がうかがわれる本書は、直接この方面に携わる方々を魅了するばかりでなく、多くの方々の興奮を呼び起こすことでありましょう。復刻版は1996年6月刊行、176ページ。
著者について:
久保亮五(くぼりょうご):ウィキペディアの記事
1920年 東京に生まれる。東京大学教授、京都大学教授、慶應大学教授、日本物理学会会長などを歴任。東京大学名誉教授、理学博士。統計物理学、物性物理学の分野で国際的に知られた。 特に線形応答理論の構築に貢献し、彼の提案した理論は「久保理論」の名でも呼ばれている。 1997年に生前の業績を記念して井上科学振興財団が久保亮五記念賞を創設した。
久保先生の著書、訳書: Amazonで検索する
理数系書籍のレビュー記事は本書で285冊目。
小学校ではバネにおもりを吊るす実験をして張力とバネの伸びが比例するという「フックの法則」を学ぶ。僕はこの実験をしたとき、バネではなくてゴムを使っても同じになるのかなと思って試してみたことがある。輪ゴムをいくつもつないでバネのかわりにして、おもりのかわりに10円玉を何枚も使って実験した。
その当時、八百屋さんでは「ばね秤」が使われていたけれども、子供たちの身の回りにあってすぐ手に入るのは輪ゴムや女の子たちが「ゴム段」で遊ぶために使っていた長いゴムの輪だった。どちらも日常的に目にしていたものだから、僕がゴムを使って秤を作ってみたらと思いついたのは自然なことだ。
実験の記録はノートに書かなかったので詳しいことは忘れてしまったが、伸びの長さと張力が比例していなかったことだけは覚えている。なぜなのだろう?と先生に聞いてみたことも覚えているが、当時教えていただいた先生は理数系の大学で学んでいない若い女の先生だったので、今になって思うと先生に答えられたはずがない。
結果がどうなるのか、ネットで調べてみたところ次のようになることがわかった。
点線は初めて引っ張ったときの伸びと張力の関係、実線は10回ほどゴムを伸ばしたり元に戻したりした後に測定した伸びと張力の関係である。

輪ゴムで身近なものの質量を量る
http://www.ons.ne.jp/~taka1997/education/2012/1-physics/14/
注意:このページではフックの法則を無理矢理あてはめてグラフを直線化させてしまっているが、測定値を見る限りフックの法則は成り立っていないと僕は思う。もちろんどんな曲線であっても部分的には直線に近似できるわけだが。物理は初めに法則ありきではない。現実の結果を最優先すべきである。縦と横の軸がこのブログ記事のグラフと逆になっていることにも注意。
けれども僕にできることはそこまでで、それ以来、現在に至るまでゴムがなぜ「フックの法則」に従わないのか、どのようなしくみで伸びるのかは謎のままだった。そしてこの10年ほど物理学を学んできたが、この話題に触れている本はひとつもなかった。ゴムについて僕はほとんど何も知らない。僕にとってゴムは知識の平原の中にぽっかり空いている「無知の穴」のようなものだ。
要素還元主義を無理矢理こじつければ、ゴムの弾性は4つの力のうち電磁気力によるものだろうけれど、それでは安直すぎる。ファンデルワールス力(分子間力)も関係していそうだし。(実際、条件によっては関係しているのだ。)
その後、ゴムは繊維状の高分子の集合体であり、ほつれた毛糸の塊を伸ばすようなイメージで伸びるのだと感覚的にとらえるようになったが、これも定性的な理解をしているに過ぎないわけで。。。
相対性理論や量子力学、素粒子物理学などの基礎物理学も大事だけど、身の回りの物のしくみも知っておくのも大切だから今年は物性物理を学び始めている。ゴムのしくみは高分子物性物理だ。
本書はこのテーマについて統計物理学、物性物理学の大家でいらっしゃる久保亮五先生が27歳のときに研究成果をまとめて出版された本である。初版が刊行されたのは1947年で、1996年に復刻版として刊行された名著だ。久保先生の処女作でもある。
ゴムの弾性について定性的な理解が深まるだけでなく、いくつかの物理モデルに従った理論にもとづいた定式化により、定量的な理解も深めることができる。前提知識として熱力学、統計力学が必要になる。(量子統計物理学は不要)
章立ては次のとおり。
第1章:はしがき
第2章:ゴムおよびゴム類似物質
第3章:ゴム状態の本質
第4章:統計力学的な基礎
第5章:理想ゴムの統計力学的理論
第6章:実際のゴム
第7章:ゴムの理論に関連した諸問題
第1章と第2章で、ゴムを形成する分子の構造やその結合の仕方、生ゴムと硫黄を加えた「加硫ゴム」の分子構造、ゴムに類似した物質について解説がされる。
弾性をもつ原因は金属とゴムでは全く違うのだ。ゴムは固体に分類されるが、その状態は半ば液体といってもよいものであり、鎖状に結合した高分子(分子量は20万から30万)は、ゴムの伸長によりその位置を変えているのである。ゴムの弾性は物理的には熱力学的(エントロピー的)な現象であり、つまり熱力学によって定式化されるだけでなく、統計力学を使って記述することもできる。
生ゴムの分子の結合状態の一例

加硫したゴムの分子(硫黄はSであらわされる)

第3章では、ゴム弾性がエントロピー的な現象であることを踏まえて、それをもたらすのがミクロブラウン運動とマクロブラウン運動、分子内回転であることを解説し、実際に計算をしてみせてくれる。物理モデルから構成するのは熱力学の方程式だから温度変数も含まれている。つまりゴムの温度が張力にどのように影響するということもわかるわけだ。ご存じのようにゴムを冷やせば固くなる。ゴム温めれば張力は減ることが理論からも示される。
第4章では統計力学を使った解析を行うための物理モデルを提案し、これに従って鎖状分子のエントロピーを計算する。
第5章では、理想ゴム状態というもの(理想気体に対応するような形で)を定義し、マクロな力学系からの視点でゴム弾性の記述を試みる。その際、W.Kuhnの理論として知られるゴム弾性の初期の理論を説明し、その誤りを指摘している。そのうえで理論上計算されるゴムのポアソン比とヤング率の比較を行い、久保先生の理論のほうが勝っていることが示される。またこの章では高分子の網状構造をモデルにした理論、内部エネルギーを考慮した理論、運動論的なモデルを利用したゴム弾性の解釈などさまざまなモデルや視点にたってゴムの性質の理解を試みている。

第6章からは実際のゴムの性質についての考察を深める。実際のゴムとは生ゴムと加硫したゴムのことである。ゴムは伸長するとその一部が結晶化するという性質もある。低温にさらすと状態が変わるし、伸ばしたまま時間を経過させても性質が変わる。このような現象を実験と理論の両面から考察する。
第7章は「ゴムの理論に関連した諸問題」と題して、ゴムを構成する鎖状の分子がよじれて回転する場合の理論的な計算、粘性、膨潤など現象を説明し、解析を試みる。
以上のような流れで話が進むわけであるが、化学を理解していない僕でもついていけるのがうれしかった。ゴムは高分子でできているのだからまず化学を学ぶ必要があるのかなと思っていたからだ。
上の概要をお読みになっていただいてわかるように、ゴムの性質についてはすべてが解明されているわけではない。それでも、熱力学・統計力学を使った考察だけで、金属バネとは明らかに違うゴムの弾性が説明可能であることに僕は驚かされたというわけだ。
本書で紹介される理論が現実のゴムの現象にどれだけ肉薄しているかは、以下に示すグラフから感じ取ってほしい。
統計力学的に導かれるゴムの張力と伸びの関係(aとbは力学的モデルの違いによる)
張力と伸びの関係(理論と実験の結果)

加硫の違いによる張力の緩和の時間的変化
生ゴムの張力と伸びの関係(理論-実線と実際-破線の結果)
生ゴムの張力と伸びの関係の実験、温度による違い(左右のグラフは異なる実験者による実験結果)
ゴムが他の物質と極めて異質であることや魅力的な研究テーマであることは、本書のまえがきに相当する文章の中で物理学者の伏見康治先生がお書きになっている次の文章で見事に表現されている。みなさんも本書をお読みになり、この不思議さに基礎物理学の知識を使って果敢に挑んだ若き日の久保先生の物理現象に対する勘のよさと洞察力、卓越した応用力を味わってみてほしい。
------- 引用 ---------
ゴムという物質は極めて奇妙な物質である。金属の針金も引っ張れば伸びるが、それは極めてわずかである。ところがゴムは、特に加硫と言って、硫黄を入れたゴムは非常によく、2倍にも3倍近くにも伸びて、しかも手を離せば、もとの長さにもどってしまう。金属の針金も無理に引き延ばせば、今度はもとに戻らなくなってしまう。
もう一つ不思議な点がある。ゴムのバンドを急に引き延ばして唇にあててみると、それが熱くなっているのに気づく。これは気体を急に膨張させたときに冷えるのと対照的な話である。これは分子運動論的物性論の研究者にとって極めて挑戦的な問題ではなかろうか。
しかし純粋に学問的に考えても、ゴムほど分子論的物性論者にとって魅惑的な課題はなかった。若い久保亮五さんがこの問題にとりつかれたのは全く自然な話である。その熱的性質から言って、ゴムの弾性はバネの弾性のような力学的なものではなくて、熱的なものであることは明らかである。ゴムを作る分子はいわゆる高分子であって、長い、極めて長い鎖状の分子なのであって、それがくねくね折れ曲がりしている。その自由度が、伸びたときに減るから、熱が出てくるのである。
こういう立場で、久保さんは、前駆者Kuhnの誤りを訂正しながら、理論を構成していったのである。その際の武器は、熱力学と統計力学である。本書は統計力学の教科書としても良くできている。
半世紀前に書かれたこの本は、今日でも若い学徒たちへの入門書として、極めて高い価値をもっていると思う。それは著者自身が、ゴム弾性の神秘をあばこうとして、あれこれと構想をめぐらしている。その姿が如実に文間に現れているからである。
-----------------------
関連書籍:
熱力学、統計力学の名著といえば、久保先生によるこの本が筆頭だ。通読は困難だが折に触れて学び続けていたい座右の書である。
「大学演習 熱学・統計力学:久保亮五」

数式が苦手な方にはこの本をお勧めする。ゴムの弾性のしくみが理解できるだけでなく、現代の社会で使われているさまざまなゴムについて知ることができる。一般向けの科学教養書だ。
「ゴムはなぜ伸びる?―500年前、コロンブスが伝えた「新」素材の衝撃:伊藤眞義」

余談:「ゴムはなぜ伸びる?」のほうは東京理科大学・坊っちゃん選書のうちの1冊。この記事の前に紹介した「「昭和天皇実録」の謎を解く (文春新書)」の「余談」にも書いたのだが、このところ僕はどうも夏目漱石にご縁があるような気がしてならない。
応援クリックをお願いします!







「ゴム弾性(初版復刻版):久保亮五」

久保亮五「ゴム弾性」のもつ意義[伏見康治]
はしがき
第1章:はしがき
- 高分子物性論の位置
第2章:ゴムおよびゴム類似物質
- ゴムとその特質
- 高弾性
- ゴムの分子および加硫
- ゴムのX線的研究
- ゴム類似物質
第3章:ゴム状態の本質
- 物質の構造、原子分子間の力と力学的性質
- ミクロブラウン運動とマクロブラウン運動
- 分子内回転
- ゴム弾性の本質
- 熱力学的関係式と実験的証明
第4章:統計力学的な基礎
- 統計力学の基礎
- 理想気体
- 一つの力学的模型
- 鎖状分子のエントロピー
第5章:理想ゴムの統計力学的理論
- 理想ゴム状態
- 荷重と張力
- W.Kuhnの理論
- Poisson比とYoung率
- 網状構造の理論
- 内部エネルギーを考えた理論
- 要素分子の配向
- ゴムの張力の一つの運動論的解釈
- ゴムの複屈折
- 分子バネの説
第6章:実際のゴム
- 生ゴムの弾性
- 結晶化現象
- ゴムの低温における状態変化
- 時間的な現象および可塑性
第7章:ゴムの理論に関連した諸問題
- 分子内回転と鎖状分子の形
- 粘度
- 膨潤
- 繊維状タンパク質の問題
- 結びの言葉
付録
復刻版あとがき[西敏夫]
索引