絡まってしまったネックレス
ひもが絡まるのは3次元空間だけ
前回の記事までの説明で、空間の中で絡んでしまうのは、空間の次元より2つ小さい次元の物体であることがご理解いただけたと思います。だから3次元空間で絡まるのは1次元のひもだけなのです。
2次元空間、すなわち平面ではひもが絡まないことは簡単にわかりますよね?平面内しか動けないひもは交差できないからです。
![]()
でも3次元空間で絡んでいるひもは、4次元空間ではどうなるのでしょう?
実をいうとひもは絡まずに簡単にほどけてしまうのです。というより3次元空間では絡んでいるひもは、その3次元空間を含んでいる4次元空間の中では絡んでいないのです。
今日はそのことをご説明いたしましょう。
第2回の記事で、このような写真をお見せしました。
![]()
これは2次元空間で絡んでいる「ひもと点」です。2次元空間でひもは交差することができませんから、絡んでいる状態を無理矢理作ったのだとご理解ください。写真の撮り方が悪くて青いひもの端が面から浮いてしまっていますが、本当は面にぴったりくっついている写真を撮りたかったのです。
2次元空間の縦と横のどの方向に引っ張っても、青いひもは赤い点にさえぎられてしまい、絡みをほどくことはできません。ほどくためには再びひもを上の方向に持ち上げないとなりませんから駄目です。ひもを持ち上げることは禁止されています。
けれども3次元空間にいる私たちの立場から見るとどうでしょうか?ひもを持ち上げれば簡単にはずせますね。このようにするわけです。
![]()
上の面と下の面は2次元空間のパラレルワールドです。下の空間から突如として青いひもは消えてしまい、上の空間に移動します。上の空間で青いひもを横にずらして、再び下に移動させれば下の空間で赤い点と青いひもは離れた場所に置かれていることになります。
3次元空間では、もともとひもと点は絡まっていなかったので、上方向すなわちZ軸の方向の移動を使って絡まりをほどくことに成功したのです。
同じ方法を使って3次元空間で絡まっているひもをほどくことができます。どんなに複雑に絡まっていても大丈夫です。
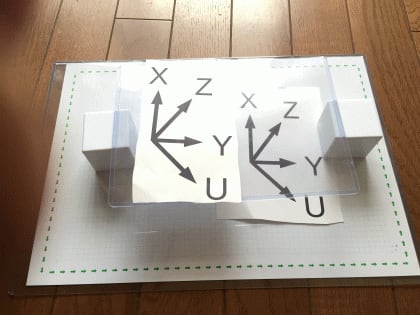
第3回の記事で紹介した4次元空間に浮かぶ3次元空間のパラレルワールドはこのようなものでした。写真には書いてありませんが上方向がU軸が延びている方向です。
![]()
3次元空間に絡まった状態のひもを用意します。3次元空間内でほどくことは可能ですが容易ではありません。
![]()
そして青いひもを4次元空間内でU軸の方向に持ち上げます。この写真ではわかりませんが、U軸方向では青いひもは赤いひもにぶつからなくてすむので持ち上げることができるのです。このとき下の3次元空間から青いひもは一瞬で消滅します。
![]()
それから青いひもを上の3次元空間内でそのまま右にずらし、ふたたびU軸にそって下に移動させれば、もとの3次元空間に戻ります。赤と青の糸はもう絡んではいません。
4次元空間ではもともとひもは絡んでいないから、このようなことができるのです。
4次元空間で絡んでいる2次元物体も5次元空間のV軸方向に移動させれば、ほどくことができます。
![]()
5次元空間で絡んでいる3次元物体も6次元空間のW軸方向に移動させれば、ほどくことができます。
![]()
![]()
「なんだそんなことか。」と拍子抜けしてしまった方がいるかもしれませんね。僕もあまり面白いとは思いませんでした。要するにこういうことです。
「ある次元の空間で絡んでいる物体をほどくためには、そのひとつ上の次元の空間の座標軸の方向に移動すればよい。」
というわけです。また、次のように言ってもよいでしょう。
「ある次元の物体が絡んでいるときは、その物体の曲がりの自由度が3になるような空間の次元の座標軸の方向に移動すればよい。」
1次元のひもが絡んでいるときは1+3=4、つまり4次元空間を利用すればよいわけです。
これが私たちが知りえた多次元空間で成り立つ常識です。
ここでこの記事を終えることができれば、みなさんも「ああ、そういうことだったのか。」と安心して読み終えることができたはずですし僕もそれを望んでいました。しかし、とんでもないことを僕は見つけてしまったのです。
ウィキペディアの「結び目理論」の項目の中で「高次元結び目・絡み目」のところに次のようなことが書かれています。
![]()
高次元空間での高次元物体の結び目が研究されていることにも驚きましたが、僕が特に驚いたのは「いずれもm=n+2の場合もm>n+2の場合も研究されている。」の部分です。
ウィキペディアに書かれていることの一部を、私たちの言葉に翻訳すると次のようになります。
「高次元絡み目とはm次元の空間の中にあるn次元の物体の絡みを研究する。mはnより2以上大きい。m=n+2の場合もm>n+2の場合も研究されている。」
私たちが知りえた多次元空間の常識で物体が絡むのは「m=n+2」のときだけでしたよね。2が曲がりの自由度なのですから。m次元空間で絡むのはm-2次元の物体だけのはずです。
ところがここには「曲がりの自由度が2より大きい」ときの絡みの研究が行われていると書かれているわけです。たったひとつの等号が不等号に変わるだけで世界は大きく変わってしまします。
つまり、この記述は絡んでいる物体をほどくために次元数が2つ大きい空間を使ってもできないことがあるのだと言っています。それは曲がりの自由度が3以上でも絡んでしまう物体があるということと同じです。
どのようなときに絡みをほどくことができて、どのようなときにできないか、どこまで次元の高い空間を利用すれば絡みがほどけるのか、そして曲がりの自由度が3以上のときにおきる物体が絡む現象がどのようなものであるかはこの理論を研究しないとわかりません。
ともかく、私たちの常識が成り立たない状況がずっと高次元の空間にあることがわかりました。
なんというか、多次元空間は奥が深いというか、思わぬところに不思議がぽっかり口を開けている感じがします。結び目理論を学んでいない僕には、今のところ手も足も出ません。
中学生、高校生にも理解していただけるように説明すると第1回の記事で書きましたが、ここだけは勘弁してください。
引用箇所の最後には「高次元結び目・絡み目の場合、1次元結び目・絡み目と違った興味深い現象も少なくなく、excitingな研究テーマの一つである。」と書いてあります。興味を持たれた方はいつか結び目理論に挑戦してみてください。
arxiv1304.6053 Introduction to high dimensional knots: Eiji Ogasa
高次元結び目・絡み目の初心者向けの入門記事(2013年の論文):PDFファイル
A survey of applications of surgery to knot and link theory: J Levine, K Orr - Ann. of Math. Stud, 2000
高次元結び目・絡み目の上級者向けの入門記事(2000年の論文):PDFファイル
さて、次回の記事では「モノはどのように曲がる?」について説明します。もちろん多次元空間での話です。
関連記事:
多次元空間へのお誘い(1):はじめに
http://blog.goo.ne.jp/ktonegaw/e/3c2bacd624695dcad7dd2fa9feadd5bd
多次元空間へのお誘い(2):4次元空間での布団干し
http://blog.goo.ne.jp/ktonegaw/e/81fb8e0a7f148699fcda78486f868903
多次元空間へのお誘い(3):多次元空間で絡み合うモノは?
http://blog.goo.ne.jp/ktonegaw/e/26b5ed44928e4b4148c3e71c99e401f6
多次元空間へのお誘い(4):絡まるとはどういうことか?
http://blog.goo.ne.jp/ktonegaw/e/4a3a231b3fc99a92eefc88d94f8e4fb8
応援クリックをお願いします!
![にほんブログ村 科学ブログ 物理学へ]()
![人気ブログランキングへ]()
![]()
![]()
![]()
![]()
![]()
ひもが絡まるのは3次元空間だけ
前回の記事までの説明で、空間の中で絡んでしまうのは、空間の次元より2つ小さい次元の物体であることがご理解いただけたと思います。だから3次元空間で絡まるのは1次元のひもだけなのです。
2次元空間、すなわち平面ではひもが絡まないことは簡単にわかりますよね?平面内しか動けないひもは交差できないからです。

でも3次元空間で絡んでいるひもは、4次元空間ではどうなるのでしょう?
実をいうとひもは絡まずに簡単にほどけてしまうのです。というより3次元空間では絡んでいるひもは、その3次元空間を含んでいる4次元空間の中では絡んでいないのです。
今日はそのことをご説明いたしましょう。
第2回の記事で、このような写真をお見せしました。

これは2次元空間で絡んでいる「ひもと点」です。2次元空間でひもは交差することができませんから、絡んでいる状態を無理矢理作ったのだとご理解ください。写真の撮り方が悪くて青いひもの端が面から浮いてしまっていますが、本当は面にぴったりくっついている写真を撮りたかったのです。
2次元空間の縦と横のどの方向に引っ張っても、青いひもは赤い点にさえぎられてしまい、絡みをほどくことはできません。ほどくためには再びひもを上の方向に持ち上げないとなりませんから駄目です。ひもを持ち上げることは禁止されています。
けれども3次元空間にいる私たちの立場から見るとどうでしょうか?ひもを持ち上げれば簡単にはずせますね。このようにするわけです。

上の面と下の面は2次元空間のパラレルワールドです。下の空間から突如として青いひもは消えてしまい、上の空間に移動します。上の空間で青いひもを横にずらして、再び下に移動させれば下の空間で赤い点と青いひもは離れた場所に置かれていることになります。
3次元空間では、もともとひもと点は絡まっていなかったので、上方向すなわちZ軸の方向の移動を使って絡まりをほどくことに成功したのです。
同じ方法を使って3次元空間で絡まっているひもをほどくことができます。どんなに複雑に絡まっていても大丈夫です。
第3回の記事で紹介した4次元空間に浮かぶ3次元空間のパラレルワールドはこのようなものでした。写真には書いてありませんが上方向がU軸が延びている方向です。

3次元空間に絡まった状態のひもを用意します。3次元空間内でほどくことは可能ですが容易ではありません。

そして青いひもを4次元空間内でU軸の方向に持ち上げます。この写真ではわかりませんが、U軸方向では青いひもは赤いひもにぶつからなくてすむので持ち上げることができるのです。このとき下の3次元空間から青いひもは一瞬で消滅します。

それから青いひもを上の3次元空間内でそのまま右にずらし、ふたたびU軸にそって下に移動させれば、もとの3次元空間に戻ります。赤と青の糸はもう絡んではいません。
4次元空間ではもともとひもは絡んでいないから、このようなことができるのです。
4次元空間で絡んでいる2次元物体も5次元空間のV軸方向に移動させれば、ほどくことができます。
5次元空間で絡んでいる3次元物体も6次元空間のW軸方向に移動させれば、ほどくことができます。


「なんだそんなことか。」と拍子抜けしてしまった方がいるかもしれませんね。僕もあまり面白いとは思いませんでした。要するにこういうことです。
「ある次元の空間で絡んでいる物体をほどくためには、そのひとつ上の次元の空間の座標軸の方向に移動すればよい。」
というわけです。また、次のように言ってもよいでしょう。
「ある次元の物体が絡んでいるときは、その物体の曲がりの自由度が3になるような空間の次元の座標軸の方向に移動すればよい。」
1次元のひもが絡んでいるときは1+3=4、つまり4次元空間を利用すればよいわけです。
これが私たちが知りえた多次元空間で成り立つ常識です。
ここでこの記事を終えることができれば、みなさんも「ああ、そういうことだったのか。」と安心して読み終えることができたはずですし僕もそれを望んでいました。しかし、とんでもないことを僕は見つけてしまったのです。
ウィキペディアの「結び目理論」の項目の中で「高次元結び目・絡み目」のところに次のようなことが書かれています。

高次元空間での高次元物体の結び目が研究されていることにも驚きましたが、僕が特に驚いたのは「いずれもm=n+2の場合もm>n+2の場合も研究されている。」の部分です。
ウィキペディアに書かれていることの一部を、私たちの言葉に翻訳すると次のようになります。
「高次元絡み目とはm次元の空間の中にあるn次元の物体の絡みを研究する。mはnより2以上大きい。m=n+2の場合もm>n+2の場合も研究されている。」
私たちが知りえた多次元空間の常識で物体が絡むのは「m=n+2」のときだけでしたよね。2が曲がりの自由度なのですから。m次元空間で絡むのはm-2次元の物体だけのはずです。
ところがここには「曲がりの自由度が2より大きい」ときの絡みの研究が行われていると書かれているわけです。たったひとつの等号が不等号に変わるだけで世界は大きく変わってしまします。
つまり、この記述は絡んでいる物体をほどくために次元数が2つ大きい空間を使ってもできないことがあるのだと言っています。それは曲がりの自由度が3以上でも絡んでしまう物体があるということと同じです。
どのようなときに絡みをほどくことができて、どのようなときにできないか、どこまで次元の高い空間を利用すれば絡みがほどけるのか、そして曲がりの自由度が3以上のときにおきる物体が絡む現象がどのようなものであるかはこの理論を研究しないとわかりません。
ともかく、私たちの常識が成り立たない状況がずっと高次元の空間にあることがわかりました。
なんというか、多次元空間は奥が深いというか、思わぬところに不思議がぽっかり口を開けている感じがします。結び目理論を学んでいない僕には、今のところ手も足も出ません。
中学生、高校生にも理解していただけるように説明すると第1回の記事で書きましたが、ここだけは勘弁してください。
引用箇所の最後には「高次元結び目・絡み目の場合、1次元結び目・絡み目と違った興味深い現象も少なくなく、excitingな研究テーマの一つである。」と書いてあります。興味を持たれた方はいつか結び目理論に挑戦してみてください。
arxiv1304.6053 Introduction to high dimensional knots: Eiji Ogasa
高次元結び目・絡み目の初心者向けの入門記事(2013年の論文):PDFファイル
A survey of applications of surgery to knot and link theory: J Levine, K Orr - Ann. of Math. Stud, 2000
高次元結び目・絡み目の上級者向けの入門記事(2000年の論文):PDFファイル
さて、次回の記事では「モノはどのように曲がる?」について説明します。もちろん多次元空間での話です。
関連記事:
多次元空間へのお誘い(1):はじめに
http://blog.goo.ne.jp/ktonegaw/e/3c2bacd624695dcad7dd2fa9feadd5bd
多次元空間へのお誘い(2):4次元空間での布団干し
http://blog.goo.ne.jp/ktonegaw/e/81fb8e0a7f148699fcda78486f868903
多次元空間へのお誘い(3):多次元空間で絡み合うモノは?
http://blog.goo.ne.jp/ktonegaw/e/26b5ed44928e4b4148c3e71c99e401f6
多次元空間へのお誘い(4):絡まるとはどういうことか?
http://blog.goo.ne.jp/ktonegaw/e/4a3a231b3fc99a92eefc88d94f8e4fb8
応援クリックをお願いします!






