「固体物理の基礎 上・1 固体電子論概論： アシュクロフト、マーミン」
内容紹介：
学部生にも大学院生にも使えるよう工夫され、内容の取捨選択がしやすく、種々の目的､異なる水準でもうまく使い分けられる。固体物理学の現象の記述と理論的解析による統一という著者の目標は完全に達成されている。1981年刊行、309ページ。
著者について：
ニール・W・アシュクロフト（ウィキペディア、経歴詳細）
イギリスの物理学者（固体物理学）、1938年生。1958年ニュージーランド大学卒業。学位は1964年ケンブリッジ大学。シカゴ大学およびコーネル大学で博士研究員、1975年教授。1990年にHorace White Professor of Physics。2006年名誉教授。
デヴィッド・マーミン（ウィキペディア、ホームページ）
コーネル大学名誉教授（物理学）。米国物理学会のリリエンフェルト賞および米国物理教育学会のクロプステッグ賞を受賞。米国科学アカデミー、米国芸術科学アカデミーの会員。この数十年の間に、量子論の基礎的な問題に関する多くの著作を執筆しており、科学の啓蒙に関する明瞭さと機知には定評がある。
訳者について：
松原武生（まつばらたけお）
1921-2014 昭和後期-平成時代の理論物理学者。
大正10年4月3日生まれ。北大教授をへて昭和30年京大教授となる。61年岡山理大教授。誘電体、超伝導、超流動などを研究。「温度グリーン関数」の概念を提案した。36年仁科記念賞。日本物理学会会長をつとめた。平成26年12月15日死去。93歳。大阪府出身。大阪帝大卒。著作に「超流動と超伝導」「固体物理学」など。
町田一成（まちだかずしげ）
1968年東京教育大学理学部卒業。1973年同上理学研究科博士課程修了。京都大学理学部助手、岡山大学理学部助教授、教授を経て、岡山大学大学院自然科学研究科教授。
理数系書籍のレビュー記事は本書で272冊目。
ようやくこの大著に取りかかることができた。固体物理学に本格的に入門するのだ。
「新年のご挨拶」の記事の冒頭で「すでに買い置きしてある入門書レベルの教科書を１冊読んで、その後はアシュクロフト＆マーミンの「固体物理学の基礎」の４冊を読んでみたいです。」と僕は宣言していた。３ヶ月たってようやくこの名著に取り掛かることができた。
学部で学ぶ固体物理の定番の教科書といえば「キッテル固体物理学入門」が有名だが、アマゾンでの評判は日本語版、英語版ともによろしくない。
また新しい教科書「グロッソの固体物理学」はアマゾンでの評価がよく、興味を持ったのだがまだ広く受け入れられていない教科書のようなので、ひととおり定番の教科書で学んでから読むことにした。
あと「物性物理」や「固体物理」というキーワードで検索すると、学部の教科書として使えるくらいのページ数の教科書がたくさん見つかる。それらの中には良書も多いのだろうけど、僕はすでに「基礎の固体物理学： 斯波弘行」という260ページの本で学んでいるので、同じようなレベルの本だと重複してしまう。
ということでページ数にこだわらず、定番中の定番であるアシュクロフト＆マーミンを読むことにした。特にアマゾンのレビューに書かれている次の２つのコメントが僕の決断を後押しした。
コメント１：
国内で出版されている物性の本で、一番分りやすい本は恐らくこの本であろう。吉岡書店からこのシリーズは計4冊出版されているが、その最も基礎的なトピックをまとめたのがこの一冊である。内容としては、電気伝導性の古典論から始まり、量子論の導入、逆格子、そしてバンド計算の方法へと展開していく内容で、物性物理の歴史的な流れに沿っている。
コメント２：
本書は文学作品のように一つのストーリーとして構成されています。頭から読み進めていき、この先はどうなるんだろうとわくわくしながらページをめくっていくような読み方をすることが筆者の意図に合っているのかもしれません。学生のときに読んだドストエフスキーのカラマーゾフの兄弟を思い出します。推理小説のような側面もあり、かつ文学作品として完璧といった感じ。周りの読んだことのある人たちに聞くと、事前に予習をしてからという人もいれば前提知識なしに読んでからもう一回読み返したという人もいました。本書を読むときにも、どうするかは読者それぞれの本の楽しみ方に任されているのでしょう。
英語版は1976年に出版され、日本語版は僕が高校を卒業した1981年に出版された。その後、新しいテーマを取り入れた形で2008年に第４巻だけが改訂されている。日本語版は次のような構成だ。
上・1 固体電子論概論 - 1981
上・2 固体のバンド理論 - 1981
下・1 固体フォノンの諸問題 - 1981
下・2 固体の物性各論 - 2008
上記のコメント１に書かれているように第１巻は最も基礎的なトピックをまとめた内容だ。とはいっても「基礎の固体物理学： 斯波弘行」では少ししか解説されていなかった結晶構造（格子）の種類についての解説がとても詳しい。
高校で物理を学んでいない人は「金属に結晶があるの？」と思うかもしれない。それは金属は「展性」という性質をもっているために水晶や塩化ナトリウムのように結晶構造をもつことが想像しにくいからだ。
塩化フタロシアニン銅の電子顕微鏡写真（解説ページ）
Image may be NSFW.
Clik here to view.
水素とバナジウムの化合物の電子顕微鏡写真（解説ページ）
Image may be NSFW.
Clik here to view.
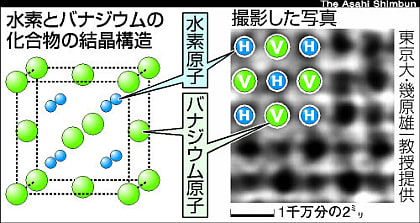
実際は金属も原子が周期的に並ぶことにより格子が繰り返されて、結晶のような形で存在している。電子ひとつひとつの挙動などわかるはずがないのに、金属のもつ性質が説明できてしまうのが固体物理学のすごいところだ。金属の元素が違えば格子構造も異なり、鉱物の結晶のように７種類に分類される。
以下、本書に掲載されている図版を載せておこう。これらの図の原典は1960年代に書かれたれた教科書や論文から本書に引用されたものだ。金属元素とひとくちに言っても、状況はさまざまであることがおわかりになるだろう。
ブラベー格子の点群対称性
(a)立方対称 (b)正方対称 (c)斜方対称 (d)単斜対称 (e)三斜対称 (f)三方対称 (g)六方対称
Image may be NSFW.
Clik here to view.
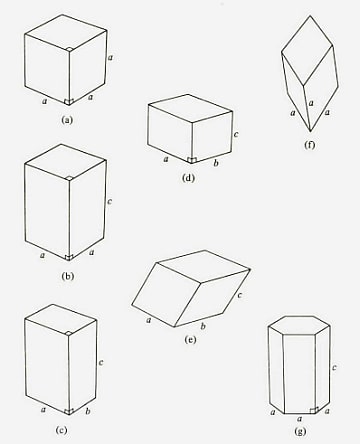
14種類あるブラベー格子の分類と結晶構造の分類
Image may be NSFW.
Clik here to view.
(a)体心立方格子の第１ブリルアン・ゾーン
(b)面心立方格子の第１ブリルアン・ゾーン
Image may be NSFW.
Clik here to view.
面心立方ブラベー格子のウィグナー・サイツ・セル（面が菱形の１２面体）
Image may be NSFW.
Clik here to view.
fccブラベー格子の自由電子エネルギー状態。Γ(k=0), K, L, W,およびX点を結ぶ第１ブリルアン・ゾーン内の方向に従ってエネルギーが示されている。横線は基本単位格子あたりの電子数に対するフェルミ・エネルギーを示す。曲線内に示された点の数はその曲線で表される自由電子状態の縮退度を表す。
Image may be NSFW.
Clik here to view.
(a)体心立方と(b)面心立方結晶に対する第１、第２、第３ブリルアン・ゾーン面。
Image may be NSFW.
Clik here to view.
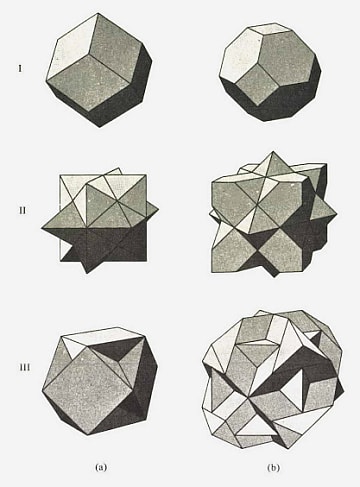
４価の面心立方金属のフェルミ球。（第１ゾーンから第４ゾーンまで）
Image may be NSFW.
Clik here to view.
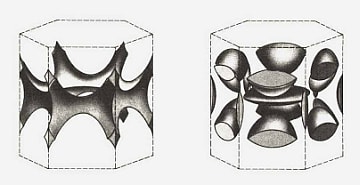
第１ブリルアン・ゾーンの水平な六角形面により互いに切り離されていた部分を集め直して得られた２価hcp金属のフェルミ面。第１と第２ゾーンを一緒にして左側の構造ができ、第３と第４ゾーン内の多くの部分から右側の構造となる。
Image may be NSFW.
Clik here to view.
章立ては次のとおりだ。「固体物理学史」にほぼ沿った流れで解説が展開される。
第１章：金属のドゥルーデ（Drude）理論
第２章：金属のゾンマーフェルト理論
第３章：自由電子モデルの破綻
第４章：結晶格子
第５章：逆格子
第６章：Ｘ線回折による結晶構造の決定
第７章：ブラベー格子の分類と結晶構造の分類
第８章：周期ポテンシャル中の電子状態、一般的性質
第９章：弱い周期ポテンシャルの中の電子
第１０章：強く束縛された方法
第１章のドゥルーデの理論は金属の電気伝導に自由電子のモデルを適用したことで知られ、調べてみたところこの理論が提唱されたのは1900年であることがわかった。（参考ページ）
電子はJ.J.トムソンが1897年に行なった陰極線の実験によって発見され、原子の存在を最終的に証明したのがアインシュタインが1905年に発表した気体の分子運動論だったので、1900年をはさんでいろいろな研究がかなり早いペースで進行していたのだ。そして量子力学的な条件を考慮したゾンマーフェルトの理論が発表されたのは1916年のことである。
だれが原子をみたか(岩波現代文庫)：江沢洋
http://blog.goo.ne.jp/ktonegaw/e/0f1e91e296d8d83ff2759c2de190be57
新版 電子と原子核の発見(ちくま学芸文庫)：S.ワインバーグ
http://blog.goo.ne.jp/ktonegaw/e/d6244b03bafe78c8c2316c91342df73e
高校までの物理学でも金属原子が格子構造をもつことや、その中の電子が動くことで電流が流れることを学ぶが、あくまで定性的なイメージでしか教えられない。また量子力学によると電子の位置は確率的にしか求められないわけだから、格子の中で電子がどのような状態で存在し、どのような運動をするのかイメージすることすらおぼつかないはずだ。
電子は格子中を移動するものもあるし、原子核に引き寄せられた（束縛された）ものもある。金属の結晶の中でそれらがどのように存在し、どのように周囲の原子核や電子から影響を受けるかを突き止めていくプロセスが第１巻で示されていることなのだ。
結晶構造が複雑になるにつれて、そして原子価が大きくなるにつれて様相は複雑さを増してくる。計算で示された結果と実際の金属元素で測定した結果を比べ、理論の正しさや不正確さを判断していくのだ。
特に僕にとって新しい学びとなったのは「第６章：Ｘ線回折による結晶構造の決定」である。X線の波長は典型的な金属元素の原子間距離に近いので、金属結晶の構造を反映した回折をおこす。知識として知っていても、実際にどのような実験をして、どのような計算をするのか、そしてどのように検証すればよいかを本書で学ぶことができる。
こういうことが２０世紀の前半に行われていたことを思うと、自然科学の学問としての威力とそれに貢献した物理学者や技術者たちの「仕事の質」に感動させられるのだ。そのための計算を計算尺や手回し計算機でしていたわけなのだから。
また、上に紹介した図はすべて手描きである。結晶や格子の構造を文章だけで理解するのはよほどの想像力、空間認識力が必要だ。本書には図版が載せられているとはいえ、その数は十分ではない。現代のコンピュータ・グラフィックスを駆使すれば、よい教科書が書けるに違いないと僕は思った。
本書で特に重要なキーワードを解説しているページと短い説明を書いておこう。
ブラベー格子： http://ceram.material.tohoku.ac.jp/~takamura/class/crystal/node7.html
格子は並進対称性と点対称性を持っている。対称操作（並進、回転、反転、鏡映）を施すことによって存在可能な格子は14種類である。この14種の格子を「ブラベー格子(Bravais Lattice)」と言う。ブラベー格子は、格子の点対称性に着目すると、7つの「結晶系」に分類することができる。
逆格子、逆格子ベクトル： http://ceram.material.tohoku.ac.jp/~takamura/class/crystal/node16.html
逆格子ベクトル（ぎゃくこうしべくとる、Reciprocal lattice vector）とは、物性物理における問題、特に結晶構造の解析やバンド計算等に用いる数学的な概念の一つで、波数の概念の一般化である。
ウイグナー-ザイツ・セル： http://www.f-denshi.com/000okite/300crstl/303cry.html
ウィグナー-ザイツ・セルとは、ある格子点と、その周りの格子点との間の垂直二等分面で囲まれた領域における最小のセル（胞）のことである。ユージン・ウィグナーとフレデリック・ザイツが名前の由来。ウイグナー-ザイツ・セルは、自動的にその結晶の基本単位格子となる。
ブリルアン・ゾーン： http://www.f-denshi.com/000okite/300crstl/306cry.html
ブリルアン・ゾーンとは逆格子におけるウィグナー-ザイツ・セルのことである（第１ブリルアン・ゾーン）。ある逆格子点の周りの逆格子点の垂直二等分面によって作られる領域は、無数にできるが、その中で最小の領域のことを第１ブリルアン・ゾーンという。それ以外は、第２ブリルアン・ゾーン、第３、、と称していく。ブリルアン・ゾーンは固体物理学において、波の散乱による回折条件を表現するために広く用いられている。これは、電子のエネルギーバンド理論などの説明に便利である。
ブロッホの定理： http://www.f-denshi.com/000okite/100ryosi/103free%20particle.html
物理学の法則の1つ。1928年に、フェリックス・ブロッホによって提出された。エネルギーバンドの計算をする場合に、結晶の並進対称性に関する重要な定理である。並進対称性とは、結晶が基本格子ベクトルだけ並進すると、自分自身と重なり合うことである。
この教科書で学んでみようという方は、こちらからどうぞ。
「固体物理の基礎 上・1 固体電子論概論： アシュクロフト、マーミン」- 1981
「固体物理の基礎 上・2 固体のバンド理論： アシュクロフト、マーミン」- 1981
「固体物理の基礎 下・1 固体フォノンの諸問題： アシュクロフト、マーミン」- 1981
「固体物理の基礎 下・2 固体の物性各論： アシュクロフト、マーミン」- 2008
Image may be NSFW.
Clik here to view.
Image may be NSFW.Clik here to view.
Image may be NSFW.Clik here to view.
Image may be NSFW.Clik here to view.
翻訳のもとになった英語版はこの本だ。
「Solid State Physics 1e: Neil W. Ashcroft, N.David Mermin」（ハードカバー）（ペーパーバック）
Image may be NSFW.
Clik here to view.
関連ページ： ネットで学びたい方はこちらからどうぞ。
目で見て操作する「分子の世界」－そのミクロ構造と物性－
http://rikanet2.jst.go.jp/contents/cp0200a/start.html
物性物理学（筑波大学物理学系 小野田雅重先生のページ）
http://www.px.tsukuba.ac.jp/~onoda/cmp/cmp.html
結晶回折学 講義資料
http://ceram.material.tohoku.ac.jp/~takamura/class/crystal/crystal.html
ときわ台学：物質・材料の掟 （公開版）
http://www.f-denshi.com/000okite/000matrl.html
関連記事：
物性物理30講（物理学30講シリーズ）：戸田盛和
http://blog.goo.ne.jp/ktonegaw/e/00d399f545bc69dfa213015f153a312a
基礎の固体物理学： 斯波弘行
http://blog.goo.ne.jp/ktonegaw/e/d2287a9fdbc66eac443fe0888d835602
応援クリックをお願いします！
Image may be NSFW.
Clik here to view.
Image may be NSFW.Clik here to view.
Image may be NSFW.Clik here to view.
Image may be NSFW.
Clik here to view.
Image may be NSFW.Clik here to view.
Image may be NSFW.
Clik here to view.
Image may be NSFW.Clik here to view.
「固体物理の基礎 上・1 固体電子論概論： アシュクロフト、マーミン」- 1981
Image may be NSFW.
Clik here to view.
第１章：金属のドゥルーデ（Drude）理論
- モデルの基礎仮定
- 衝突時間、緩和時間
- 直流電気伝導度
- ホール効果と磁気抵抗
- 交流電気伝導度
- 誘電関数とプラズマ共鳴
- 熱伝導度
- 熱電気効果
第２章：金属のゾンマーフェルト理論
- フェルミ・ディラック分布
- 自由電子
- 許された波数ベクトルの密度
- フェルミ運動量、フェルミ・エネルギー、フェルミ温度
- 基底状態エネルギーと体積弾性率
- 自由電子気体の熱的性質
- 伝導度のゾンマーフェルト理論
- ヴィーデマン・フランツの法則
第３章：自由電子モデルの破綻
- 自由電子モデルの困難
- 基礎仮定の復習
第４章：結晶格子
- ブラベー格子と基本ベクトル
- 単純立方格子と体心立方格子と面心立方格子
- 基本単位格子とウイグナー-ザイツ・セルと慣用単位格子
- 結晶構造と単位構造のある格子
- 六方最密構造とダイヤモンド構造
- 塩化ナトリウム構造と塩化セシウム構造とセン亜鉛鉱構造
第５章：逆格子
- 定義と例
- 第１ブリルアン・ゾーン
- 格子面とミラー指数
第６章：Ｘ線回折による結晶構造の決定
- ブラッグとフォン・ラウエの定式化
- ラウエの条件とエバルトの構成
- 実験方法：ラウエ法、回転結晶法、粉末法
- 結晶構造因子
- 原子形状因子
第７章：ブラベー格子の分類と結晶構造の分類
- 対称操作とブラベー格子の分類
- ７個の結晶系と１４個のブラベー格子
- 結晶点群と空間群
- シェーンフリース記号と国際記号
- 元素の例
第８章：周期ポテンシャル中の電子状態、一般的性質
- 周期ポテンシャルとブロッホの定理
- ボルン-フォン・カルマンの境界条件
- ブロッホの定理の第２の証明
- 結晶運動量、バンド指標、速度
- フェルミ面
- 状態密度とファン・ホーブの特異点
第９章：弱い周期ポテンシャルの中の電子
- 摂動論と弱い周期ポテンシャル
- 単一ブラッグ面近くのエネルギー状態
- １次元での拡張、還元、および周期ゾーン形式の説明
- フェルミ面とブリルアン・ゾーン
- 結晶構造因子
- スピン-軌道結合
第１０章：強く束縛された方法
- 原子軌道１結合
- s準位からのバンドへの応用
- 強く束縛された状態の一般的特徴
- ワニア関数
付録
Ａ：金属の自由電子論に出てくる重要な数値的関係式のまとめ
Ｂ：化学ポテンシャル
Ｃ：ゾンマーフェルト展開
Ｄ：１次元以上の周期関数の平面波展開
Ｅ：ブロッホ電子の速度と有効質量
Ｆ：周期系のフーリエ解析に関した恒等式
索引
その他の巻の章立て
上・２：固体のバンド理論
第１１章：バンド構造を計算する他の方法
第１２章：電子の動力学の半古典的モデル
第１３章：金属伝導の半古典的理論
第１４章：フェルミ面の測定
第１５章：いくつかの金属のバンド構造
第１６章：緩和時間近似を越えた近似
第１７章：独立電子近似を越えた近似
第１８章：表面効果
付録
下・１：固体フォノンの諸問題
第１９章：固体の分類
第２０章：凝集エネルギー
第２１章：静止格子模型の破綻
第２２章：調和結晶の古典論
第２３章：調和結晶の量子論
第２４章：フォノン分散関係の測定
第２５章：結晶の非調和効果
第２６章：金属中のフォノン
第２７章絶縁体の誘電的性質
付録
下・２：半導体、磁性体、超伝導体論
第２８章：均質な半導体
第２９章：不均質な半導体
第３０章：結晶中の欠陥
第３１章：反磁性と常磁性
第３２章：電子相互作用と磁気的構造
第３３章：磁気的秩序
第３４章：超伝導
付録