[Set 110,592 on Mr. Cube root]Zoom
[Japanese]
Following the last time, today's example is about actual solution of Cube root using abacus.
Today's example is simple - basic 1/3-multiplication table method, root is 2-digits case and we require root reduction in the steps. You can check the Index page of all articles.
Cube root methods: Triple-root method, constant number method, 3a^2 method, 1/3-division method, 1/3-multiplication table method, 1/3-multiplication table alternative method, Multiplication-Subtraction method, 3-root^2 method, Mixing method, Exceed number method, Omission Method, etc.
Abacus steps to solve Cube root of 110,592
(Answer is 48)
"1st group number" is the left most numbers in the 3-digits groups of the given number for cube root calculation. Number of groups is the number of digits of the Cube root.
110,592 -> (110|592): 110 is the 1st group number. The root digits is 2.
Image may be NSFW.
Clik here to view.
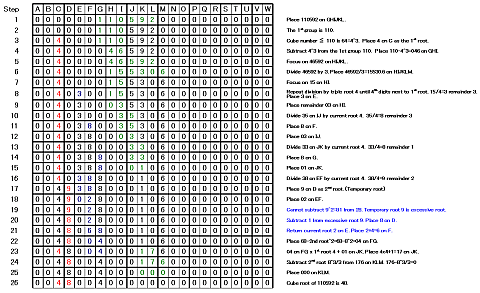
Step 1: Place 110592 on GHIJKL.
Image may be NSFW.
Clik here to view.
Step 2: The 1st group is 110.
Image may be NSFW.
Clik here to view.
Step 3: Cube number ≦ 110 is 64=4^3. Place 4 on C as the 1st root.
Image may be NSFW.
Clik here to view.
Step 4: Subtract 4^3 from the 1st group 110. Place 110-4^3=046 on GHI.
Image may be NSFW.
Clik here to view.
Step 5: Focus on 46592 on HIJKL.
Image may be NSFW.
Clik here to view.
Step 6: Divide 46592 by 3. Place 46592/3=15530.6 on HIJKLM.
Image may be NSFW.
Clik here to view.
Step 7: Focus on 15 on HI.
Image may be NSFW.
Clik here to view.
Step 8: Repeat division by triple root 4 until 4th digits next to 1st root. 15/4=3 remainder 3. Place 3 on E.
Image may be NSFW.
Clik here to view.
Step 9: Place remainder 03 on HI.
Image may be NSFW.
Clik here to view.
Step 10: Divide 35 on IJ by current root 4. 35/4=8 remainder 3
Image may be NSFW.
Clik here to view.
Step 11: Place 8 on F.
Image may be NSFW.
Clik here to view.
Step 12: Place 03 on IJ.
Image may be NSFW.
Clik here to view.
Step 13: Divide 33 on JK by current root 4. 33/4=8 remainder 1
Image may be NSFW.
Clik here to view.
Step 14: Place 8 on G.
Image may be NSFW.
Clik here to view.
Step 15: Place 01 on JK.
Image may be NSFW.
Clik here to view.
Step 16: Divide 38 on EF by current root 4. 38/4=9 remainder 2
Image may be NSFW.
Clik here to view.
Step 17: Place 9 on D as 2nd root. (Temporary root)
Image may be NSFW.
Clik here to view.![]()
Step 18: Place 02 on EF.
Image may be NSFW.
Clik here to view.![]()
Step 19: Cannot subtract 9^2=81 from 28. Temporary root 9 is excessive root.
Image may be NSFW.
Clik here to view.![]()
Step 20: Subtract 1 from excessive root 9. Place 8 on D.
Image may be NSFW.
Clik here to view.![]()
Step 21: Return current root 2 on E. Place 2+4=6 on F.
Image may be NSFW.
Clik here to view.![]()
Step 22: Place 68-2nd root^2=68-8^2=04 on FG.
Image may be NSFW.
Clik here to view.![]()
Step 23: 04 on FG x 1st root 4 + 01 on JK. Place 4x4+1=17 on JK.
Image may be NSFW.
Clik here to view.![]()
Step 24: Subtract 2nd root 8^3/3 from 176 on KLM. 176-8^3/3=0
Image may be NSFW.
Clik here to view.![]()
Step 25: Place 000 on KLM.
Image may be NSFW.
Clik here to view.![]()
Step 26: Cube root of 110592 is 48.
Image may be NSFW.
Clik here to view.![]()
Final state: Answer 48
Abacus state transition. (Click to Zoom)
Image may be NSFW.
Clik here to view.![]()
It is interesting to compare with the Triple-root method.
Next article is also 1/3-multiplication table method.
Related articles:
How to solve Cube root of 1729.03 using abacus? (Feynman v.s. Abacus man)
https://blog.goo.ne.jp/ktonegaw/e/cff5d6e7ecaa07230b9cc7af10b23aed
Index: Square root and Cube root using Abacus
https://blog.goo.ne.jp/ktonegaw/e/f62fb31b6a3a0417ec5d33591249451b
Cube root 110,592 using abacus (Triple-root method 3)
https://blog.goo.ne.jp/ktonegaw/e/ca623f02e6f5fdfef4221a5c43ea1a95
Please place your mouse on the buttons and click one by one. These are blog ranking sites.
Image may be NSFW.
Clik here to view.![にほんブログ村 科学ブログ 物理学へ]() Image may be NSFW.
Image may be NSFW.
Clik here to view.![人気ブログランキングへ]() Image may be NSFW.
Image may be NSFW.
Clik here to view.![]()
[Japanese]
Following the last time, today's example is about actual solution of Cube root using abacus.
Today's example is simple - basic 1/3-multiplication table method, root is 2-digits case and we require root reduction in the steps. You can check the Index page of all articles.
Cube root methods: Triple-root method, constant number method, 3a^2 method, 1/3-division method, 1/3-multiplication table method, 1/3-multiplication table alternative method, Multiplication-Subtraction method, 3-root^2 method, Mixing method, Exceed number method, Omission Method, etc.
Abacus steps to solve Cube root of 110,592
(Answer is 48)
"1st group number" is the left most numbers in the 3-digits groups of the given number for cube root calculation. Number of groups is the number of digits of the Cube root.
110,592 -> (110|592): 110 is the 1st group number. The root digits is 2.
Image may be NSFW.
Clik here to view.

Step 1: Place 110592 on GHIJKL.
Image may be NSFW.
Clik here to view.

Step 2: The 1st group is 110.
Image may be NSFW.
Clik here to view.

Step 3: Cube number ≦ 110 is 64=4^3. Place 4 on C as the 1st root.
Image may be NSFW.
Clik here to view.

Step 4: Subtract 4^3 from the 1st group 110. Place 110-4^3=046 on GHI.
Image may be NSFW.
Clik here to view.

Step 5: Focus on 46592 on HIJKL.
Image may be NSFW.
Clik here to view.

Step 6: Divide 46592 by 3. Place 46592/3=15530.6 on HIJKLM.
Image may be NSFW.
Clik here to view.

Step 7: Focus on 15 on HI.
Image may be NSFW.
Clik here to view.

Step 8: Repeat division by triple root 4 until 4th digits next to 1st root. 15/4=3 remainder 3. Place 3 on E.
Image may be NSFW.
Clik here to view.

Step 9: Place remainder 03 on HI.
Image may be NSFW.
Clik here to view.

Step 10: Divide 35 on IJ by current root 4. 35/4=8 remainder 3
Image may be NSFW.
Clik here to view.

Step 11: Place 8 on F.
Image may be NSFW.
Clik here to view.

Step 12: Place 03 on IJ.
Image may be NSFW.
Clik here to view.

Step 13: Divide 33 on JK by current root 4. 33/4=8 remainder 1
Image may be NSFW.
Clik here to view.

Step 14: Place 8 on G.
Image may be NSFW.
Clik here to view.

Step 15: Place 01 on JK.
Image may be NSFW.
Clik here to view.

Step 16: Divide 38 on EF by current root 4. 38/4=9 remainder 2
Image may be NSFW.
Clik here to view.

Step 17: Place 9 on D as 2nd root. (Temporary root)
Image may be NSFW.
Clik here to view.

Step 18: Place 02 on EF.
Image may be NSFW.
Clik here to view.

Step 19: Cannot subtract 9^2=81 from 28. Temporary root 9 is excessive root.
Image may be NSFW.
Clik here to view.

Step 20: Subtract 1 from excessive root 9. Place 8 on D.
Image may be NSFW.
Clik here to view.

Step 21: Return current root 2 on E. Place 2+4=6 on F.
Image may be NSFW.
Clik here to view.

Step 22: Place 68-2nd root^2=68-8^2=04 on FG.
Image may be NSFW.
Clik here to view.

Step 23: 04 on FG x 1st root 4 + 01 on JK. Place 4x4+1=17 on JK.
Image may be NSFW.
Clik here to view.

Step 24: Subtract 2nd root 8^3/3 from 176 on KLM. 176-8^3/3=0
Image may be NSFW.
Clik here to view.

Step 25: Place 000 on KLM.
Image may be NSFW.
Clik here to view.

Step 26: Cube root of 110592 is 48.
Image may be NSFW.
Clik here to view.

Final state: Answer 48
Abacus state transition. (Click to Zoom)
Image may be NSFW.
Clik here to view.
It is interesting to compare with the Triple-root method.
Next article is also 1/3-multiplication table method.
Related articles:
How to solve Cube root of 1729.03 using abacus? (Feynman v.s. Abacus man)
https://blog.goo.ne.jp/ktonegaw/e/cff5d6e7ecaa07230b9cc7af10b23aed
Index: Square root and Cube root using Abacus
https://blog.goo.ne.jp/ktonegaw/e/f62fb31b6a3a0417ec5d33591249451b
Cube root 110,592 using abacus (Triple-root method 3)
https://blog.goo.ne.jp/ktonegaw/e/ca623f02e6f5fdfef4221a5c43ea1a95
Please place your mouse on the buttons and click one by one. These are blog ranking sites.
Image may be NSFW.
Clik here to view.
 Image may be NSFW.
Image may be NSFW.Clik here to view.
 Image may be NSFW.
Image may be NSFW.Clik here to view.
