「数学する精神―正しさの創造、美しさの発見:加藤文元」(Kindle版)
内容紹介:
数学における「正しさ」とは何だろうか。数学の公式や証明と言えば絶対的に正しいもので、揺るぎない「神の知」だと思っている人も少なくないだろう。しかし数学を創ったのは紛れもなく人間であり、そうである以上、究極的には仮説的で暫定的であることを免れ得ない。ならば、多くの人が信じる「真の正しさ」や「美しさ」とは、数学という営みにおいてどんな意味を持つのか。拡がり続ける豊饒な数学の世界への招待。
2007年9月刊行、264ページ。
著者について:
加藤文元(かとうふみはる)
ホームページ: http://www.math.titech.ac.jp/~bungen/index-j.html
Twitter: @FumiharuKato
1968年生まれ。1997年京都大学大学院理学研究科数学専攻博士課程修了。熊本大学大学院自然科学研究科数学系教授。現在は東京工業大学理学院数学科系教授。専攻は代数幾何学・数論幾何学。著書『ガロア—天才数学者の生涯』『物語 数学の歴史—正しさへの挑戦』『数学する精神—正しさの創造、美しさの発見』(以上、中公新書)『数学の想像力―正しさの深層に何があるのか』(筑摩選書)など。
理数系書籍のレビュー記事は本書で316冊目。
加藤先生の著書は数年前から読みたいと思っていたのだが、ようやく読むことができた。6月には「現代思想 2016年3月臨時増刊号 総特集◎リーマン -リーマン予想のすべて-」の中の「討議」に参加されている加藤先生のリーマンの業績を読み、ますますその思いを強くしていた。
そして7月下旬と8月始めの2回に分けて行われた朝日カルチャーセンター新宿教室での加藤先生の講座に参加したかったのだが、入院中の家族の容態が急変してしまったため、申し込めなかった。(幸い奇跡的な回復を見せて、8月13日に無事退院することができた。)
せめて著書だけでも読んでおこうと通勤電車で読めるKindle本をということで、本書を選んだのである。加藤先生がお書きになった本の中ではいちばん古いものだと思う。
大学で数学を専攻していたし、「解析概論」も読破して理解している。また数学系の教養書も多数読んでいる。一般向けに書かれた数学書であっても面白い話、興味をそそる話はたくさんあり、今ではたいていの話は知っていて「またこの話か。」と思うことがよくあるものだ。とは言っても面白い話は好きなので、いつも貪欲に数学書を探し回り、新刊本は必ずチェックしている。
だから加藤先生には失礼だが書店で目次だけ読んだとき、あまり面白い本には思えなかった。ゼノンのパラドックスや数学的帰納法、二項展開、組み合わせの数、パスカルの三角形、二項定理など知っていることばかり並んでいたからだ。高校数学やり直し系の本ではないが、僕には易しすぎるのだろう。
しかし(面白さを期待せずに)読んでみると僕の予想は「良い意味で」全く外れてしまった。高校数学で学ぶ事柄だけで、こんなに奥深く、魅力的で不思議な数学の世界を引き出してくれるとは思いもしなかった。数学の教養書を数多く読んできた僕でも知らないことが(特に後半)書かれていた。数学の奥深さや魅力は大学以上の数学でしか味わえないと思っていたから、僕の常識は覆された。
章立ては次とおりだ。これだけではあまり内容が伝わらないから、詳細目次は記事の最後に書いておく。
はじめに
第1部:人間と数学
第1章:計算できる記号
第2章:ウサギとカメ
第3章:ビールのパラドックス
第4章:コンピュータと人間
間奏曲:数学の美しさ
トピックス:ベルンハルト・リーマン
第2部:記号と意味
第5章:組み合せの数
第6章:パスカルの半平面
第7章:ドッペルゲンガー
第8章:倒錯した数
第3章あたりまでは知っていることばかり。僕も同じように考えていたことばかりなので、普通に読み進んだ。初心者向けの本にもかかわらず「硬い」文章だ。先生は実直で誠実な方なのだなと思った。第1部の終わりのほうの「間奏曲:数学の美しさ」、「トピックス:ベルンハルト・リーマン」あたりから面白くなってきた。
第2部から山場が始まる。本書では「三位一体」という言葉であらわされている事柄なのだが、異なる3つの分野に不思議なつながりがあるということを意味している。昨年放送された「NHK数学ミステリー白熱教室」では「数論」、「調和解析」、「幾何学」(、そして「物理学」)の間の不思議なつながり(ラングランズ・プログラム=数学の大統一)が解説されたが、これは大学以上の数学の世界の話だ。
本書ではそのミニチュア版とでもいうべきつながりが「三位一体」として紹介される。

パスカルの三角形

二項展開(係数は組み合わせの数に等しい)

組み合わせの数
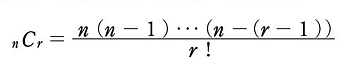
この3つの世界に対応関係があることは高校数学でも学ぶので、それほど目新しいことではない。
ところがである。この後、加藤先生は「パスカルの三角形の拡張」を2つの意味で行なってしまうのだ。拡張されたパスカルの三角形を本書では「パスカルの半平面」と呼んでいる。そうして拡張されたパスカルの三角形に対応する形で二項展開や組み合わせの数の世界にも新たな世界があらわれる。。。2つめの意味での拡張であらわれる世界を加藤先生は「ドッペルゲンガー」だとして解説されている。
新たな世界で私たちが見るドッペルゲンガーは思いがけない数や数式たちだ。それらは深く隠れたところまで拡がり、互いつながっている。私たちは生活の中で数を数えたり、量を測ったり、計算したりしているわけだが、私たちには別々のものに見えるそれらの数や数式は海面の上のところどころに突き出た氷山の一角のようなもので、本体は海面の下に深く広がり、つながっているのだと思い知らされる。
ここはとても興味深く、ワクワクすることなのでネタバレしないでおくことにしよう。ぜひ本書を読んで「驚いて」ほしい。
そしてもうひとつ印象に残ったのが「無限回の足し算の不思議」についてだ。「大栗先生の超弦理論入門」で次のような不思議な計算式が紹介されていたことは、多くの方がご存知だろう。これは1749年に大数学者オイラーが発表した式だ。

この式の証明を厳密に行うためには複素関数論で学ぶ解析接続という考え方が必要になる。この記事では高校レベルの厳密さを欠いた証明と、大学レベルの厳密な証明のページを紹介しておこう。
「1+2+3+4+…=-1/12」をわかったつもりになる
(高校数学レベルの解法、このページの「無理やり-1/12を導出する方法」という箇所)
http://nakaken88.com/2014/12/08/080818
なぜゼータ関数の自然数の和は無限大に発散しないのか?
(大学数学レベルの解法)
http://www.geocities.jp/x_seek/Euler.htm
本書には大栗先生の本やこの式、そして解析接続のことが書かれているわけではない。たまたま僕がこの記事に引用しただけである。
本書でとりあげられているのは、オイラーが発見した上の式はなく次の計算式だ。
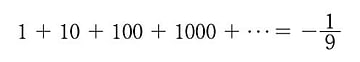
これもまた不思議な式である。高校数学で学ぶ「等比級数の和の公式」を当てはめることができるのだが、正の値を足し続けて負になるはずがない。
等比級数の和の公式

それに高校では公比 r の絶対値が1より小さいときに和の値は収束すると習った。この計算式の場合、公比 r は 10 である。すると右辺は確かに -1/9 になる。しかしこのような条件での計算に意味があるのだろうか?左辺は正の値だけなのだし。
「いったいどうして?」という謎は解析接続を使って解決することもできるが、本書ではずっと易しい手順で証明が与えられている。これもネタバレになるので、ここに書くのはやめておこう。
左辺の答を無限大とするのも正解だし、-1/12、-1/9とするのももうひとつの正解だ。後者を感覚的に受け入れられないのは、私たちが持っている数や計算の概念が数学の深いところにある本質に達していないことを象徴しているのだと思う。
2つの興味深い例を紹介したが、この2つ目の例も実を言うと1番目の例、つまり「パスカルの半平面」や「拡張版の二項定理」、「拡張版の組み合わせの数」と整合的なつながりを持つ形で成り立っているのだ。「ああ、素晴らしい!」と僕は感動してしまうわけである。
こうして僕が面白いところだけを切り取って紹介すると数学の雑学本のような印象を与えてしまうのだが、実際は具体例を積み上げていきながら、数学の思想の深いところでつながっている数の認識、記号表現などを解説し、「人間と数学の関わりの意味とは?」という深淵なテーマにまで掘り下げている本なのだ。加藤先生は次のようにお書きになっている。
数学における「正しさ」とは何だろうか。数学の公式や証明と言えば絶対的に正しいもので、揺るぎない「神の知」だと思っている人も少なくないだろう。しかし数学を創ったのは紛れもなく人間であり、そうである以上、究極的には仮説的で暫定的であることを免れ得ない。ならば、多くの人が信じる「真の正しさ」や「美しさ」とは、数学という営みにおいてどんな意味を持つのか。拡がり続ける豊饒な数学の世界への招待。
高校数学で学ぶ内容だけで、これほど深い世界を見せてくれる本は僕にとっても初めてである。これが本書の最大の魅力だ。
加藤先生のご専門である代数幾何学に通じる「p進数」のことは最終章で取り上げられているが、この部分は説明が足りないと感じた。
「p進数」については、9月20日に発売される次の本をお読みになるとよいだろう。初等整数論への入門書である。目次は日本評論社HPのこのページに掲載されている。
「天に向かって続く数:加藤文元、中井保行」

その他、加藤先生がお書きになった本は、以下のリンクからご覧いただだきたい。
加藤先生の著書: Amazonで検索
お知らせ:
今日紹介した本の内容をテーマにした加藤先生の講座が10月から月1回(計6回)行われるそうだ。東京近郊で興味のある方はどうぞ。
朝日カルチャーセンター(新宿教室): 一般会員 ユース学生会員
【新設】数学・人間・記号
「数学する精神」への招待
講師:東京工業大学教授 加藤文元
講座内容:
数学はとても抽象的な学問で、それだけに非人間的な印象を受けることもあるでしょう。しかし、数学も人間がつくったものであり、それだけに人間の人間たるゆえんがいたるところに見出せる学問です。数学を学ぶことは人間を学ぶことです。また他方、数学の高い抽象性の根幹には、広大な「記号」の沃野があります。記号に意味を吹き込むのは人間ですが、記号の天真爛漫な振る舞いから思いがけない数学が生まれることもあります。数学・人間、そして記号という三者の間の弁証法から様々に豊かな数学が生まれる過程を、拙著『数学する精神』を通して見ていきたいと思います。(講師・記)
<講座スケジュール>
110月11日人間と数学(その1) 「アキレスと亀」を巡って
211月 8日人間と数学(その2) 数学的帰納法の認識論
312月13日人間と数学(その3) パスカルの半平面
日時・期間:第2週 火曜 19:00-20:30 10/11~12/13 3回
ブログ執筆のはげみになりますので、1つずつ応援クリックをお願いします。



とね日記は長年放置されている科学ブログランキングの不正クリックに対し、次のランキングサイトには適切な運営を期待します。
「人気ブログランキング(科学)」、New!-「人気ブログランキング(物理学)」、「FC2自然科学ブログランキング」:不正の例1 例2 例3(クリックしてからTwitterアプリで開くと画像は鮮明に見れます。)
(不正クリックブログの見分け方)




「数学する精神―正しさの創造、美しさの発見:加藤文元」(Kindle版)

はじめに
- 人間と数学 記号と意味
第1部:人間と数学
第1章:計算できる記号
- 自然の中の数
- 数の二面性
- 「見よ!」
- 解説:ユークリッド幾何学
- 代数学
- 0の発見
- 演算規則
- 二項展開
- 計算できる記号
- 人間と数学
トピックス:数学の記号化と公理的数学
第2章:ウサギとカメ
- ゼノンのパラドックス
- 勝負の判定は?
- 等比級数の和
- 「連続」の難しさ
- 解説:有理数と実数
- 「モデル」としての実数論
- 実数論の「仮説的」側面
- 実数論の二つのポイント
トピックス:非ユークリッド幾何学
第3章:ビールのパラドックス
- 何杯飲めるか
- 積のべきとべきの積
- どこまでできるか
- ビールのパラドックス
- 数学的帰納法
- 常識的な見方
- 「公理系」の中の数学的帰納法
- 集合論の中の数学的帰納法
トピックス:集合論と失楽園
第4章:コンピュータと人間
- 我思う故に我あり
- メタな自分
- 不完全性とコギト
- パスカルの三角形
- 二項展開
- ずらし算
- 二項定理
- パターンの比較
- ちょっと歴史
間奏曲:数学の美しさ
トピックス:ベルンハルト・リーマン
第2部:記号と意味
第5章:組み合せの数
- テストの正解率
- 10個から3個選ぶ
- コンビネーション
- 計算例
- 禅問答
- 三角数と平方数
- コンビネーションの「パターン」
- 三位一体
トピックス:リーマンの三位一体
第6章:パスカルの半平面
- 二項定理の「ホラ」
- 失われた上半分
- パスカルの半平面
- ライプニッツ記号
- 二項定理との整合性
- 等比級数の和ふたたび
- 無限ずらし算
- 負のべきも許した二項定理
第7章:ドッペルゲンガー
- 無理数の発見
- 解説:√2の無理性
- ドッペルゲンガーの怪
- ライプニッツ記号に分数を入れる
- 分数べきの計算
- √2の計算
トピックス:円周率の計算
- 圧倒する影
第8章:倒錯した数
- 倒錯した世界
- 禁則破り
- 10進展開
- 状況証拠
- 仮説的な「距離」の概念
- 10進距離による「近似」
- p進数
- 「猫」の目
エピローグ:数の系譜
あとがき
主要参考文献