「とねさんはついに一線を越えてしまったようだ。」という声が聞こえてきそうだが、そうではない。僕が興味をもったのはストッキングではなく極小曲面、最小面積曲面のほうだ。
話の発端は6年前にさかのぼる。「"5" で現れる不思議な形 (フェルマー点の話)」という記事でシャボン液の表面張力によってつくられる不思議な形のことを紹介した。この記事では2次元のシャボン液の膜による現象を扱ったわけだが、見える形としては膜を横から見た1次元の「線」の話である。
ネットで調べると立体的に作った針金の枠をシャボン液に浸して作る面白そうな実験がいくつか見つかった。なるほど、シャボン液の膜は表面張力によって3次元の空間の中でも面積が最小になるように張るのか。これは面白そうだ。僕もやってみたい。次のページを見れば、僕の気持がわかるだろう。
みんなの実験室14:**三角四角のしゃぼん玉?**
http://www2.tokai.or.jp/seed/seed/minnna14.htm
特に次の例には興味をひかれた。左がシャボン膜の面積が「最小」になっているケースで、右は面積が「極小」になっているケースだという。最小と極小の違いとは何だろうか?

2次元の場合だと6年前に僕の記事で図示した次のケースに対応する。この3次元版が上の左側の状況に対応するのだ。
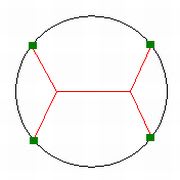
でも同じことをやったのでは能がない。そして思いついたのがストッキングだ。シャボン液のときと同じ結果が得られるだろうか?それともまた違った結果になるのだろうか?
とはいえ自分で買う勇気はない。そこで「知り合い以上、友達未満」のマキちゃん(25歳の女子)に事情を説明してお願いした。そして2週間くらいたってから受け取ったのがセブンイレブンで買ったというベージュ色のストッキング。(記事トップの写真)
事情を説明するのはとても大切だ。さもなければ変態と勘違いされて「知り合い未満」に格下げになる。
念願のストッキングが手に入ったのでさっそく実験開始。
まずやってみたのがこれ。針金でできたハンガーを四角になるように折り曲げてにストッキングをかぶせてみた。

蝿たたきのようにストッキングは平面に張る。あらゆる方向に均等な張力が働いた結果、面積は最小になっていることもわかりやすい。
次に試してみたいのが乗馬で使う鞍のようなこの形。数学的には曲率(正しく言えば「ガウス曲率」)がマイナスになるケース。

曲率についてだが1次元、つまり曲線のときはわかりやすい。たとえば放物線を例にとって言えば、下に凸の放物線は曲率がプラス、上に凸の放物線は曲率がマイナス。そして曲率がゼロのときは「直線」になる。曲率の正負は放物線の方程式の係数 a の正負に一致するように決めておこう。

ところが2次元、つまり曲面の曲率はもう少し複雑だ。上の馬の鞍のような形は縦方向は上に凸で、横方向は下に凸。このとき曲率(ガウス曲率)はマイナスになる。ガウス曲率は縦方向の曲率と横方向の曲率の積(掛け算)で計算するのでマイナスxプラス=マイナスというのがその理由だ。
ガウス曲率 = 縦方向の曲率 x 横方向の曲率
そして針金をそのように曲げて作ってみたのが馬の鞍の形。針金を縦方向と横方向逆に曲げて作る。方向を変えてとりあえず3枚。



理由は後で述べるが、この曲面は最小面積になっているのだ。面の周囲が曲がった針金の枠に固定された条件で、面の内側のすべての点で張力が縦方向、横方向均等につりあっている状態である。
曲面の場合、曲率にはいくつかの種類がある。上で述べたガウス曲率の次に説明するのが「平均曲率」というものだ。平均曲率は縦方向の曲率と横方向の曲率の平均(縦曲率と横曲率を足して2で割る)で計算する。この乗馬の鞍の場合はプラスとマイナスがちょうど差し引きされてゼロになる。
平均曲率 = (縦方向の曲率 + 横方向の曲率)÷2
つまり、このような2つの曲面についてガウス曲率と平均曲率が計算できる。

赤線を縦方向、黒線を横方向とみなすことにすれば次のようになる。
左の曲面のガウス曲率=マイナスxマイナス=プラス
左の曲面の平均曲率 =(マイナス+マイナス)÷2=マイナス
右の曲面のガウス曲率=マイナスxプラス=マイナス
右の曲面の平均曲率 =(マイナス+プラス)÷2=ゼロ
そして次の「3次元ユークリッド空間内の極小曲面」というページを見ると冒頭には次のように書かれている。『平均曲率が曲面上のいたるところで0となる曲面を極小曲面と呼びます。 ワイヤーフレームに張る石けん膜は表面張力により面積が極小になります。 この面積極小という性質を変分法によって定式化すると、「面積が極小ならば平均曲率が0となる」ことが示されます。 』
3次元ユークリッド空間内の極小曲面
http://www.comp.tmu.ac.jp/tsakai/lectures/soron2010.html
僕が面白いと思うのは外との境界になる枠の形が決まれば、枠の中の曲面の形が1通りに決まるということだ。外枠を変形させれば曲面の形もそれに応じて変化する。
実をいうとこれは一般的にすべての次元について成り立っているのだ。たとえば次の写真は「光弾性を使った力の教材化」というページから借用した透明なスーパーボールなのだが、ボールの境界面(球の表面)に力を加えて内部の歪みを視覚化している。境界面に加える力の位置や方向、大きさに応じて、立体的な内部の圧力はその方向も含めてあらゆる場所で1通りに決まる。

外側の境界条件を決めれば内部すべての状況が決まってしまう。たとえ次元の数が違っていても数学的には同じことなのだ。ひもの境界は両方の端点であり、面の境界は外周であり、立体の境界はその表面全体である。4次元以上でも同じこと。そこにはあらゆる次元で成り立つ1つの定理が存在しているのだ。
ともかく乗馬の鞍形にストッキングを張ると面積は「極小」になっているわけだな。それじゃ「最小」と「極小」はどうやって区別すればよいのだろう?
疑問はそのままにしておいて、次の形で試してみることにした。CDやDVDを50枚まとめて買うと、このような物体を手に入れることができる。

これにストッキングをかぶせれば、面積が最小か極小になると思われるから、円錐のような形があらわれるだろうか?なぜなら柱のてっぺんと下の円周を結ぶ最短距離は直線になり、それは円錐の側面の直線(これを母線と呼んでいる)になりそうだから。
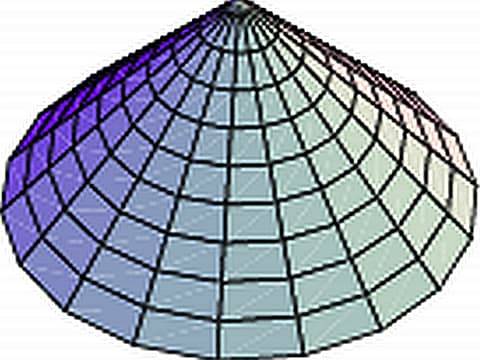
ところがやってみると次のようになった。容易に想像できた形なのだが、実際にやってみると美しい曲面があらわれたので、しばらく鑑賞してしまった。そしてこの形はシャボン膜では容易に作れない。

真横から見ると、斜面には何かの数式であらわせそうな曲線があらわれている。

はたしてこれは面積最小になっているのだろうか?それとも極小?理由はさらに後に持ち越すが、これで面積最小になっているのだ。
でも、もしかしたらストッキングをもっと強く張って、つまり下のほうを強く絞ったら形は円錐に近づくのだろうか?そして最大限強く張ったらほとんど円錐になるのだろうか?
やってみたのだが、形はほとんど変わらなかった。相変わらず「富士山型」の美しい曲面のままだった。この富士山型も平均曲率はゼロなので「極小曲面」になっている。
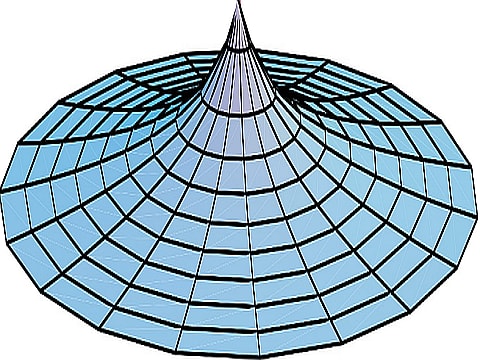
これは数学的に何か名前のついている曲面なのだろうか?
そして次に気になったのがこのような鼓(つづみ)の形。さきほどの「3次元ユークリッド空間内の極小曲面」というページによるとこれも平均曲率はゼロだから極小曲面のひとつで「懸垂面」という名前がつけられている。
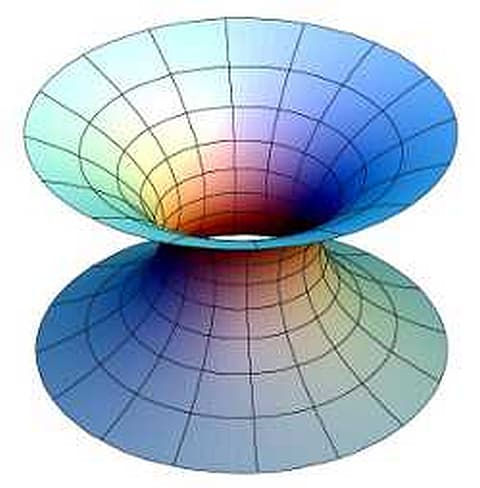
この形をストッキングで作るためには上と下で同じ半径の円盤を用意しなければならない。
しばらく考えた末、先日買った「ちびくろちゃん 2号炊き」のフタがちょうどよい具合に使えることに気がついた。

そして出来上がったのがこの曲面。円柱にはならなかった。ストッキングを強く張ってもこの曲面はくずれずに安定している。極小曲面の完成だ。

そして僕が次に見つけたのがこのPDF文書。
曲面の変分問題(極小曲面論入門)
http://www.jst.go.jp/crest/math/ja/suugakujuku/archive/text/3_Koiso_text.pdf
数式がたくさん書いてあり、とても難しいのだが12ページ目にこのような図を発見。

そうか、「極小曲面」には安定なものと不安定なものがあるわけか。そしてPDF文書内のこの図のすぐ上に「物理的に実現される極小曲面は安定なものだけであると言ってよい。したがって、極小曲面のうちで安定なものとそうでない(不安定な) ものとを区別することは自然である。」という説明がある。
つまり数学的には極小曲面はいくつもあるが、そのうち物理現象として実現するのはただ1つで最小面積曲面になっているというわけか。そうすると、これまでストッキングを使って作った曲面は、ぜんぶ物理的に安定したものだから面積が最小になっているということになる。集合の包含関係で示せば次のようになる。
(数学的な)極小面積曲面 ⊃ (物理的な)最小面積曲面
「懸垂」というのがキーワードだ。ひもや鎖をだらんと垂らしてできる曲線のことを「懸垂線」と呼んでいる。

懸垂線を関数として求め、そのグラフを描いてみたい。これは「変分法」というのを使って解く問題で、次のページのようにして求めることができる。
懸垂線(変分法を使って解く)
http://analytical-mechanics.matrix.jp/catenary.html
その結果、次のように懸垂線の数式とグラフを得ることができた。

上の変分法のページには懸垂面の図が描かれていることにお気づきだったろうか? そう、懸垂線を中心軸のまわりに回転させると懸垂面ができあがるのだ。厳密なことを言えば懸垂面についても変分法を使って極小曲面を導かなければいけないわけだが、難度が高すぎるので今回は省略させていただく。
ところで「富士山型」の最小面積曲面なのだが、この上に同じ富士山を逆さまにしてつなげるとこのような形になる。

実はこれも懸垂面なのだ。中心が極端に絞られているとはいえ、物理的には安定している。富士山型の最小面積曲面はこの形の下半分だったというわけ。
ひもや鎖を垂らしてできる懸垂線は、自分自身の重さでそのような形に垂れるわけだが、懸垂面のほうは面の表面張力によってそのような形の面が形成される。両者の力学的メカニズムは全く違うのに同じタイプの数式であらわされる曲線が出てくるというのはとても興味深い。
ほかにもいくつかの形で試してみた。以下はすべて最小面積曲面である。数学的な曲面の美を堪能していただきたい。








この最後の例なのだが、みなさんはお気づきだろうか? 傘の布地は骨と骨の間が少しへこんでいる。これはデザインのためにそういう形にしているのではない。これも最小面積曲面になっているからなのだ。

極小曲面で「面積が極小ならば平均曲率が0となる」ということの証明は、昨年T_NAKAさんがブログ記事をお書きになっているので(理数系大学生の方は)お読みになっていただきたい。
いろいろな曲面(2)_ b )極小曲面
http://teenaka.at.webry.info/201308/article_21.html
曲線や曲面の数学は曲線論・曲面論と呼ばれていて、微分幾何学の分野のひとつだ。微分幾何学を創始したのはアイザック・ニュートンで、曲面論は1800年代から大数学者ガウスをはじめ、多くの数学者によって研究された。
ガウスの弟子のひとりであるレオンハルト・リーマンは後に曲面論を多次元(N次元)に一般化させ、1867年に「リーマン幾何学」を発表した。そしておよそ50年後、リーマンの曲がった多次元空間の幾何学を4次元の曲がった時空に使うことでアインシュタインは一般相対性理論を発表することができたのだ。
幾何学の基礎をなす仮説について:ベルンハルト・リーマン
http://blog.goo.ne.jp/ktonegaw/e/22be602fe4cee385a9939c0869c511eb
時空の幾何学:特殊および一般相対論の数学的基礎
http://blog.goo.ne.jp/ktonegaw/e/ffc643a688ce45dec7460d107fe1392e
一般相対性理論に挑戦しよう!
http://blog.goo.ne.jp/ktonegaw/e/ea7ad9292ce01ad4abbbc8c98f3303d0
曲線や曲面の数学的性質について学びたい方は、次の名著をお勧めしたい。(ただし高校生には難しすぎるので無理。)第5章が極小曲面の解説にあてられている。
「曲線と曲面の微分幾何(増補版): 小林昭七著」(紹介記事)

中学生や高校生にとって夏休みはもうすぐだ。自由研究にストッキングを使ったこの実験をしてみようかと思った人もいるかもしれない。
でもそれはやめたほうがよい。なぜなら「極小曲面」や「最小面積曲面」という日常的に使わない数学用語は友達や兄弟には覚えにくい言葉なので、あなたの知らないうちに抜け落ちてしまい「〜クンはストッキングの研究をしているようだ。」とか「〜クンはストッキングをたくさん集めているらしい。」という感じで噂が広まっていくことだろうから。
いちど貼られた変態のレッテルをはがすのは容易なことではない。
そのようなリスクを覚悟の上で実験をしてみたいという人は、こちらからどうぞ。
「きれいに魅せるオールスルーサポートパンティストッキング(パンスト)3足セット」

今回の話のオチはこの写真。ストッキングをかぶせた多数のマネキン。これらも最小面積曲面になっていて、このページから拝借させていただいた。

応援クリックをお願いします!



